快慢指针算

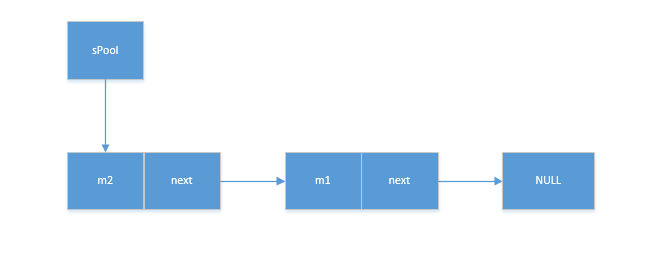
快慢指针算法，多用于链表当中，常见的如：快慢指针判断链表中是否含有环路&&快慢指针找链表中点问题

力扣141. 环形链表

题目链接：141. 环形链表
在这里插入图片描述

思路

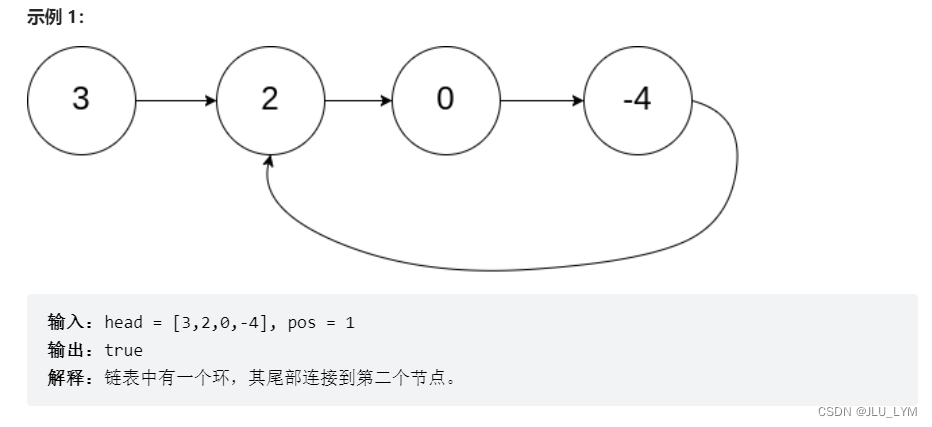
这是非常经典的，Floyd判圈法，即利用快慢指针，判断链表中是否含有环路。

1、初始时，slow、fast都在开头节点
2、fast一次走两步，slow一次走一步
3、如果含有环路，二者一定在环路中相遇；反之fast先走到尾节点

代码

class Solution {
public:
	bool hasCycle(ListNode *head) {
		ListNode *slow = head, *fast = head;
		while (fast != nullptr&&fast->next != nullptr) {//快慢指针判断条件！！！
			slow = slow->next;
			fast = fast->next->next;
			if (slow == fast) {
				return true;
			}
		}
		return false;
	}
};

力扣142. 环形链表 II

题目链接：142. 环形链表 II
在这里插入图片描述

思路

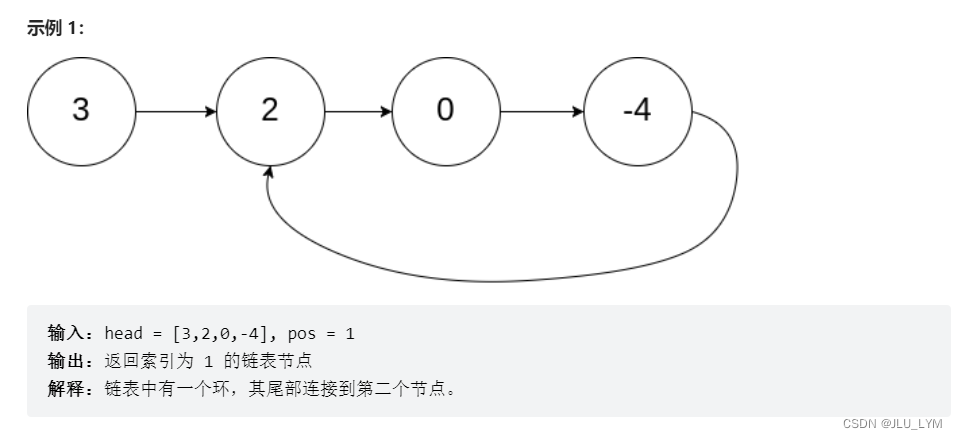
本题为上一题的进阶版本，我们不仅要判断是否含有环路，还要判断环路的进入节点，并返回。
1、所以，我们第一步就是利用快慢指针，利用是否会有第一次相遇，判断出是否含有环路，思路同上一题。
2、当相遇时，二者处在环路中某一个节点，现在我们要通过分析快慢指针走过的步数，来进一步指定算法

1、设非环路部分链表共a个节点，环路部分链表共b个节点(a,b均未知，具体要看题目)
2、我们从头部出发，到达环路入口节点：要么直接走过去，即a步；要么走入环路，在环路中绕行整数个圈到达。综上，总步数为 a+nb（n为绕行圈数，为未知，看具体链表）
3、再来分析快慢指针已经走了多少步：分别设为f、s步
<1>f=2s（快指针一次两步，慢指针一次一步）
<2>f=s+nb（快慢指针都同样走过了a步，快指针多比慢指针在环路中走了几圈，且n为未知）
所以f=2nb、s=nb
4、在当下，慢指针已经走了nb步，根据上面分析，再走a步就是目标节点。但是，现在a是未知，根据上面分析，我直接从起点走a步也会到目标点。
5、综上，让快指针去链表头，让快慢指针同时按照一个速度出发，二者相遇的时候，同时走了a步，即为目标点

代码

class Solution {
public:
	ListNode *detectCycle(ListNode *head) {
		ListNode *slow = head, *fast = head;
		while (fast != nullptr&&fast->next != nullptr) {//快慢指针判断条件
			slow = slow->next;
			fast = fast->next->next;
			if (slow == fast) {//产生第一次相遇，证明含有环路，开始寻找目标点
				fast = head;//这里算法详见上面证明
				while (fast != slow) {
					fast = fast->next;
					slow = slow->next;
				}
				return slow;
			}
		}
		return nullptr;//不产生第一次相遇，不含有环路
	}
};

滑动窗口

1、滑动窗口，又名双指针法，左右两个指针（l,r），同方向且l<=r，用于区间搜索。
2、只要分析出滑动窗口法之后，马上想到滑窗固定大板子：

1、滑窗之中，一定要重点统计窗口内部数据情况，这个和窗口是否收缩有很大关系
2、总体思路就是，先进行右边界扩张，更新窗口内数据信息；再根据题意判断，是否左边界++，进行窗口收缩，收缩的话，一定注意更新窗口内数据信息
3、左右指针初始化为 0 -1

	int left = 0, right = -1;
 	for (遍历一遍数组) {
		// c 是将移入窗口的字符
   	 	char c = s[right];
    	// 右移窗口
    	right++;
    	// 进行窗口内数据的一系列更新
    	...   
    	// 判断左侧窗口是否要收缩
    	while (左指针需要移动，即窗口需要收缩) {
        	// d 是将移出窗口的字符
        	char d = s[left];
        	// 左移窗口
        	left++;
        	// 进行窗口内数据的一系列更新
        	...
    	}

力扣76. 最小覆盖子串

题目链接：76. 最小覆盖子串
在这里插入图片描述

思路

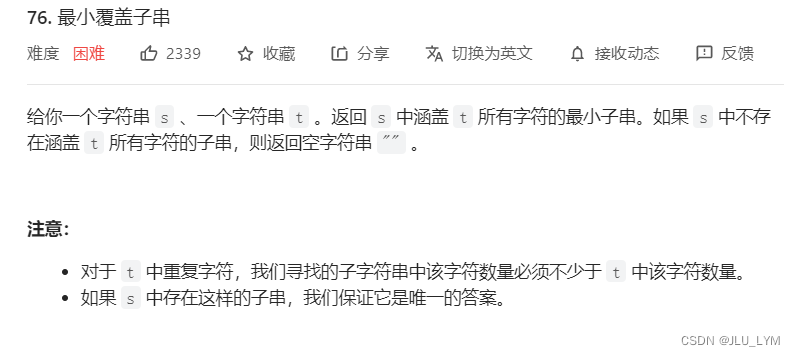
本题要求我们在s中找一个片段，这个片段中必须包含t中全部出现的字母，即t中出现了2个a，那么目标片段必须出现2个a，且要求在所有满足要求的片段之中找到最短的(根据题意，答案一定唯一)，这明显是区间搜索问题，马上想到滑窗法，立刻开始套模板

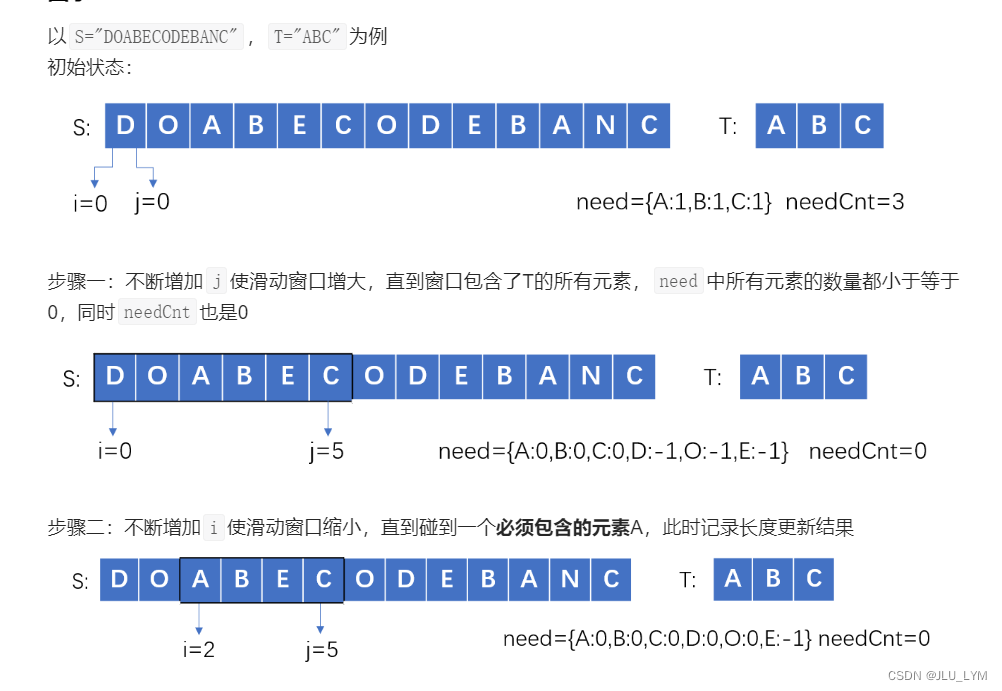
1、初始化 l=0,r=-1，针对滑窗，我们要统计滑窗内各个元素出现的个数，针对t，我们要统计出现了哪些元素，以及出现的次数。
2、每次先右边界++，扩充滑窗，更新滑窗内元素。
3、最重要的地方来了，如何判断是否缩小滑窗(即左边界++)：如果当前滑窗内都为覆盖到所有目标元素，那么缩小滑窗之后，更是不可能覆盖。所以只有当扩充玩新元素后全覆盖到了，才考虑缩小滑窗。
4、为了看是否能达到覆盖，用sum记录还需要覆盖的字母总量，用tmp数组动态维护需要覆盖的各个字母剩余数量。
5、根据题意，当能覆盖之后，我们要这个片段尽可能的短，所以在缩小滑窗时候，当恰好排出这个元素之后，无法完全覆盖，这就代表着不缩小时，就是当前的满足要求的最短片段。所以，我们连续缩小滑窗，直到上述情况出现即可。为了让最终结果最小，要动态维护一个最短片段。

在这里插入图片描述

代码

注意：
1、字符串裁剪函数substr使用方式：
假设：string s = “0123456789”;
string sub1 = s.substr(5); //只有一个数字5表示从下标为5开始一直到结尾：sub1 = “56789”
string sub2 = s.substr(5, 3); //从下标为5开始截取长度为3位：sub2 = “567”
2、比如t串中只出现两个a,但窗口内出现了三个a，只有前两个算有效覆盖(既在t中出现，又满足出现次数)，所以tmp就是用来动态维护这个事情

class Solution {
public:
	string minWindow(string s, string t) {
		int m = s.size(), n = t.size();
		//统计字符串t里面的字符信息
		vector<int> cnt1(128, 0);//统计t中各个字母出现的次数
		vector<bool> visit1(128, false);//看t中出现了哪些字母
		for (int i = 0; i < n; i++) {
			cnt1[t[i]]++;
			visit1[t[i]] = true;
		}
		
		//用来动态记录最短符合要求字串
		int min_l = -1, min_r = -1, mins = 1000001;//左边界，右边界，长度
		
		int l = 0, r = -1;//窗口左右指针
		int sum = n;//还未覆盖到的字母总数
		vector<int> tmp(cnt1);//复制一下cnt1，动态维护一下窗口内还需要覆盖的各个字母的个数
		vector<int> cnt2(128, 0);//维护窗口内所有元素出现的次数
		
		for (int i = 0; i < m; i++) {
			char tar = s[i];//待扩充进来的字符
			r++;//扩充右边界
			cnt2[tar]++;//更新窗口内元素出现次数
			//扩充进来的字母是有效的覆盖，解释看上面的注意部分
			if (visit1[tar] == true && tmp[tar] != 0) {
				sum--;//要覆盖的总数-1
				tmp[tar]--;//窗口内该字母还需要出现的次数-1
			}
			//开始判断是否要缩减窗口
			if (sum == 0) {//刚刚好，窗口扩展到全覆盖时候，才开始动左指针，找到当前状态下最小
				//当前窗口完全可以覆盖，为了找最小，我们收缩左边界，直到恰好覆盖(即再缩就不可以覆盖为止)
				//这时候，就是当前状态下最小
				while (sum == 0) {//连续缩小
					char tar2 = s[l];//待排除的元素
					if (visit1[tar2] == true) {//被扔出去的字母是有效字母,反之直接扔即可(l++)
						cnt2[tar2]--;//动态维护窗口内各字母个数，有效字母被扔出去后，它的新数量
						if (cnt2[tar2] < cnt1[tar2]) {//当前窗口不能恰好覆盖目标字母，这个时候就是连续缩窗口的尽头，开始更新动态维护的数据
							sum++;//窗口内待覆盖的元素+1
							if (r - l + 1 < mins) {//动态维护最小子串
								mins = r - l + 1;
								min_l = l;
								min_r = r;
							}
							tmp[tar2]++;//该字母在窗口内还需出现的次数+1
							l++;//缩窗口
							break;//退出连续缩窗口
						}
					}
					l++;
				}
			}
		}
		return min_l == -1 ? "" : s.substr(min_l, min_r-min_l+1);//始终未找到合适的窗口，min_l==-1，返回空串；反之按照大小裁剪目标串s
	}
};

力扣424. 替换后的最长重复字符

题目链接424. 替换后的最长重复字符
在这里插入图片描述

思路

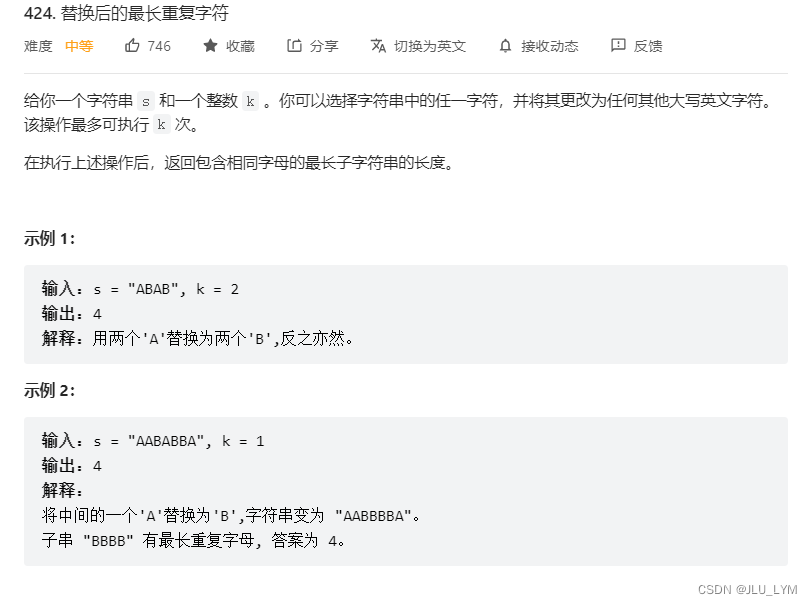
明显的，在大区间中，找一个连续的小区间，经过不多于k次的变化之后，让其中元素都统一，且这个片段要最长。区间搜索，马上想滑窗，上模板：

1、初始化 l=0 ；r=-1 ；统计窗口内各个元素个数；一个窗口内，为了在有限的替换之后，整体最长，肯定是维护一个个数最多的元素，把和他不同的全换下去，这样才会最长，也能最大程度上利用k,所以维护窗口内最大元素个数
2、r++，扩充窗口，更新元素数量，因为该字母变多了，可能成为最多的个数，所以也要维护窗口内最大元素个数
3、滑窗问题关键来了，缩小窗口：当”非最多数量元素“个数小于等于k（可替换数量），说明这次扩充是可以的，窗口确实可以扩张，不需要收缩（因为题目要的就是最长），反之，就得收缩，更新的数据同上

代码

class Solution {
public:
	int characterReplacement(string s, int k) {
		int n = s.size();
		vector<int> cnt(26, 0);//窗口各个字母个数
		int l = 0, r = -1;
		int maxs = 0;
		for (int i = 0; i < n; i++) {
			char tar = s[i];//待扩充元素
			r++;//扩充
			cnt[tar - 'A']++;//两次更新数据
			maxs = max(maxs, cnt[tar - 'A']);
			if (r - l + 1 - maxs > k) {//扩充失败了，必须要收缩一下
				char tmp = s[l];
				cnt[tmp - 'A']--;
				for (int j = 0; j < 26; j++) {
					maxs = max(maxs, cnt[j]);
				}
				l++;
			}
		}
		return r - l + 1;
	}
};