webrtc QOS笔记一 Neteq直方图算法浅读

Histogram Algorithm

DelayManager::Update()->Histogram::Add() 会根据计算的iat_packet(inter arrival times, =实际包间间隔 / 打包时长)，将该iat_packet插入IATVector直方图对应数组下标内。并更新该直方图的数据下标下概率参数。[M88 SRC]

一共有四步操作：

1、用遗忘因子，对历史数据的出现概率进行遗忘, 并统计概率合
$buckets\_[i]=buckets\_[i]\ast forget\_factor$

$vector\_sum={\sum }_0^{buckets.size()}buckets\_[i]\ast forget\_factor$

2、增大本次计算到的IAT的概率值。

$buckets\_[value]=buckets\_[value]+(1-forge{t}_{f}actor\_)$

$vector\_sum=vector\_sum+(1-forget\_factor\_)$

• 例：

假如历史bucket 数据为:
buckets_ = {0，0，1，0}

遗忘因子为 0.9:
forget_factor = 0.9

新来的抖动延迟数据为66ms， 桶间为20ms一个单位, 那插入位置为 66 / 20 = 3，则更新后

buckets = {0，0，0.9，0.1}

假若使用%95分位的值作为目标延迟， 则更新后的目标延迟为 60ms.

3、调整本次计算到的IAT的概率，使整个IAT的概率分布之和近似为1。调整方式为假设当前概率分布之和为tempSum，则：

$vecto{r}_{s}um=1-vecto{r}_{s}um$

$$bucket{s}_{[}n]=\{\begin{array}{l}buckets\_[n]-Min(\mid vector\_sum\mid ,buckets\_[n]/16)if(vecto{r}_{s}um>0)\\ buckets\_[n]+Min(\mid vector\_sum\mid ,buckets\_[n]/16)if(vecto{r}_{s}um>0)\end{array}$$

4、更新forget_factor_, 使遗忘因子forget_factor_逼近base_forget_factor_

a.使用start_forget_weight_更新(默认初始值start_forget_weight_ = 2，base_forget_factor_=0.9993)

$add\_count\_++$
$forget\_factor\_=1-(start\_forget\_weight\_/(add\_count\_+1))$
$forget\_factor\_=Max(0,Min(base\_forget\_factor\_,forget\_factor))$

b. 其中的3是Q30的值，没有多大 = 0.000091552734375
$forget\_factor\_=forge{t}_{f}actor\_+(base\_forget\_factor\_-forget\_factor\_+3)/4$

获取目标延迟

依据probability获取此百分位的值作为目标延迟(初始值0.97)

${\sum }_0^{n}buckets\_[n]>probability$

int Histogram::Quantile(int probability) {
  // Find the bucket for which the probability of observing an
  // inter-arrival time larger than or equal to |index| is larger than or
  // equal to |probability|. The sought probability is estimated using
  // the histogram as the reverse cumulant PDF, i.e., the sum of elements from
  // the end up until |index|. Now, since the sum of all elements is 1
  // (in Q30) by definition, and since the solution is often a low value for
  // |iat_index|, it is more efficient to start with |sum| = 1 and subtract
  // elements from the start of the histogram.
  int inverse_probability = (1 << 30) - probability;
  size_t index = 0;        // Start from the beginning of |buckets_|.
  int sum = 1 << 30;       // Assign to 1 in Q30.
  sum -= buckets_[index];
  
  while ((sum > inverse_probability) && (index < buckets_.size() - 1)) {
    // Subtract the probabilities one by one until the sum is no longer greater
    // than |inverse_probability|.
    ++index;
    sum -= buckets_[index];
  }

  return static_cast<int>(index);
}

​

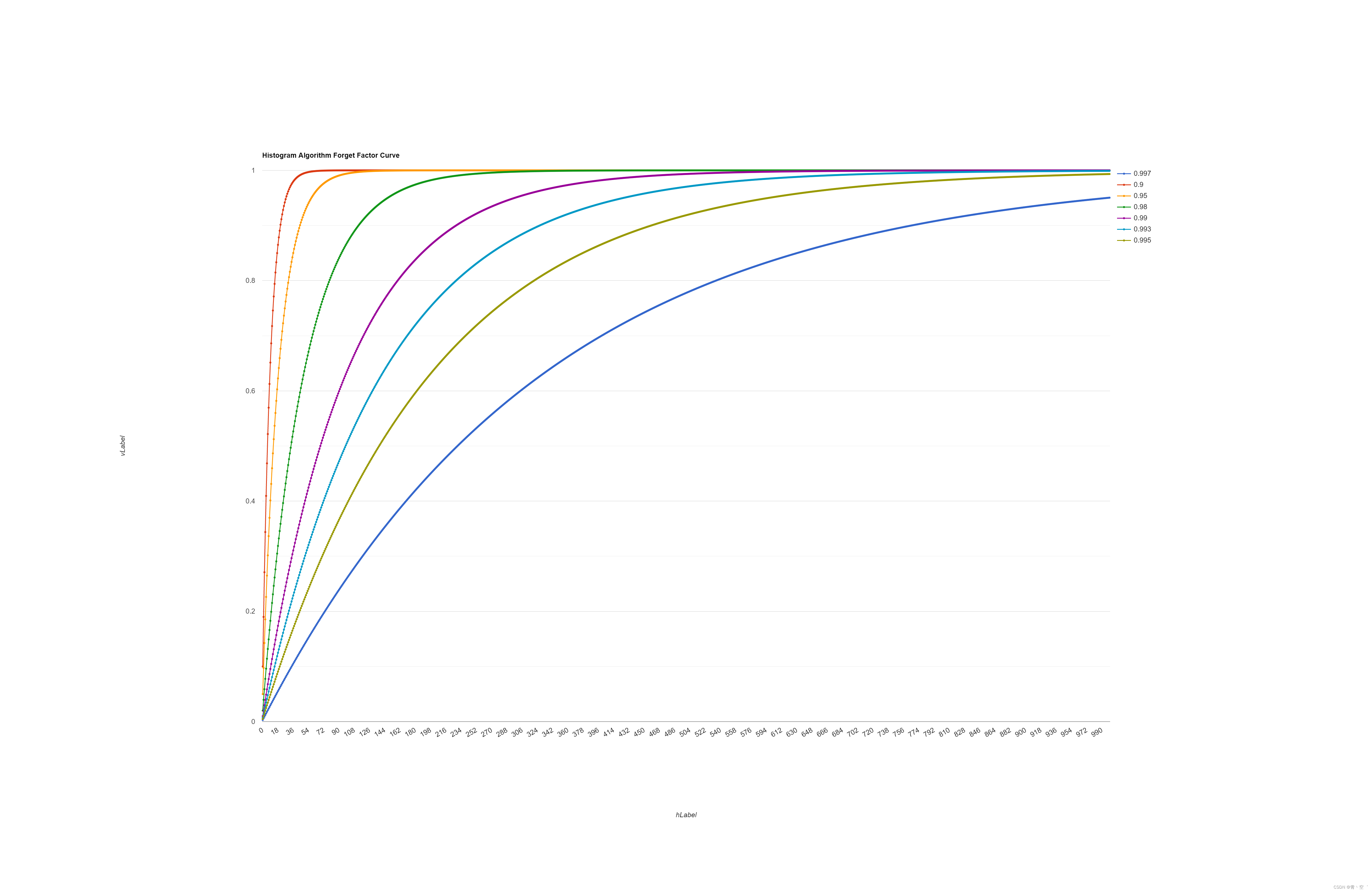
遗忘因子曲线

测试曲线,调整遗忘因子提高抖动估计灵敏度:

#include <iostream>
#include <cstdint>
#include <vector>

uint32_t packet_loss_rate_ = 0;

int main()
{
  std::vector<int> input;
  std::vector<float> buckets;
  float forget_factor = 0.9993;
  float val = 0;

  for (size_t k = 0; k < 1000; k ++) {
    val = val * forget_factor + (1-forget_factor);
    buckets.push_back(val);
  }

  for (int i = 0; i < 1000; ++i) {
    std::cout << buckets[i]<< " ";
  }

  return 0;
}