上一章——认识神经网络
新课P54介绍了强人工智能概念，P55到P58解读了矩阵乘法在代码中的应用，P59，P60介绍了在Tensflow中实现神经网络的代码及细节，详细的内容可以自行观看2022吴恩达机器学习Deeplearning.ai课程，专栏中就不再赘述。
文章目录
- 激活函数的替代方案
- Sigmoid函数
- ReLU函数
- 线性函数
- 激活函数的选择
- Output层
- 隐藏层
- 为什么模型需要激活函数
激活函数的替代方案
Sigmoid函数
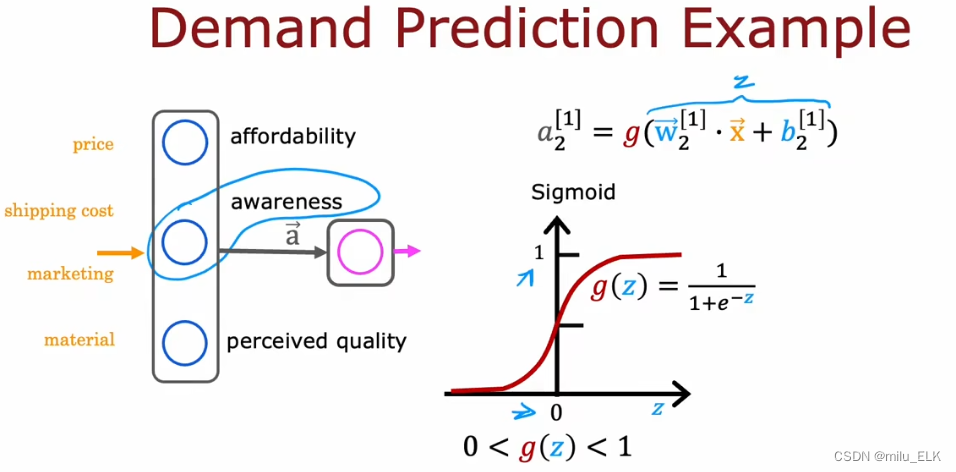
在逻辑回归中，我们使用的激活函数是Sigmoid函数，又称逻辑函数，它能预测(0,1)区间内的值，因此我们常常会在二分问题中使用。
ReLU函数
如果我们想要取到更大的正值，我们可以使用这个激活函数来代替，如图右边所示。
这个函数称为ReLU函数（Rectified Linear Unit），即修正线性单元，
R
e
L
U
:
g
(
z
)
=
m
a
x
(
0
,
z
)
ReLU:g(z)=max(0,z)
ReLU:g(z)=max(0,z)
其中当
z
<
0
z<0
z<0时，
g
(
z
)
=
0
g(z)=0
g(z)=0,
z
>
0
z>0
z>0时,
g
(
z
)
=
z
g(z)=z
g(z)=z
在实际工作中，ReLU函数的使用会更加广泛一些，
线性函数
线性激活函数
g
(
z
)
=
z
g(z)=z
g(z)=z,我们也可以称它没有使用任何激活函数，因为输入量为z，输出激活量
a
=
g
(
z
)
=
z
a=g(z)=z
a=g(z)=z,实际上没有任何变化。
激活函数的选择
激活函数如何选择取决于你需要一个什么样的输出量，我们以上面提到的几种激活函数为例
Output层
如果你要选择输出层的激活函数，那么最后得到的就是想要预测的结果，假如你想要预测的结果是一个二分问题，那么其预测值应当是处于0，1之间的，我们会选择逻辑函数；
假如你是要预测股票的涨跌，那么股票的跌可以视为负数，涨视为正数，因此你的输出层激活函数需要有正有负，我们就会选择线性激活函数，使得它有负值。
假设你要预测房价，那么房价一定不会是负数，我们不接受负值的出现，因此你可以选择ReLU函数来进行预测。
以上只是举我们讲过的几种激活函数为例，总而言之需要根据实际要求来选择激活函数，
以上仅是针对输出层，并不对隐藏层适用。
隐藏层
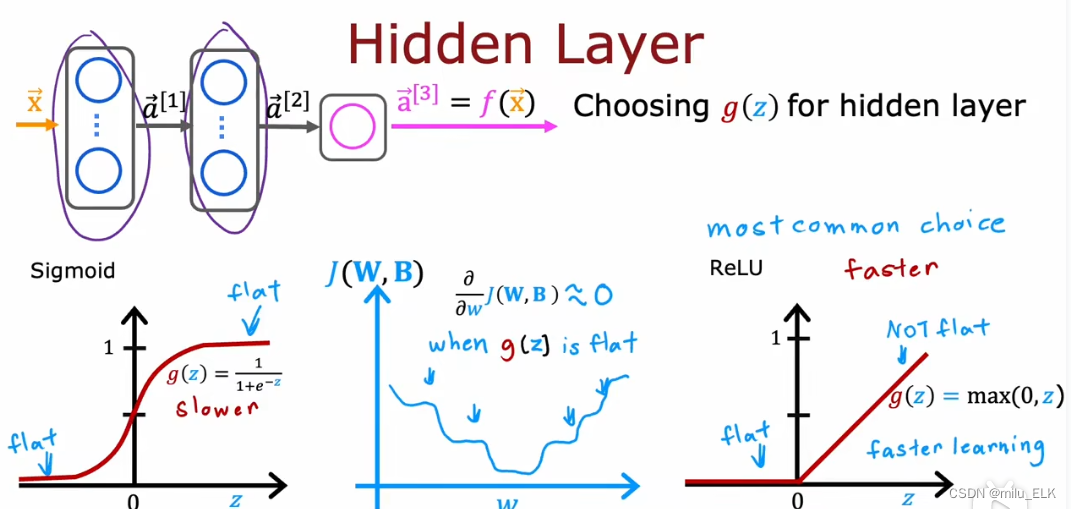在上一节介绍神经网络的时候，隐藏层使用的是Sigmoid函数，然而实际上ReLU或者其他函数更好，
- ReLU函数的计算比Sigmoid更简单，更快速
- ReLU函数的梯度下降速度比Sigmoid更快
如果仔细观察Sigmoid函数的代价函数（上图蓝色部分函数），会发现Sigmoid的函数形状并不是很适合梯度下降，并且随着Z的增大或缩小，Sigmoid函数的图像会趋于平坦，这就导致了 d J d w ≈ 0 \frac{dJ}{dw}≈0 dwdJ≈0,从而导致了梯度下降速度会越来越慢，而ReLU函数不会有这样的问题。一般来说，大部分情况下在隐藏层用ReLU函数都会更好。
为什么模型需要激活函数
我们的模型能不能不使用任何激活函数（仅线性激活函数）？答案是否定的，首先，从建立神经网络的目的来看，设置激活函数的目的就是为了向神经元添加非线性的输入来实现更复杂的计算，如果不使用激活函数，那么也没必要使用神经网络。
如果神经网络不使用激活函数，会发生什么情况？如下图所示
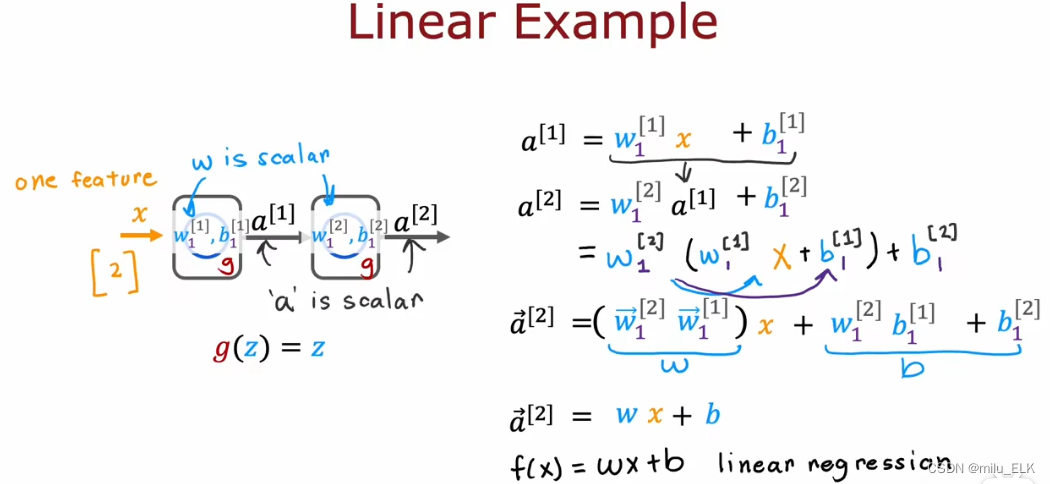
假设我们的神经网络的隐藏层和输出层使用的全部都是线性激活函数，那么
a
[
1
]
=
w
1
[
1
]
x
+
b
1
[
1
]
a^{[1]}=w^{[1]}_1x +b^{[1]}_1
a[1]=w1[1]x+b1[1],
a
[
2
]
=
w
1
[
2
]
a
[
1
]
+
b
1
[
2
]
a^{[2]}=w^{[2]}_1a^{[1]} +b^{[2]}_1
a[2]=w1[2]a[1]+b1[2]
我们将
a
[
2
]
a^{[2]}
a[2]式子中的
a
[
1
]
a^{[1]}
a[1]替换，就能得到
a
[
2
]
=
w
1
[
2
]
(
w
1
[
1
]
x
+
b
1
[
1
]
)
+
b
1
[
2
]
a^{[2]}=w^{[2]}_1(w^{[1]}_1x +b^{[1]}_1) +b^{[2]}_1
a[2]=w1[2](w1[1]x+b1[1])+b1[2]
展开后得到
a
[
2
]
=
(
w
1
[
2
]
w
1
[
1
]
)
x
+
w
1
[
2
]
b
1
[
1
]
+
b
1
[
2
]
a^{[2]}=(w^{[2]}_1w^{[1]}_1)x +w^{[2]}_1b^{[1]}_1 +b^{[2]}_1
a[2]=(w1[2]w1[1])x+w1[2]b1[1]+b1[2],将
(
w
1
[
2
]
w
1
[
1
]
)
设为
w
，
(
w
1
[
2
]
b
1
[
1
]
+
b
1
[
2
]
)
设为
b
就得到了
a
[
2
]
=
w
x
+
b
(w^{[2]}_1w^{[1]}_1)设为w，(w^{[2]}_1b^{[1]}_1 +b^{[2]}_1)设为b就得到了 a^{[2]}=wx +b
(w1[2]w1[1])设为w，(w1[2]b1[1]+b1[2])设为b就得到了a[2]=wx+b
也就是说，经过了两层的线性函数的计算，实际上也就相当于进行一次线性函数计算，那么n层线性激活函数的神经网络实际只相当于进行一次线性函数计算。也就是说如果不采用任何激活函数，整个神经网络和线性函数没有差别。所以，如果不使用激活函数，神经网络并不能提升进行复杂计算的能力，整个模型相当于逻辑回归。
在未来的学习中，我们也会接触到其他的激活函数，理解激活函数的作用，选择适宜的激活函数，将对我们神经网络的搭建具有重大意义。
下一章——多分类问题
