已知方阵A的不变因子：

1. 求谱半径
2. 求矩阵级数
3. 判断矩阵幂级数的收敛性
   
   若矩阵B的某个算子范数小于1，则I-B可逆。
   
   
   

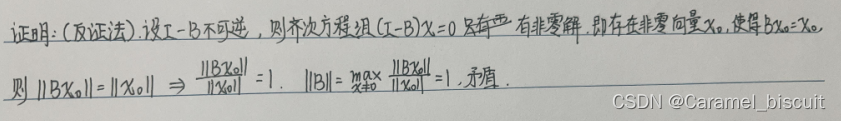
矩阵分析

任何相容矩阵范数都存在与之相容的向量范数。

盖尔圆盘定理一的证明

椭圆范数的证明
若||.||是C^m上的向量范数，A为列满秩矩阵，则||A.||是Cⁿ上的向量范数。

椭圆范数的应用

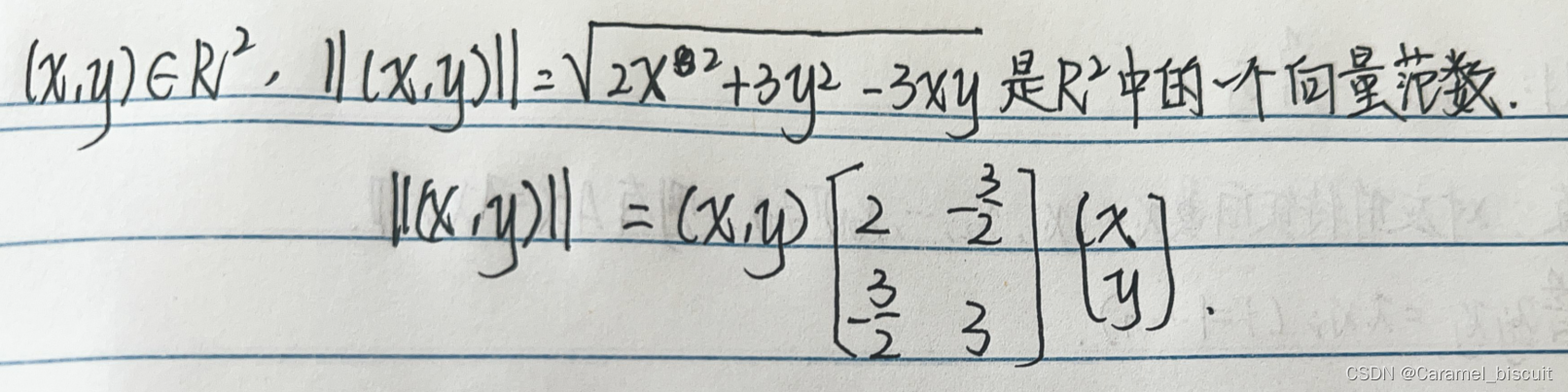
Rayleigh商

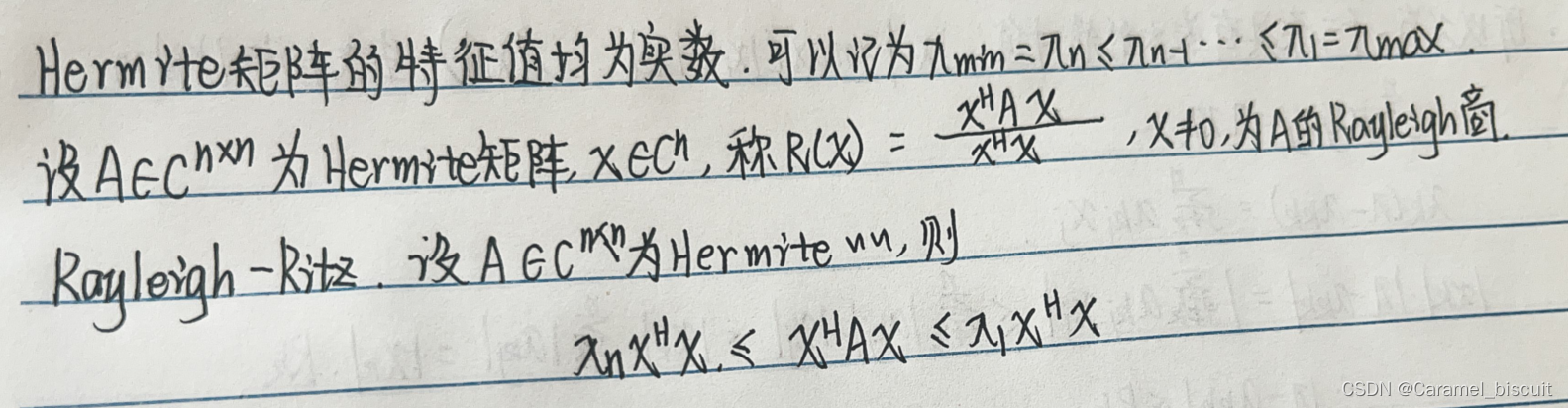
R(A⁺)=R(A^H)

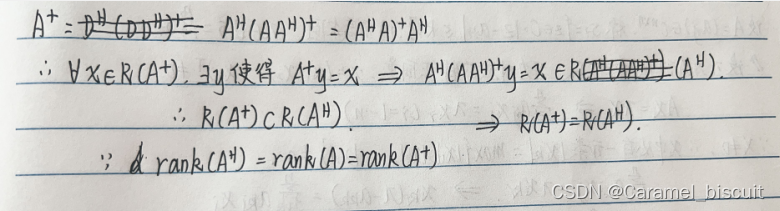
A⁺=A^H(AA^H)⁺=(A^HA)⁺A^H

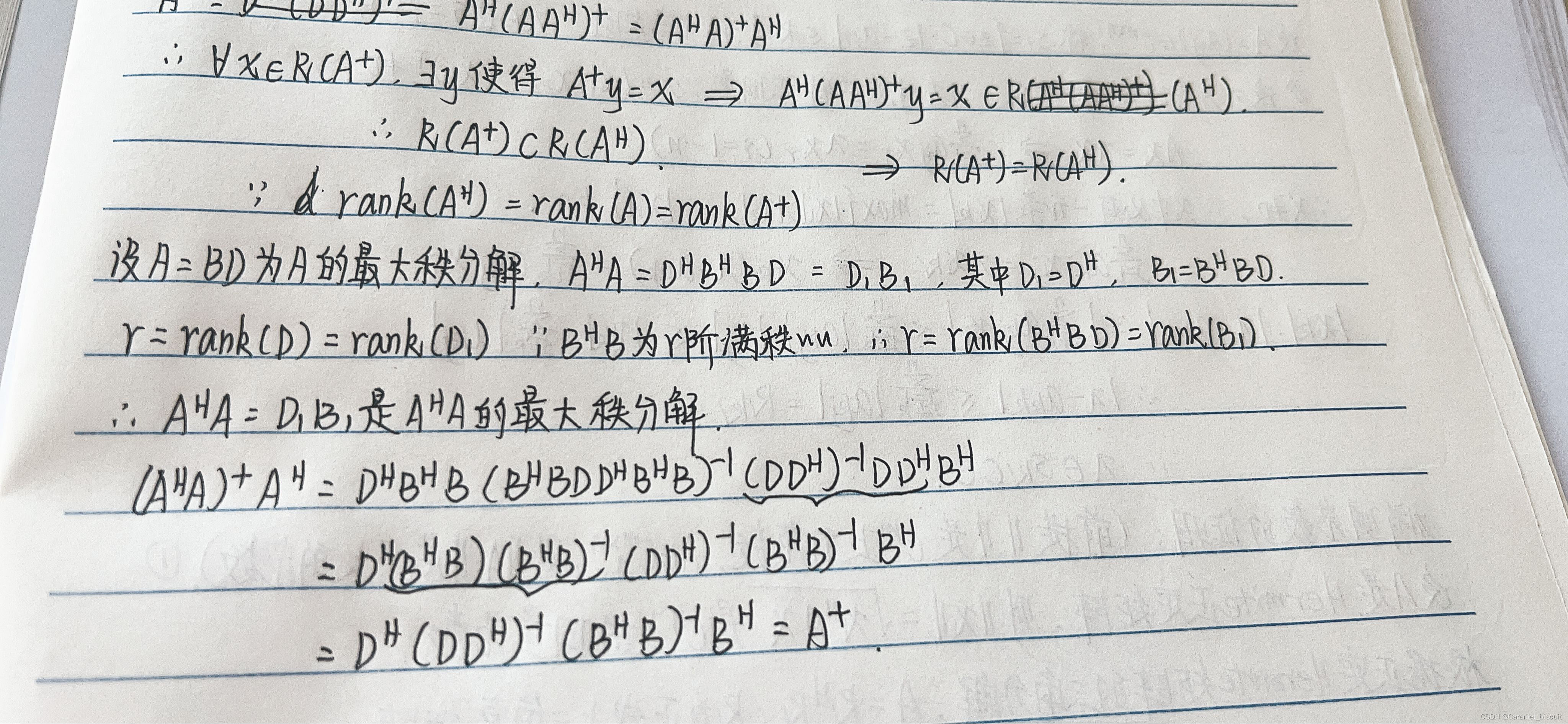
当A的某算子范数小于1时，证明E-A可逆

证明自反广义逆

1. AGA=A
2. rank(G)=rank(A)

证明G=YZ是A的自反广义逆

B=[A⁺ A⁺]

设T是线性空间V上的投影，则投影的值域和核互为直和补。

维数定理

直和

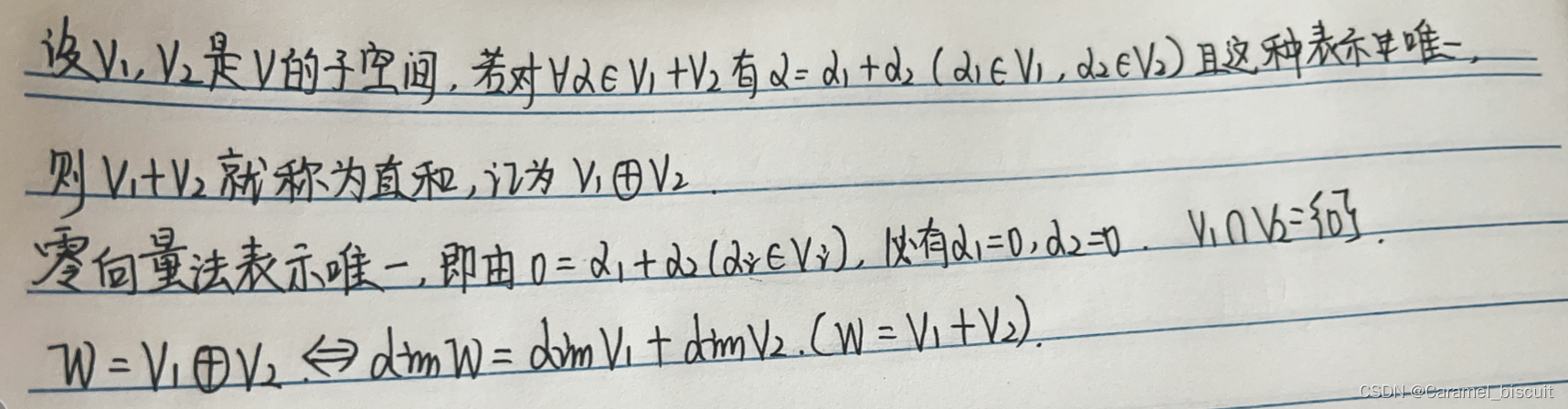
正规矩阵A的特征值的模等于A的奇异值

rank(A)=rank(A^H)=rank((A^HA)=rank((AA^H)

三角矩阵的结论

1. 上三角矩阵的逆仍是上三角矩阵，且对角元是R对角元的倒数。
2. 两个上三角矩阵的乘积仍是上三角矩阵，且对角元是R1,R2对角元的乘积。
3. 酉矩阵的逆还是酉矩阵，酉矩阵的乘积仍是酉矩阵。