D3-双指针算法-归并两个有序数组&&Two Sum
- 什么是双指针算法
- 力扣88. 合并两个有序数组
- 思路
- 代码
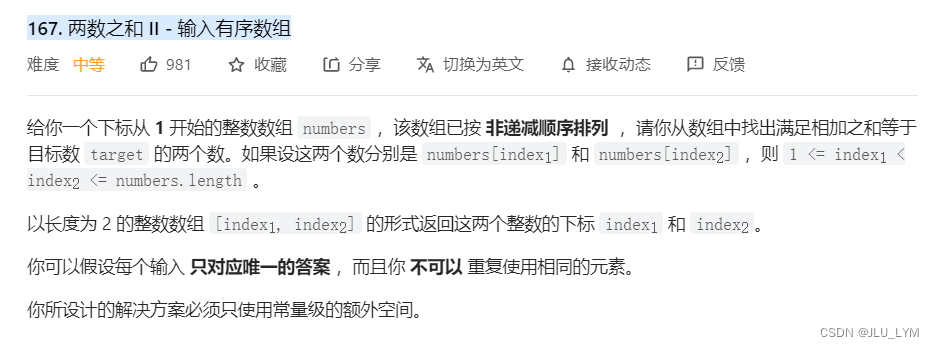
- 力扣167. 两数之和 II - 输入有序数组
- 思路
- 思路一:时间复杂度O(nlogn)算法
- 代码
- 思路二:时间复杂度O(n)--双指针算法
- 代码
什么是双指针算法
1、双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。也可以延伸到多
个数组的多个指针。
2、若两个指针指向同一数组,遍历方向相同且不会相交,则也称为滑动窗口(两个指针包围的区域即为当前的窗口),经常用于区间搜索。
3、若两个指针指向同一数组,但是遍历方向相反,则可以用来进行搜索,待搜索的数组往往是排好序的。
4、常见的c++指针操作方式:
int x;
int * p1 = &x; // 指针可以被修改,值也可以被修改
const int * p2 = &x; // 指针可以被修改,值不可以被修改(const int)
int * const p3 = &x; // 指针不可以被修改(* const),值可以被修改
const int * const p4 = &x; // 指针不可以被修改,值也不可以被修改
// addition是指针函数,一个返回类型是指针的函数
int* addition(int a, int b) {
int* sum = new int(a + b);
return sum;
}
int subtraction(int a, int b) {
return a - b;
}
int operation(int x, int y, int (*func)(int, int)) {
return (*func)(x,y);
}
// minus是函数指针,指向函数的指针
int (*minus)(int, int) = subtraction;
int* m = addition(1, 2);
int n = operation(3, *m, minus);
力扣88. 合并两个有序数组
题目链接:88. 合并两个有序数组


思路
1、这种题是最基本的套路提,最简单的想法就是:两个指针在两个数组头部进行遍历,每次从两个指针指向的位置处选择小的元素,最后在把没放进去的放进去即可。
2、但需要额外存于一个新数组,空间复杂度不好。
3、所以,采取优化手段,我们两个指针,从两个数组尾部开始遍历,每次选大的加入nums尾部(已经提前开好空间了),这样就可以省下空间
代码
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m - 1, j = n - 1, k = m + n - 1;//分别指向nums1,nums2,k用于在nums1尾部写入新数据
while (i >= 0 && j >= 0) {
if (nums2[j] > nums1[i]) {//每次放入大的元素进入nums1尾部
nums1[k] = nums2[j];
j--;
}
else {
nums1[k] = nums1[i];
i--;
}
k--;
}
while (i >= 0) {//把剩余的放进去
nums1[k] = nums1[i];
i--;
k--;
}
while (j >= 0) {
nums1[k] = nums2[j];
j--;
k--;
}
}
};
力扣167. 两数之和 II - 输入有序数组
题目链接:167. 两数之和 II - 输入有序数组

思路
拿来这个题,最基本的想法就是,我遍历一遍数组,访问到i处时,再遍历一遍数组,查找target-numbers[i]是否在数组中,这是O(n^2)的想法,也是最朴素的想法。
思路一:时间复杂度O(nlogn)算法
1、但是,只要是涉及在有序数组中查找一个数值的问题的时候,一定一定一定不要犹豫!直接选择二分查找!
2、注意读题,答案中下标顺序,一定是递增的,所以从左到右枚举第一个i,再对第二个数二分查找就行,返回下标
3、注意,第二个数的下标,一定不能和第一个数的下标重合,二分查找的时候注意判断。
4、根据题意,最后下标都加一
代码
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {//二分查找
int n = numbers.size();
for (int i = 0; i < n; i++) {
int one = numbers[i];
int two = target - one;
int pos = find(numbers, 0, n - 1, two, i);
if (pos != -1) {
return { i + 1,pos + 1 };
}
}
return {};
}
//二分查找参数说明:数组(传入引用,加快效率),左边界,右边界,目标数,第一个数对应的下标
int find(vector<int>& numbers, int left, int right, int two, int i) {//二分查找
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
if (numbers[mid] == two && mid != i) {
return mid;
}
else if (numbers[mid] > two) {
return find(numbers, left, mid - 1, two, i);
}
return find(numbers, mid + 1, right, two, i);
}
};
思路二:时间复杂度O(n)–双指针算法
1、我们一定要善于具体化搜索过程,根据朴素搜索定义,相当于一个指针i在一个轴上面搜索,另一个指针j在一个轴上面搜索,也就是,可以具体看做在一个二维平面上搜索,每一个(i,j)里面的值,代表着numbers[i]+numbers[j],相当于在一个二维矩阵(已经排好序)中搜索目标值。
2、但是,由于题意,我们只能在上半三角矩阵中搜索,如图中白色框框:
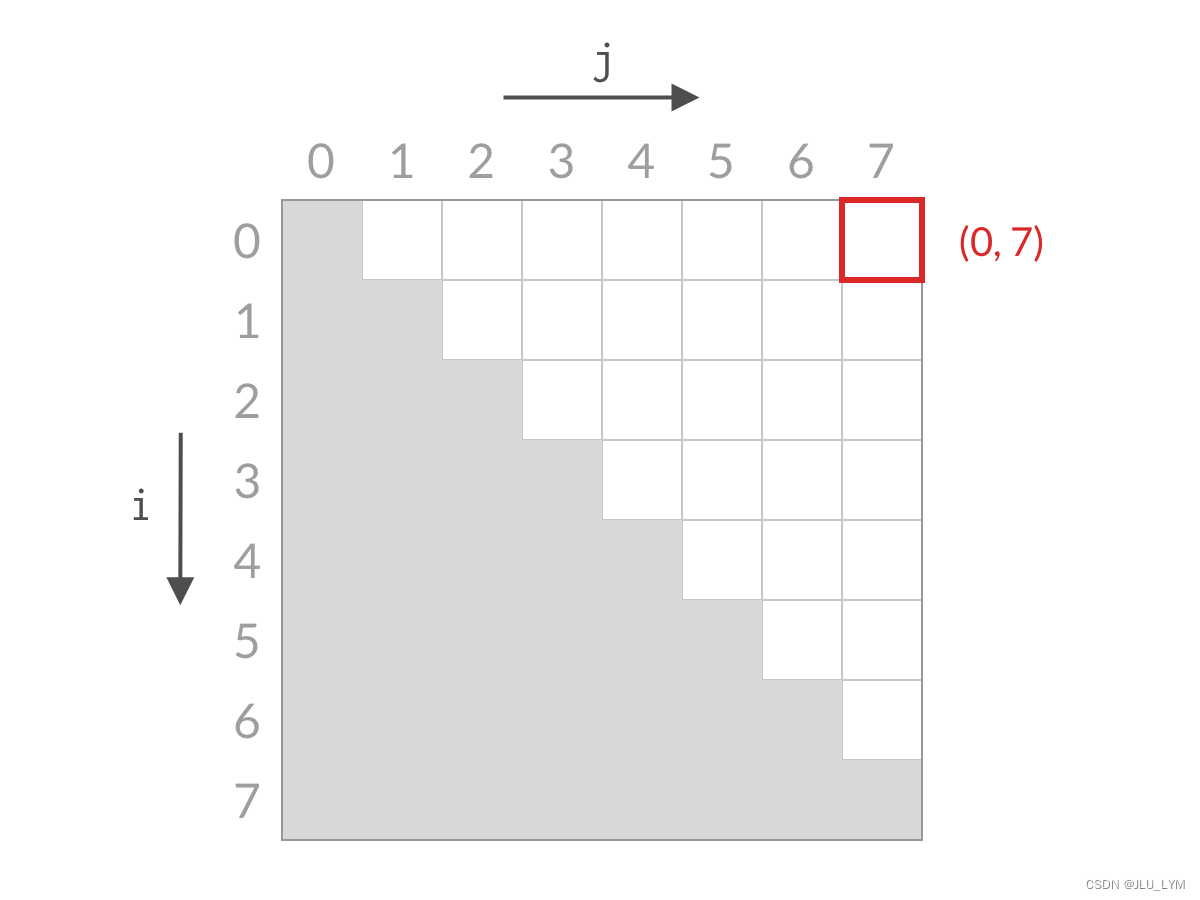
3、所以,这道题就转化为了,和240. 搜索二维矩阵 II一模一样的思路,从左下角或者右上角开始,在O(n)内即可完成搜索。下面,我将介绍这种搜索的原理
4、因为本体限制,所以只能从右上角在(0,7)处开始搜索,如果不是目标要么大于target,要么小于target
当小于target时,因为在0行中,(0,7)已经是最大了,再想要更大的数,i=0根本满足不了,直接省略0行,i++
当大于target时,因为在7列中,(0,7)已经是最小了,再想要更小的数,j=7根本满足不了,直接省略7列,j - -
5、综上,可以看到,无论 结果是大了还是小了,我们都可以排除掉一行或者一列的搜索空间。经过 n 步以后,就能排除所有的搜索空间,检查完所有的可能性。搜索空间的减小过程如下面动图所示:
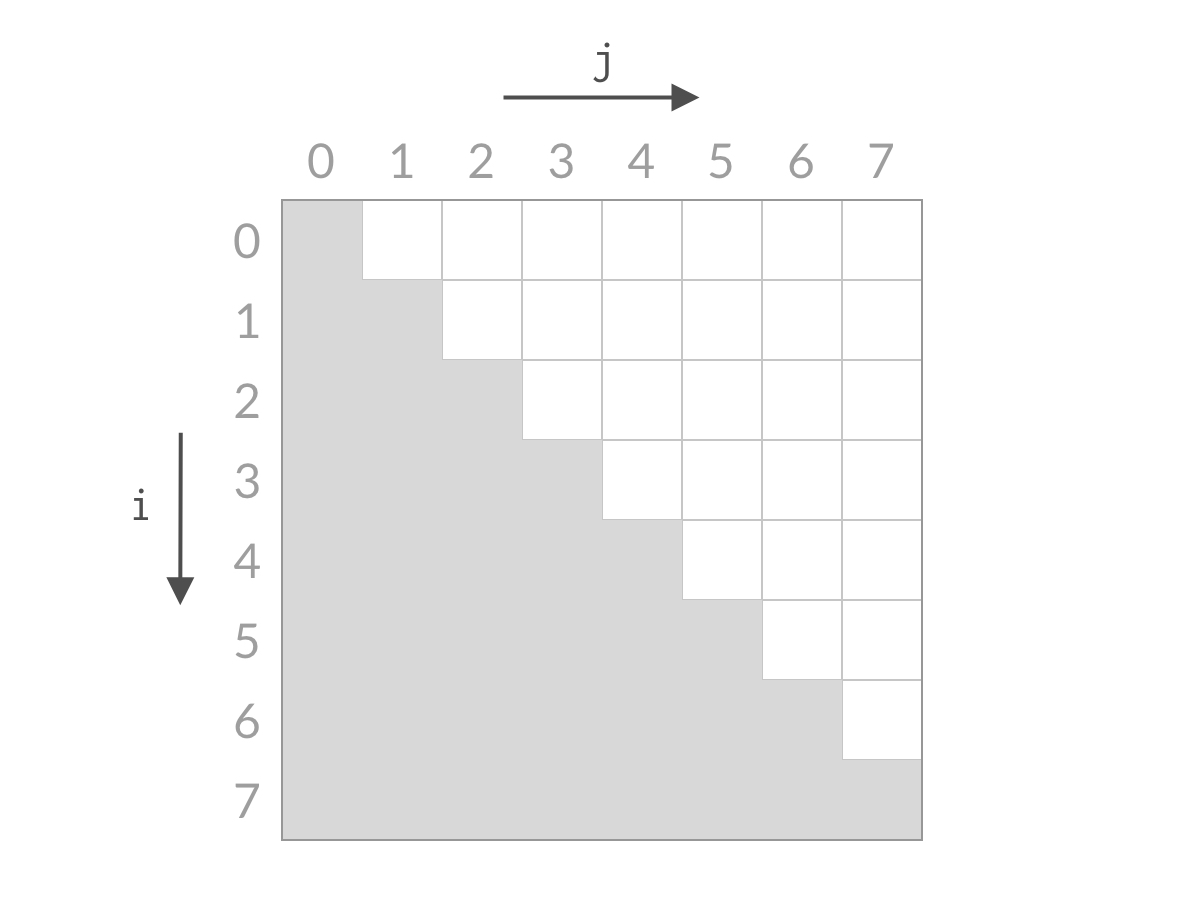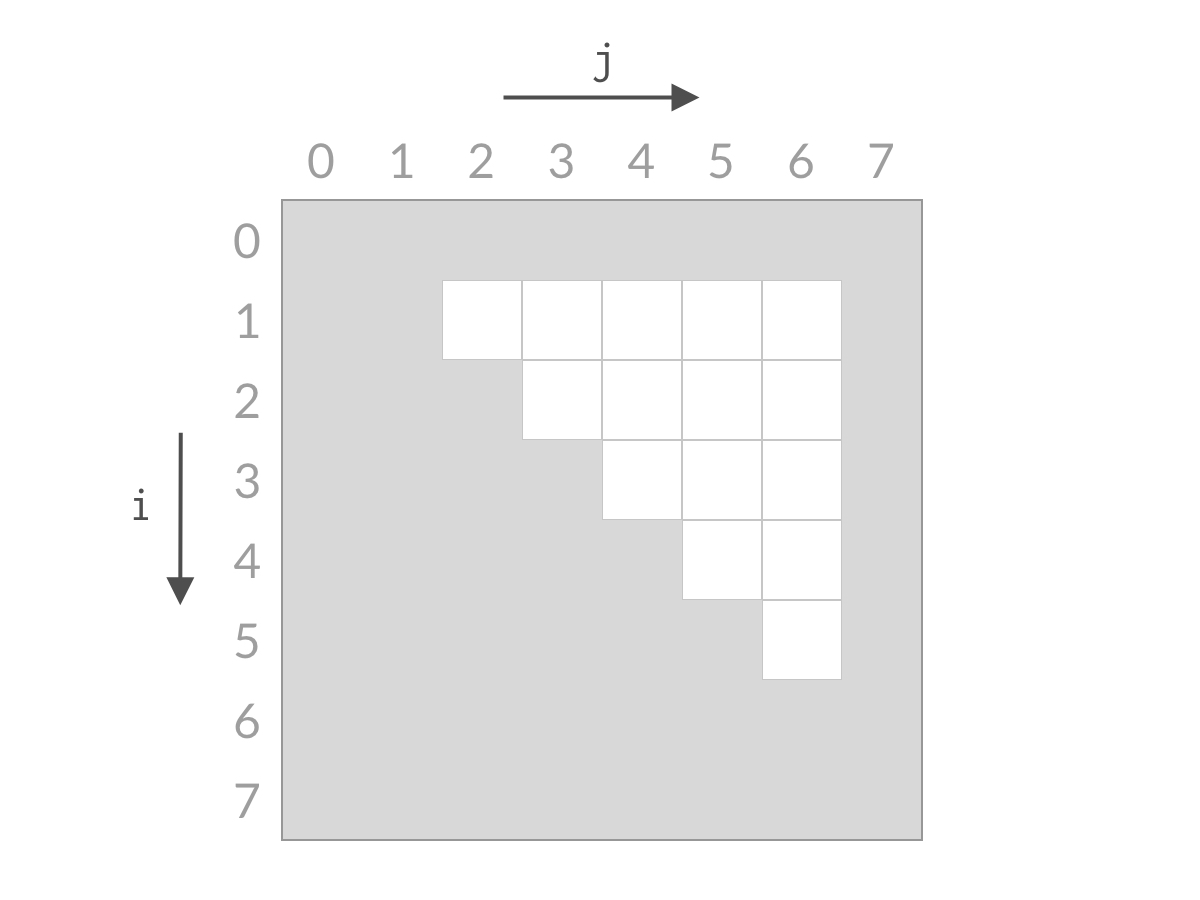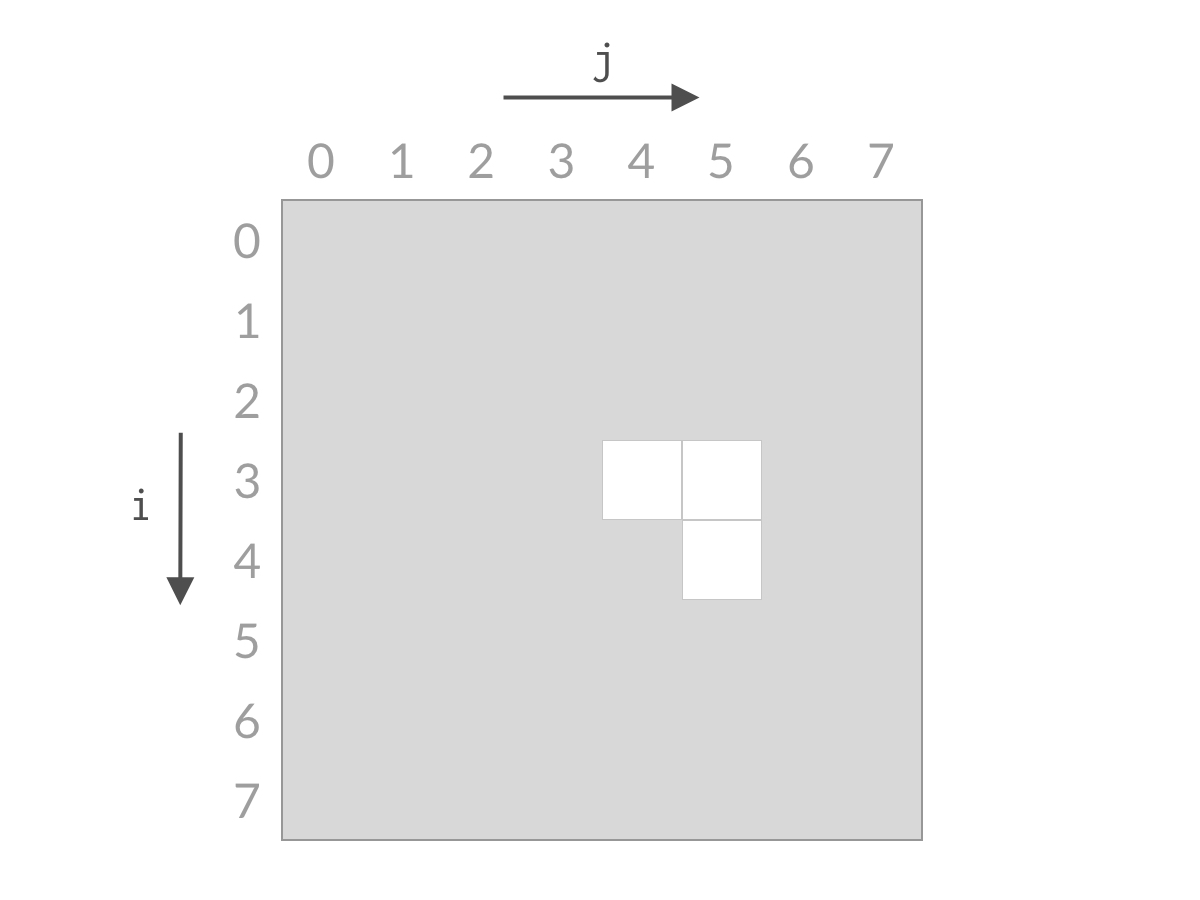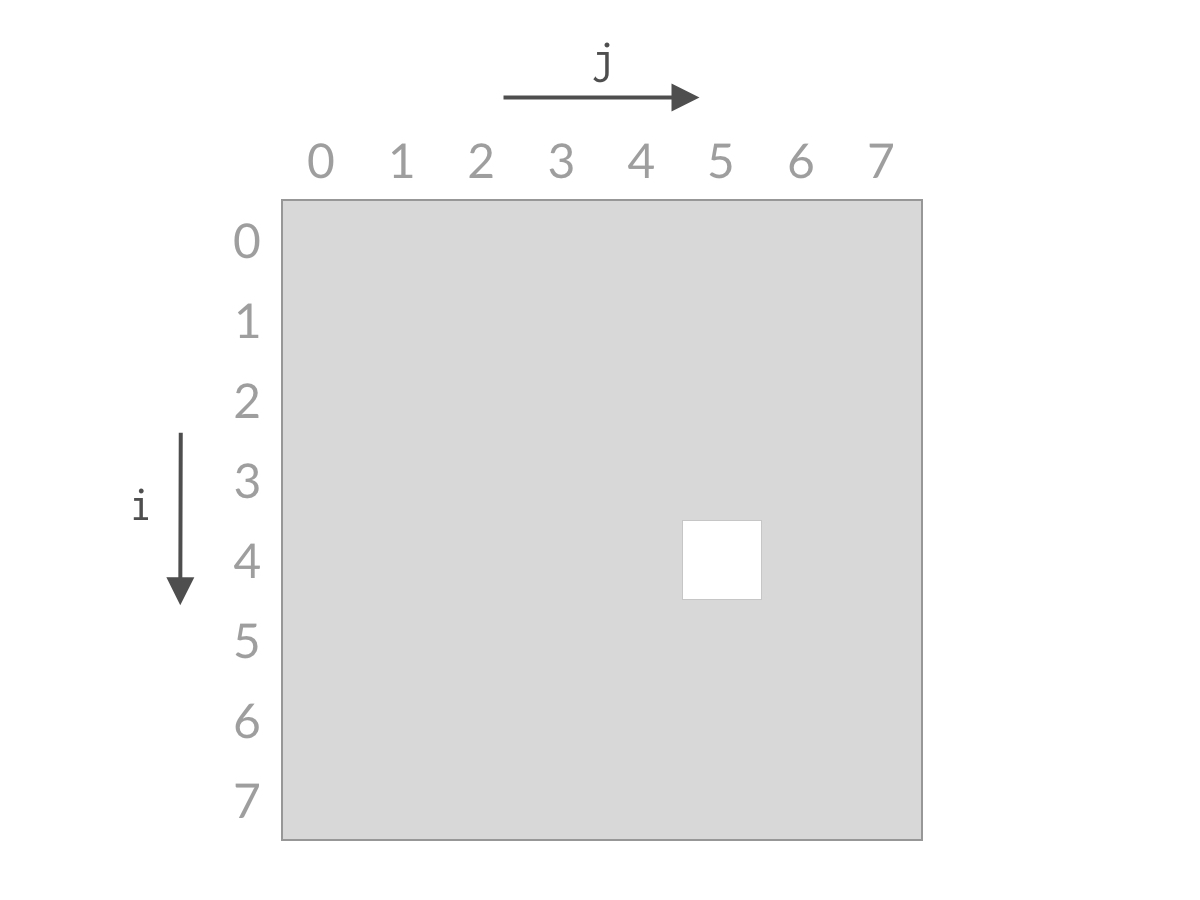
这也就是,这一类已经全部排序完毕的二维空间中,快速查找的思路。
代码
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {//双指针
int i = 0, j = numbers.size() - 1;
while (i < j) {
if (numbers[i] + numbers[j] < target) {
i++;
}
else if (numbers[i] + numbers[j] > target) {
j--;
}
else {
return { i+1,j+1 };
}
}
return {};
}
};