( A, B )---2*30*2---( 1, 0 )( 0, 1 )
做一个网络让输入只有2个节点,每个训练集里有两张图片,让B的训练集全为0,排列组合A,观察迭代次数平均值的变化。
共得到32组数据,
| 差值结构 | A-B | 迭代次数 | ||
| 1 | 1 | 3*2*0*0 | 10400.236 | |
| 1 | 0 | 3*2*0*0 | 10400.236 | |
|
| ||||
| 1 | 1 | 3*1*0*0 | 10480.94 | |
| 0 | 1 | 3*1*0*0 | 10480.94 | |
|
| ||||
| 1 | 0 | 2*3*0*0 | 10510.819 | |
| 1 | 1 | 2*3*0*0 | 10510.819 | |
|
| ||||
| 0 | 1 | 1*3*0*0 | 10526.457 | |
| 1 | 1 | 1*3*0*0 | 10526.457 | |
| 1 | 1 |
| 3*3*0*0 | 22701.04 |
| 1 | 1 |
| 3*3*0*0 | 22701.04 |
| 0 | 1 | 1*1*0*0 | 27276.94 | |
| 0 | 1 | 1*1*0*0 | 27276.94 | |
|
| ||||
| 1 | 0 | 2*2*0*0 | 27280.497 | |
| 1 | 0 | 2*2*0*0 | 27280.497 | |
| 1 | 1 | 3*0*0*0 | 32918.668 | |
| 0 | 0 | 3*0*0*0 | 32918.668 | |
|
| ||||
| 0 | 0 | 0*3*0*0 | 33044.91 | |
| 1 | 1 | 0*3*0*0 | 33044.91 | |
| 0 | 1 | 1*2*0*0 | 33711.02 | |
| 1 | 0 | 1*2*0*0 | 33711.02 | |
|
| ||||
| 1 | 0 | 2*1*0*0 | 33778.045 | |
| 0 | 1 | 2*1*0*0 | 33778.045 | |
| 0 | 0 | 0*2*0*0 | 40957.01 | |
| 1 | 0 | 0*2*0*0 | 40957.01 | |
|
| ||||
| 0 | 1 | 1*0*0*0 | 41001.884 | |
| 0 | 0 | 1*0*0*0 | 41001.884 | |
|
| ||||
| 0 | 0 | 0*1*0*0 | 41127.121 | |
| 0 | 1 | 0*1*0*0 | 41127.121 | |
|
| ||||
| 1 | 0 | 2*0*0*0 | 41284.698 | |
| 0 | 0 | 2*0*0*0 | 41284.698 | |
| 0 | 0 | 0*0*0*0 | ∞ | |
| 0 | 0 | 0*0*0*0 | ∞ | |
不考虑A全为0迭代次数为无穷大的最后一组,迭代次数不同的网络只有6种,
| 差值结构 | A-B | 迭代次数 | ||
| 1 | 1 | 3*2*0*0 | 10400 | |
| 1 | 0 | 3*2*0*0 | 10400 | |
| 1 | 1 |
| 3*3*0*0 | 22701 |
| 1 | 1 |
| 3*3*0*0 | 22701 |
| 0 | 1 | 1*1*0*0 | 27277 | |
| 0 | 1 | 1*1*0*0 | 27277 | |
| 1 | 1 | 3*0*0*0 | 32919 | |
| 0 | 0 | 3*0*0*0 | 32919 | |
| 0 | 1 | 1*2*0*0 | 33711 | |
| 1 | 0 | 1*2*0*0 | 33711 | |
| 0 | 0 | 0*2*0*0 | 40957 | |
| 1 | 0 | 0*2*0*0 | 40957 | |
这次继续用质心的方法去排序这6组迭代次数,所不同的是,假设训练集A中的4个点表示的是球体赤道面内接正方形的4条边。
| 0 | 0 | 0*2*0*0 | 40957 | |
| 1 | 0 | 0*2*0*0 | 40957 |
对第一组情况,就意味这这个正方形只有1条边有质量,其他三条边的质量为0,显然在重力的作用下,这个形态将很快趋于稳定,这条有质量的边将处于最低点。而此时这个形态的质心与这个形态最低点所在平面是重合的,质心为0.
| 0 | 1 | 1*2*0*0 | 33711 | |
| 1 | 0 | 1*2*0*0 | 33711 |
第二种情况,用两条对边去表达,
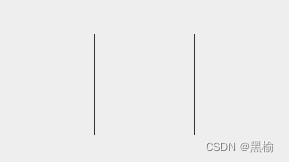
一种稳定情况是两条边都竖起来,假设边长为50,此时质心为25.另一种情况是两条边在重力的作用下处于水平面,此时质心为0。如果两种情况各占一半平均质心为12.5.
| 1 | 1 | 3*0*0*0 | 32919 | |
| 0 | 0 | 3*0*0*0 | 32919 |
第3中情况,用两条相邻的边去表达
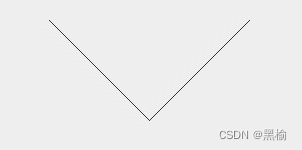
在这种情况下只有一种稳定态,两条边都在垂直平面内,此时质心为17.675.
| 1 | 1 |
| 3*3*0*0 | 22701 |
| 1 | 1 |
| 3*3*0*0 | 22701 |
第4种情况

如果4条边质量相同,则应该处于水平,质心为0.
| 1 | 1 | 3*2*0*0 | 10400 | |
| 1 | 0 | 3*2*0*0 | 10400 |
第5中情况
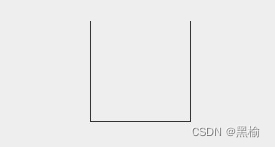
这3条边应该是垂直的,且只有一种稳定态,质心高为16.7.
则得到表格
| 差值结构 | A-B | 迭代次数 | 质心h | |||
| 1 | 1 | 3*2*0*0 | 10400 | 16.7 | ||
| 1 | 0 | 3*2*0*0 | 10400 | |||
| 1 | 1 |
| 3*3*0*0 | 22701 | 0 | |
| 1 | 1 |
| 3*3*0*0 | 22701 | ||
| 0 | 1 | 1*1*0*0 | 27277 | |||
| 0 | 1 | 1*1*0*0 | 27277 | |||
| 1 | 1 | 3*0*0*0 | 32919 | 17.675 | ||
| 0 | 0 | 3*0*0*0 | 32919 | |||
| 0 | 1 | 1*2*0*0 | 33711 | 12.5 | ||
| 1 | 0 | 1*2*0*0 | 33711 | |||
| 0 | 0 | 0*2*0*0 | 40957 | 0 | ||
| 1 | 0 | 0*2*0*0 | 40957 | |||
只要假设对称部分和非对称部分是被3*3*0*0天然分开的,就可以解释为什么3*2*0*0的质心比3*0*0*0还要小,迭代次数反比3*0*0*0要大的现象。也可以解释为什么3*3*0*0和0*2*0*0的质心都是0,3*3*0*0的迭代次数要小的多,因为3*3*0*0就是对称与非对称的分界线。
而且前面已有大量的实验表明,神经网络是可以区分左右和上下的,所以可以理解为神经网络表达的这种引力是宇称不守恒的,
| 0 | 1 | 1*1*0*0 | 27277 | |
| 0 | 1 | 1*1*0*0 | 27277 | |
| 1 | 1 | 3*0*0*0 | 32919 | |
| 0 | 0 | 3*0*0*0 | 32919 |
对于一个正方形,横边和竖边是没有区别的,但在一个宇称不守恒的引力环境中,横竖两条边相对45度线就是左右的差别,因此在质心相同的情况下迭代次数可能就会有区别。
所以这个内嵌球的假设相当于认为,迭代次数与质心成反比,但形态有对称和非对称的天然差别,且这个引力场宇称不守恒。