定义

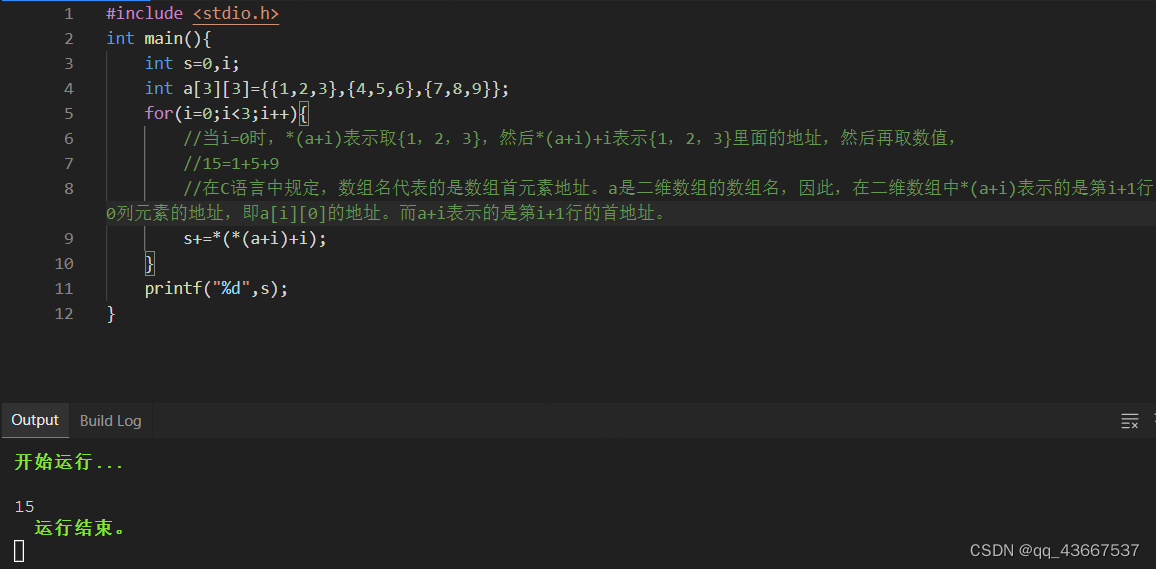
每相邻两个节点升高一层，增加一个指针，让指针指向下下个节点；上面每一层链表的节点个数，是下面一层的节点个数的一半，这样在查找的时候就类似于二分查找。

优化

如上图所示，插入或删除的时候会破坏跳表中这种2：1的对应关系
解决方法：不再要求严格的比例关系，把结点插入到相应位置之后，再给其随机出一个层数，保证每个结点的插入和删除操作和其他结点没关系，都是独立的，不需要调整其他结点的关系；
一般跳表会设计一个最大层数maxLevel的限制和一个多增加一层的概率p；
当p=1/2时，每个节点所包含的平均指针数目为2；
当p=1/4时，每个节点所包含的平均指针数目为1.33。

实现基本框架

定义跳表结点

每个跳表结点内部包含值域和指针数组域；

template <class T>
struct SkiplistNode{
	T _data;
	vector<SkiplistNode*> _nextv;

	SkiplistNode(T data, int level)
		:_data(data),
		_nextv(level, nullptr){
	}
};

实现基础结构

template <class T>
class Skiplist{
public:
	typedef SkiplistNode<T> Node;
private:
	Node* _head;  //头结点
	size_t _maxlevel = 10;  //跳表的最大层数
	double _p = 0.25;  //多增加一层的概率
};

构造函数

跳表初始状态下，仅有头结点，其层数为1，值为-1；

Skiplist() {
	srand(time(0));  //随机数种子
	_head = new Node(-1, 1);  //初始时，头结点为1层
}

实现基本操作

查找操作

从头结点开始，按从上层到下层的数据进行查找
target大于当前层下一个不为空的结点，向右走
target小于当前层下一个结点或下一个结点为空，向下走

	bool search(int target) {
		size_t level = _head->_nextv.size()-1;  //level表示层数的下标
		Node* cur = _head;
		while (level >= 0){
			if (cur->_nextv[level] != nullptr && target > cur->_nextv[level]->_data){
				//target大于当前层下一个不为空的结点，向右走
				cur = cur->_nextv[level];
			}
			else if (cur->_nextv[level] == nullptr || target < cur->_nextv[level]->_data){
				//target小于当前层下一个结点或下一个结点为空，向下走
				level--;
			}
			else
				return true;
		}
		return false;
	}

插入数据

先找待插入数据的位置，并且保留待插入位置的每一层的前一个结点
前一个结点：若需要向下查找，则当前结点为待插入结点当前层的前一个结点

vector<Node*> findPrevV(int num){
		int level = _head->_nextv.size() - 1;
		Node* cur = _head;

		vector<Node*> prevV(level + 1, _head); //初始其每层前一个结点都为_head

		while (level >= 0){
			if (cur->_nextv[level] != nullptr && num > cur->_nextv[level]->_data){
				cur = cur->_nextv[level];
			}
			else if (cur->_nextv[level] == nullptr || num <= cur->_nextv[level]->_data){
				//向下走，当前结点为待插入结点当前层的前一个结点
				prevV[level] = cur;
				--level;
			}
		}
		return prevV;
	}

插入结点，并从下到上连接该结点到跳表中

void add(int num) {
		//1.记录待插入结点每一层的前一个结点
		vector<Node*> prevV = findPrevV(num);

		//2.插入结点
		int n = randomLevel();
		Node* newnode = new Node(num, n);
		//若待插入结点的层数大于头结点的层数，升高_head及prevV数组的层数
		if (n > _head->_nextv.size()){
			_head->_nextv.resize(n, nullptr);
			prevV.resize(n, _head);  //高出层数的前一个结点都为_head
		}
		//从下到上连接新结点的前后结点到跳表中
		for (size_t i = 0; i < n; i++){
			newnode->_nextv[i] = prevV[i]->_nextv[i];
			prevV[i]->_nextv[i] = newnode;
		}
	}

删除某结点

先找待删除结点的位置，并且保存待删除结点的每一层的前一个结点
若待删除结点的第0层的前一个结点的下一个结点为空或其值不为num，说明num结点不在跳表中
删除num结点，自底向上对各层进行连接

bool erase(int num) {
		//1.先找到待删除结点每一层的前一个结点
		vector<Node*> prevV = findPrevV(num);
		
		//若num结点的第0层的前一个结点的下一个结点为空或其值不为num
		//说明num结点不在跳表中
		if (prevV[0]->_nextv[0] == nullptr || prevV[0]->_nextv[0]->_data != num){
			return false;
		}
		//2.删除num结点
		else{
			Node* delnode = prevV[0]->_nextv[0];
			for (int i = 0; i < delnode->_nextv.size(); i++){
				prevV[i]->_nextv[i] = delnode->_nextv[i];
			}
			delete delnode;
			return true;
		}
	}

打印跳表

从上到下，按层访问结点

void print(){
		int level = _head->_nextv.size() - 1;
		for (int i = level; i >= 0; i--){
			Node* cur = _head->_nextv[i];
			while (cur){
				cout << cur->_data << " ";
				cur = cur->_nextv[i];
			}
			cout << endl;
		}
	}

跳表与平衡搜索树和哈希表的对比

skiplist相比平衡搜索树(AVL树和红黑树)的优势：
a、skiplist实现简单，容易控制；
b、skiplist的额外空间消耗更低：平衡树节点存储每个值有三叉链，平衡因子/颜色等消耗；skiplist中p=1/2时，每个节点所包含的平均指针数目为2；skiplist中p=1/4时，每个节点所包含的平均指针数目为1.33。
skiplist相比哈希表而言：
缺点：哈希表查找的平均时间复杂度是O(1)，比skiplist快
优点：a、遍历数据有序；
b、消耗略小一点，哈希表存在链接指针和表空间消耗；
c、哈希表扩容有性能损耗；
d、哈希表在极端场景下哈希冲突高，效率下降厉害，需要红黑树补足接力。