引言

本节将系统介绍重参数化技巧。

回顾

神经网络的执行过程

上一节比较了概率图模型与神经网络结构，介绍了它们的各自特点。神经网络(这里指前馈神经网络结构)本质上是一个 函数逼近器：

• 基于一个复杂函数$\mathcal{Y}=f(\mathcal{X})$，可通过神经网络进行学习，并对该函数进行近似描述。
  
• 根据具体任务以及输出信息$\mathcal{Y}$的性质，去构建对应策略(目标函数/损失函数)：
  例如线性回归($\text{Linear Regression}$)任务中，使用最小二乘估计对预测结果${\mathcal{W}}^T{x}^{(i)}$和真实标签$y^{(i)}$之间的关联关系进行描述：
  这里省略了偏置信息$b$,并且$(x^{(i)},y^{(i)})$是数据集合中的一个样本。
  $$\mathcal{L}(\mathcal{W})=\sum _{i=1}^N||{\mathcal{W}}^T{x}^{(i)}-y^{(i)}|{|}^2$$
• 在确定目标函数后，使用梯度下降($\text{Gradient Descent,GD}$)方法配合反向传播算法($\text{Backward Propagation,BP}$)对神经网络内部权重、偏置参数进行学习与更新。

变分推断——重参数化技巧

在变分推断——重参数化技巧中，我们同样介绍过重参数化技巧：

• 针对难求解的($\text{Intractable}$)关于隐变量$\mathcal{Z}$的后验概率分布$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$，通过变分推断($\text{Variational Inference,VI}$)的手段，人为定义一个概率分布$\mathcal{Q}(\mathcal{Z})$去近似$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$：
  需要注意的是，这里的$\mathcal{Q}(\mathcal{Z})$并非指的关于隐变量$\mathcal{Z}$‘边缘概率分布’,而是条件概率分布$\mathcal{Q}(\mathcal{Z}\mid \mathcal{X})$缩写而成。
  $$\begin{array}{rl}\log \mathcal{P}(\mathcal{X})& ={\int }_{\mathcal{Z}}\mathcal{Q}(\mathcal{Z})\cdot \left[\frac{\mathcal{P}(\mathcal{X},\mathcal{Z})}{\mathcal{Q}(\mathcal{Z})}\right]d\mathcal{Z}-{\int }_{\mathcal{Z}}\mathcal{Q}(\mathcal{Z})\cdot \left[\frac{\mathcal{P}(\mathcal{Z}\mid \mathcal{X})}{\mathcal{Q}(\mathcal{Z})}\right]d\mathcal{Z}\\ & =\text{ELBO}+\text{KL}[\mathcal{Q}(\mathcal{Z})||\mathcal{P}(\mathcal{Z}\mid \mathcal{X})]\end{array}$$
• 将证据下界($\text{Evidence of Lower Bound,ELBO}$)看作关于$\mathcal{Q}(\mathcal{Z})$的一个函数。称作$\mathcal{Q}(\mathcal{Z})$的变分($\text{Variation}$)。记作$\mathcal{L}[\mathcal{Q}(\mathcal{Z})]$：
  $$\begin{array}{r}\text{ELBO}={\int }_{\mathcal{Z}}\mathcal{Q}(\mathcal{Z})\cdot \left[\frac{\mathcal{P}(\mathcal{X},\mathcal{Z})}{\mathcal{Q}(\mathcal{Z})}\right]d\mathcal{Z}=\mathcal{L}[\mathcal{Q}(\mathcal{Z})]\end{array}$$
• 在随机梯度变分推断($\text{Stochastic Gradient Variational Inference, SGVI}$)的思路中，将条件概率分布$\mathcal{Q}(\mathcal{Z})$视作一个关于参数$\varphi$的函数形式$\mathcal{Q}(\mathcal{Z};\varphi )$，那么对应变分$\mathcal{L}[\mathcal{Q}(\mathcal{Z})]$也可描述成关于$\varphi$的函数形式：
  此时将求解分布$\mathcal{Q}(\mathcal{Z})$的问题转化为求解最优参数$\hat{\varphi }$的问题。
  $$\mathcal{L}[\mathcal{Q}(\mathcal{Z})]=\mathcal{L}[\mathcal{Q}(\mathcal{Z};\varphi )]\Rightarrow \mathcal{L}(\varphi )$$
  基于$\mathcal{L}(\varphi )$求解最大值，使用梯度上升($\text{Gradient Ascent,GA}$)方法近似求解。对应函数梯度表示如下：
  { ϕ ( t + 1 ) ⇐ ϕ ( t ) + η ∇ ϕ L ( ϕ ) ∇ ϕ L ( ϕ ) = E Q ( Z ; ϕ ) { ∇ ϕ log ⁡ Q ( Z ; ϕ ) ⋅ [ log ⁡ P ( X , Z ) − log ⁡ Q ( Z ; ϕ ) ] } \begin{cases} \phi^{(t+1)} \Leftarrow \phi^{(t)} + \eta \nabla_{\phi} \mathcal L(\phi) \\ \nabla_{\phi} \mathcal L(\phi) = \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left\{\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi) \cdot [\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)] \right\} \end{cases} {ϕ(t+1)⇐ϕ(t)+η∇ϕ​L(ϕ)∇ϕ​L(ϕ)=EQ(Z;ϕ)​{∇ϕ​logQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}​
• 在使用蒙特卡洛方法进行采样近似过程中，关于${\nabla }_{\varphi }\log \mathcal{Q}(\mathcal{Z};\varphi )$极容易出现高方差现象($\text{High Variance}$)，导致采样出的梯度结果${\nabla }_{\varphi }\mathcal{L}(\varphi )$极不稳定：
  $${\nabla }_{\varphi }\mathcal{L}(\varphi )\approx \frac{1}{N}\sum _{n=1}^N\left\{\underset{\text{High Variance}}{\underbrace{{\nabla }_{\varphi }\log \mathcal{Q}(z^{(n)};\varphi )}}\left[\log \mathcal{P}(\mathcal{X},z^{(n)})-\log \mathcal{Q}(z^{(n)};\varphi )\right]\right\}$$
  针对已经被视作函数的$\mathcal{Q}(\mathcal{Z};\varphi )$，通过重参数化技巧，通过构建一个 随机变量$ϵ$，使得$ϵ$与隐变量$\mathcal{Z}$之间存在如下函数关系：
  $$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X};\varphi )$$
  从而使得$ϵ$对应的概率分布$\mathcal{P}(ϵ)$与分布$\mathcal{Q}(\mathcal{Z};\varphi )$之间存在如下关系：
  E Q ( Z ; ϕ ) [ f ( Z ) ] = E P ( ϵ ) { f [ G ( ϵ , X ; ϕ ) ] } \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left[f(\mathcal Z)\right] = \mathbb E_{\mathcal P(\epsilon)} \left\{f[\mathcal G(\epsilon,\mathcal X;\phi)]\right\} EQ(Z;ϕ)​[f(Z)]=EP(ϵ)​{f[G(ϵ,X;ϕ)]}
  将上述关系带回原式，通过链式求导法则，可以表示成如下形式：
  • 将期望形式化简回积分形式。
  • 牛顿-莱布尼兹公式，将${\nabla }_{\varphi }$提到积分号前，后面再带回去。
  • 将$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X};\varphi )$代入，并将采样分布$\mathcal{Q}(\mathcal{Z};\varphi )$替换为$\mathcal{P}(ϵ)$.
    ∇ ϕ L ( ϕ ) = E Q ( Z ; ϕ ) { ∇ ϕ log ⁡ Q ( Z ; ϕ ) ⋅ [ log ⁡ P ( X , Z ) − log ⁡ Q ( Z ; ϕ ) ] } = ∇ ϕ ∫ Z Q ( Z ; ϕ ) ⋅ [ log ⁡ P ( X , Z ) − log ⁡ Q ( Z ; ϕ ) ] d Z = E P ( ϵ ) [ ∇ ϕ ( log ⁡ P ( X , Z ) − log ⁡ Q ( Z ; ϕ ) ) ] = E P ( ϵ ) [ ∇ Z ( log ⁡ P ( X , Z ) − log ⁡ Q ( Z ; ϕ ) ) ⋅ ∇ ϕ G ( ϵ , X ; ϕ ) ] \begin{aligned} \nabla_{\phi}\mathcal L(\phi) & = \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left\{\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi) \cdot [\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)] \right\} \\ & = \nabla_{\phi} \int_{\mathcal Z} \mathcal Q(\mathcal Z;\phi) \cdot \left[\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)\right] d\mathcal Z \\ & = \mathbb E_{\mathcal P(\epsilon)} \left[\nabla_{\phi}(\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi))\right] \\ & = \mathbb E_{\mathcal P(\epsilon)} [\nabla_{\mathcal Z}(\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)) \cdot \nabla_{\phi}\mathcal G(\epsilon,\mathcal X;\phi)] \end{aligned} ∇ϕ​L(ϕ)​=EQ(Z;ϕ)​{∇ϕ​logQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}=∇ϕ​∫Z​Q(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]dZ=EP(ϵ)​[∇ϕ​(logP(X,Z)−logQ(Z;ϕ))]=EP(ϵ)​[∇Z​(logP(X,Z)−logQ(Z;ϕ))⋅∇ϕ​G(ϵ,X;ϕ)]​

通过这种重参数化技巧——将 变量$\mathcal{Z}$ 与 简单分布对应变量$ϵ$ 之间构建关联关系的方式，仅需要从简单分布$\mathcal{P}(ϵ)$中进行采样，也可以采集出${\nabla }_{\varphi }\mathcal{L}(\varphi )$中的样本。

重参数化技巧(随机反向传播)介绍

关于神经网络，可以通过通用逼近定理($\text{Universal Approximation Theorem}$)来逼近任意函数。那么神经网络是否也可以用来 逼近概率分布 呢？
从概率图模型的视角，概率分布$\mathcal{P}(\mathcal{X})$就是概率图模型结构的表示($\text{Representation}$)。如果能够直接使用神经网络直接将$\mathcal{P}(\mathcal{X})$描述出来，就称之为随机反向传播($\text{Stochastic Backward Propagation}$)，也称重参数化技巧($\text{Reparametrization Trick}$)。

在上面关于变分推断——重参数化技巧的过程中，关于$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X};\varphi )$中的函数$\mathcal{G}$，同样可以描述成如下结构：

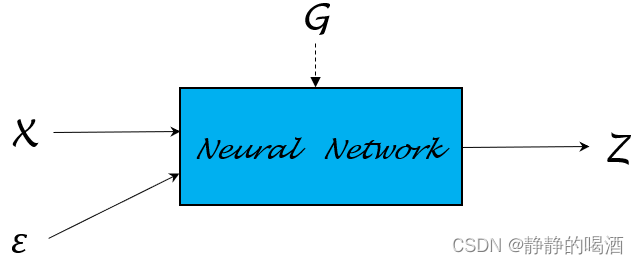
这里从简单的概率分布开始，观察如何使用重参数化技巧对概率分布进行描述的。

示例描述——联合概率分布

假设某随机变量$\mathcal{Y}$服从均值为$\mu$，方差为${\sigma }^2$的一维正态分布：
$$\mathcal{P}(\mathcal{Y})=\mathcal{N}(\mu ,{\sigma }^2)$$
如果直接从这个分布中进行采样，可能是复杂的。但是如果可以假定一个变量$\mathcal{Z}$服从标准正态分布$\mathcal{N}(0,1)$，并且$\mathcal{Y},\mathcal{Z}$之间满足如下关系：
$$\mathcal{Y}=\mu +\sigma \times \mathcal{Z}$$
那么则有：
该部分推导过程详见：变分推断——重参数化技巧
$${\mathbb{E}}_{\mathcal{P}(\mathcal{Y})}[f(\mathcal{Y})]={\mathbb{E}}_{\mathcal{P}(\mathcal{Z})}[f(\mu +\sigma \times \mathcal{Z})]$$
这种替换采样分布的操作意味着：在给定$\mathcal{Z}$分布的条件下，完全可以通过采样$\mathcal{Z}$分布，得到$\mathcal{Y}$分布的样本：
这里的${\mathcal{Z}}^{(i)},{\mathcal{Y}}^{(i)}$分别表示概率分布$\mathcal{P}(\mathcal{Z}),\mathcal{P}(\mathcal{Y})$中采集的样本。
$$\{\begin{array}{l}{\mathcal{Z}}^{(i)}\sim \mathcal{N}(0,1)\\ {\mathcal{Y}}^{(i)}=\mu +\sigma \times {\mathcal{Z}}^{(i)}\end{array}$$
重新观察$\mathcal{Y}=\mu +\sigma \times \mathcal{Z}$，这明显就是一个简单的一次函数。从广义的角度观察，可以将$\mathcal{Y},\mathcal{Z}$之间满足如下函数关系：
其中$\mathcal{Z}$在函数中表示变量;$\mu ,\sigma$在函数中表示权重参数。
$$\mathcal{Y}=f(\mathcal{Z};\mu ,\sigma )$$
这意味着：我们不否认变量$\mathcal{Y}$具有随机性，只不过变量$\mathcal{Y}$的随机性由变量$\mathcal{Z}$决定。也就是说，除了$\mathcal{Z}$的随机性，其他变量(这里指的$\mathcal{Y}$)都是确定性变换，那么完全可以使用神经网络对函数$f(\mathcal{Z};\mu ,\sigma )$进行逼近：

• 这里的‘确定性变换’是指：当变量$\mathcal{Z}$确定的条件下，那么变量$\mathcal{Y}$根据函数$f(\mathcal{Z};\mu ,\sigma )$也跟着确定。也就是说$\mathcal{Z},\mathcal{Y}$之间存在明确的映射关系。
• 使用神经网络逼近函数，完全不用担心原始函数中的参数$\mu ,\sigma$,因为被替代的神经网络权重参数$\theta$本身没有实际意义。
  
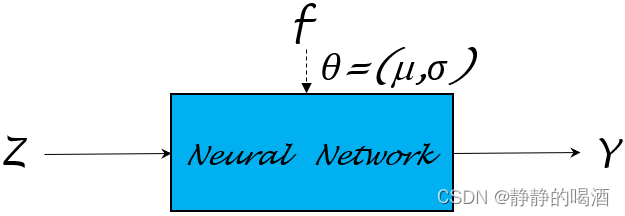
  如果定义$\mathcal{J}(\mathcal{Y})$为目标函数，在对目标函数求解极值的过程中，对模型参数$\theta$求解梯度。根据链式求导法则，梯度${\nabla }_{\theta }\mathcal{J}(\mathcal{Y})$ 可表示为如下形式：
  $$\{\begin{array}{l}\mathcal{J}(\mathcal{Y})=\mathcal{J}[f(\mathcal{Z};\mu ,\sigma )]\\ {\nabla }_{\theta }\mathcal{J}(\mathcal{Y})={\nabla }_{\mathcal{Y}}\mathcal{J}(\mathcal{Y})\cdot {\nabla }_{\theta }f(\mathcal{Z};\mu ,\sigma )\end{array}$$

示例描述——条件概率分布

假设给定随机变量$\mathcal{X}$条件下，随机变量$\mathcal{Y}$的条件概率分布满足如下关系：
$$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})=\mathcal{N}(\mu ,{\sigma }^2\mid \mathcal{X})$$
与上面描述对应，可以根据分布$\mathcal{N}(\mu ,{\sigma }^2\mid \mathcal{X})$，可以将随机变量$\mathcal{Y}$与随机变量$\mathcal{X}$之间描述成如下函数关系：
$$\{\begin{array}{l}\mathcal{Z}\sim \mathcal{N}(0,1)\\ \mathcal{Y}=\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}\end{array}$$
同样可以使用上述方法，对随机变量$\mathcal{Y}$与随机变量$\mathcal{Z}$之间的关系进行验证：

• 关键点1：从概率密度函数的角度观察，由于$\mathcal{X}$是条件，是已知量。因而可以将$\mathcal{N}(\mu ,{\sigma }^2\mid \mathcal{X})$看作是随机变量$\mathcal{X}$参与的概率密度函数:$\mathcal{N}[\mu (\mathcal{X}),{\sigma }^2(\mathcal{X})]$
• 证明期望${\mathbb{E}}_{\mathcal{P}(\mathcal{Y}\mid \mathcal{X})}[f(\mathcal{Y})]$转换成期望 E P ( Z ) { f [ μ ( X ) + σ ( X ) × Z ] } \mathbb E_{\mathcal P(\mathcal Z)} \{f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z]\} EP(Z)​{f[μ(X)+σ(X)×Z]}的过程实际上是描述$\mathcal{Y}$被替换成$\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}$后，其采样分布也会由$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})$转换成$\mathcal{P}(\mathcal{Z})$,而不仅仅是单纯意义上的替换。
• 关键点2：将$\mathcal{Y}=\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}$代入的过程中，由于是对$\mathcal{Z}$求解偏导，因而有$d\mathcal{Y}=d[\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}]=\sigma (\mathcal{X})d\mathcal{Z}$

E P ( Y ∣ X ) [ f ( Y ) ] = ∫ Y P ( Y ∣ X ) ⋅ f ( Y ) d Y = ∫ Y 1 σ ( X ) ⋅ 2 π exp ⁡ { − [ Y − μ ( X ) ] 2 2 σ 2 ( X ) } ⏟ N [ μ ( X ) , σ 2 ( X ) ] ⋅ f ( Y ) d Y = ∫ Z 1 σ ( X ) ⋅ 2 π exp ⁡ { − [ μ ( X ) + σ ( X ) × Z − μ ( X ) ] 2 2 σ 2 ( X ) } ⋅ f [ μ ( X ) + σ ( X ) × Z ] ⋅ σ ( X ) d Z ⏟ d [ μ ( X ) + σ ( X ) × Z ] = ∫ Z 1 2 π ⋅ exp ⁡ ( − Z 2 2 ) ⏟ P ( Z ) = N ( 0 , 1 ) ⋅ f [ μ ( X ) + σ ( X ) × Z ] d Z = ∫ Z P ( Z ) ⋅ f [ μ ( X ) + σ ( X ) × Z ] d Z = E P ( Z ) { f [ μ ( X ) + σ ( X ) × Z ] } \begin{aligned} \mathbb E_{\mathcal P(\mathcal Y \mid \mathcal X)} [f(\mathcal Y)] & = \int_{\mathcal Y} \mathcal P(\mathcal Y \mid \mathcal X) \cdot f(\mathcal Y) d\mathcal Y \\ & = \int_{\mathcal Y} \underbrace{\frac{1}{\sigma(\mathcal X) \cdot \sqrt{2\pi}}\exp \left\{-\frac{[\mathcal Y - \mu(\mathcal X)]^2}{2\sigma^2(\mathcal X)}\right\}}_{\mathcal N[\mu(\mathcal X),\sigma^2(\mathcal X)]} \cdot f(\mathcal Y) d\mathcal Y \\ & = \int_\mathcal Z \frac{1}{\sigma(\mathcal X) \cdot \sqrt{2\pi}} \exp \left\{-\frac{[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z - \mu(\mathcal X)]^2}{2\sigma^2(\mathcal X)}\right\} \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] \cdot \underbrace{\sigma(\mathcal X) d\mathcal Z}_{d[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z]} \\ & = \int_{\mathcal Z} \underbrace{\frac{1}{\sqrt{2\pi}} \cdot \exp \left(-\frac{\mathcal Z^2}{2}\right)}_{\mathcal P(\mathcal Z) = \mathcal N(0,1)} \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] d\mathcal Z \\ & = \int_{\mathcal Z}\mathcal P(\mathcal Z) \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] d\mathcal Z \\ & = \mathbb E_{\mathcal P(\mathcal Z)} \{f[\mu(\mathcal X) +\sigma(\mathcal X) \times \mathcal Z]\} \end{aligned} EP(Y∣X)​[f(Y)]​=∫Y​P(Y∣X)⋅f(Y)dY=∫Y​N[μ(X),σ2(X)] σ(X)⋅2π ​1​exp{−2σ2(X)[Y−μ(X)]2​}​​⋅f(Y)dY=∫Z​σ(X)⋅2π ​1​exp{−2σ2(X)[μ(X)+σ(X)×Z−μ(X)]2​}⋅f[μ(X)+σ(X)×Z]⋅d[μ(X)+σ(X)×Z] σ(X)dZ​​=∫Z​P(Z)=N(0,1) 2π ​1​⋅exp(−2Z2​)​​⋅f[μ(X)+σ(X)×Z]dZ=∫Z​P(Z)⋅f[μ(X)+σ(X)×Z]dZ=EP(Z)​{f[μ(X)+σ(X)×Z]}​
同理，基于上述的神经网络描述，同样也可以随机变量$\mathcal{X},\mathcal{Z}\sim \mathcal{N}(0,1)$为输入，$\mathcal{Y}$作为输出，学习并逼近函数$\mathcal{Y}=\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}$：

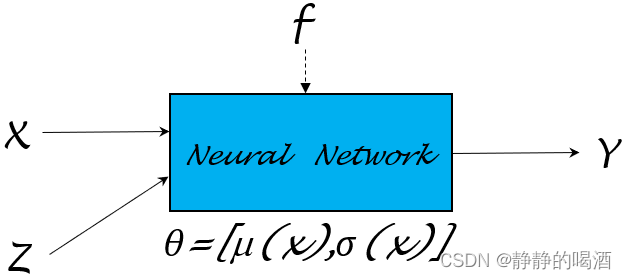
继续向下观察。从$\mathcal{Y}=\mu (\mathcal{X})+\sigma (\mathcal{X})\times \mathcal{Z}$中可以观察到：

• $\mathcal{Y}$是关于$\mathcal{Z}$的函数，其中参数是$\mu (\mathcal{X}),\sigma (\mathcal{X})$；
• 而$\mu ,\sigma$均是关于$\mathcal{X}$的函数。

既然$\mu ,\sigma$函数均以随机变量$\mathcal{X}$作为输入，这里将这两个函数的参数统一描述成$\theta$。即：$\mu (\mathcal{X};\theta ),\sigma (\mathcal{X};\theta )$。这种变换意味着：仅通过学习模型参数$\theta$，就可以将$\mu (\mathcal{X}),\sigma (\mathcal{X})$均给表示出来。上述神经网络结构可细化成如下形式：
其中$\odot$表示点乘;$\oplus$表示数学加法。

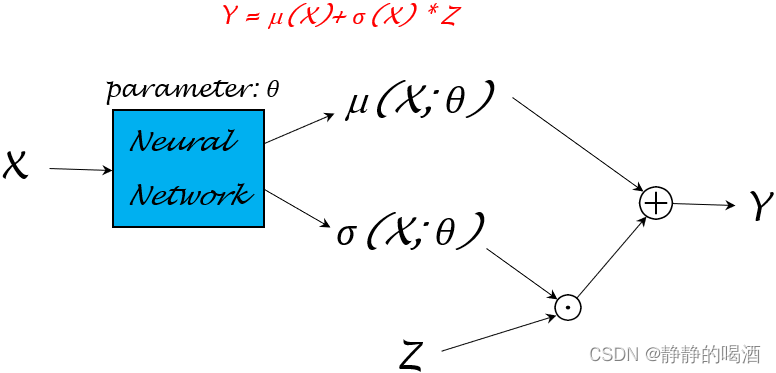
关于模型参数$\theta$的参数学习过程可以很灵活。关于函数$\mu (\mathcal{X}),\sigma (\mathcal{X})$可以再详细分成不同的模型参数$\mu (\mathcal{X};\theta ),\sigma (\mathcal{X};\varphi )$进行学习：
神经网络仅是一个‘函数逼近器’的作用，如何将模型参数学习的更好，可以有很深的挖掘空间。只不过这里我们事先知道$\mathcal{Y}$的分布是$\mathcal{N}(\mu ,\sigma \mid \mathcal{X})$,这里的$\mu ,\sigma$被赋予了实际意义。但真实情况是，这个条件概率分布$\mathcal{Y}$可能非常复杂。我们对模型参数组成可能一无所知。

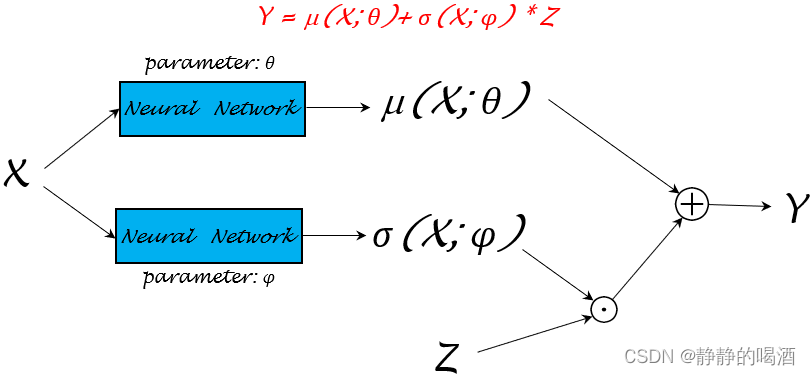
同样可以构建一个目标函数$\mathcal{J}(\mathcal{Y})$，通过链式求导法则，将对应的模型参数梯度进行求解。
示例：如果通过重参数化技巧产生样本所代表的概率分布${\mathcal{Y}}_{pred}$与真实分布$\mathcal{Y}$之间的差距(可以看成一个基于分布的回归任务)，可以通过最小二乘估计对差距进行描述：

• 这里以第一种模型结构为例。
• 其中${\mathcal{Y}}_{gene}^{(i)}$就是图中$\mathcal{Y}$通过上述模型结构产生的一个样本(幻想粒子)，与对应真实分布中的${\mathcal{Y}}^{(i)}$样本进行比较。
  $$\mathcal{J}({\mathcal{Y}}_{gene};\theta )=\sum _{i=1}^N||{\mathcal{Y}}_{gene}^{(i)}-{\mathcal{Y}}^{(i)}|{|}^2$$
  对应梯度${\nabla }_{\theta }\mathcal{J}({\mathcal{Y}}_{gene};\theta )$可表示为：
  $${\nabla }_{\theta }\mathcal{J}({\mathcal{Y}}_{gene};\theta )=\begin{array}{r}\frac{\partial \mathcal{J}({\mathcal{Y}}_{gene};\theta )}{\partial {\mathcal{Y}}_{gene}}\cdot \frac{\partial {\mathcal{Y}}_{gene}}{\partial \mu (\mathcal{X};\theta )}\cdot \frac{\partial \mu (\mathcal{X};\theta )}{\partial \theta }+\frac{\partial \mathcal{J}({\mathcal{Y}}_{gene};\theta )}{\partial {\mathcal{Y}}_{gene}}\cdot \frac{\partial {\mathcal{Y}}_{gene}}{\partial \sigma (\mathcal{X};\theta )}\cdot \frac{\partial \sigma (\mathcal{X};\theta )}{\partial \theta }\end{array}$$

总结

通过上面的描述，通过重参数化技巧构造神经网络去逼近联合概率分布、条件概率分布。关于这种表示方式，对于生成分布$\mathcal{Y}$是存在约束条件的。即：$\mathcal{Y}$是一个 连续分布。这才能使$\frac{\partial {\mathcal{Y}}_{gene}}{\partial \mu (\mathcal{X};\theta )},\frac{\partial {\mathcal{Y}}_{gene}}{\partial \sigma (\mathcal{X};\theta )}$有解。

至此，生成模型部分介绍结束，下一节将介绍流模型($\text{Flow-based Model}$)。

相关参考：
生成模型6-重参数化技巧(随机后向传播)