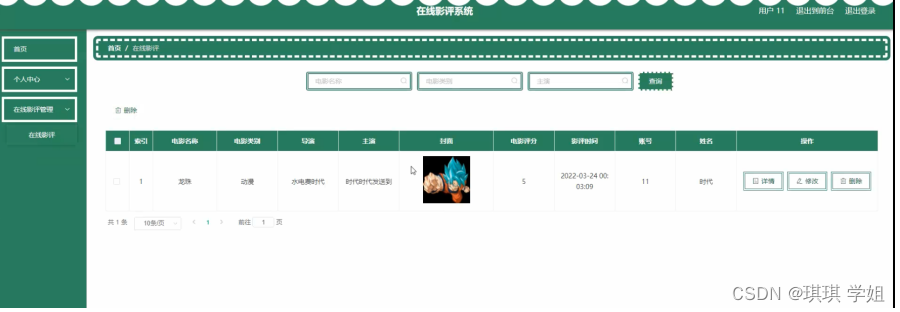
问题描述
中国古代数学家张邱建在他的《算经》中提出了一个著名的“百钱百鸡问题”:一只公鸡值五钱,一只母鸡值三钱,三只小鸡值一钱,现在要用百钱买百鸡,请问公鸡、母鸡、小鸡各多少只?
分析
这也是经典问题了,在数学上其实不过就是多元一次方程组。如果用cock代表公鸡的数量,hen代表母鸡,chicken代表小鸡,可列出方程组如下:
如果使用计算机思维,因为数据量小(小于100),完全可以用穷举法,使用三层嵌套循环,从外向内分别代表公鸡、母鸡、小鸡的数量,然后依次判断三者的值是否同时满足上述两个方程。
因为100钱最多可以买只公鸡,
只母鸡,
只小鸡,所以这三个变量的上限分别是20、33、300。但同时又不能把钱全部用来买公鸡、母鸡、小鸡——因为数量不对,所以取值分别最多为19、32、297(小鸡的数量要能被3整除)于是可编写代码如下:
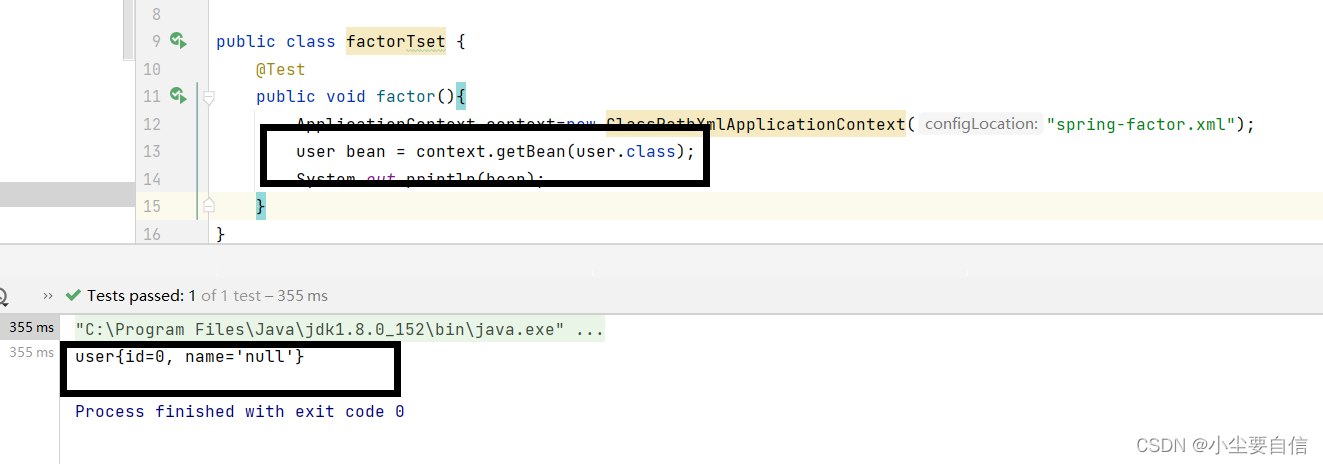
for cock in range(20):
for hen in range(33):
for chicken in range(298):
if cock+hen+chicken=100 and 5*cock+3*hen+chicken/3==100:
print(f"可买{cock}只公鸡,{hen}只母鸡,{chicken}只小鸡"当然,这只是最基本的计算机思维下的穷举法,如果我们稍微代入一点数学知识,就会发现cock、hen、chicken三者中的任一个都可以由另外两个得到,比如,所以完全用不到三层循环,只要知道cock和hen,就可以根据方程1得到chicken的数量。此外,由于chicken的上限最大(297),消灭chicken的循环将能最大减少循环次数,提高效率,于是,可以修改代码如下:
for cock in range(20):
for hen in range(33):
chicken = 100-cock-hen
if 5*cock+3*hen+chicken/3==100:
print(f"可买{cock}只公鸡,{hen}只母鸡,{chicken}只小鸡"得到的答案是一样的,说明程序实现的效果相同,但效率大为提升。
但这还没完。
通过数学思维,我们可以进一步发现,将等式2两边都乘以3,再减去等式1,就可以把变量chicken消去,
得到一个新的等式:
两边再同时除以2,得到:
于是就可以从公鸡的数量得到母鸡的数量:,进而把第二层循环也可以省去了。
同时,观察这个母鸡的等式,右边是公鸡的数量除以4,而常识告诉我们,母鸡的数量必须
- 是整数
- 大于0
于是,cock的数量必须是4的整数倍,而且。而cock的数量本身也必须是整数,所以cock的取值范围就是
因此,我们可以编写代码,仅仅对这个范围的cock数量进行穷举,数量大大减少,0、4、8、12,计算效率大大提高。唯一需要注意的是,因为引入了除法(7/4),得到的结果自动变成浮点型数据,即使能整除,得到的结果显示出来也是x.0的样子。而我们要输出整数,所以这里可以使用int()把计算结果转成整数型,或者,直接使用整除运算符(//)。
for cock in range(0,14,4):
hen = 25-int(cock*7/4):
chicken = 100-cock-hen
if 5*cock+3*hen+chicken/3==100:
print(f"可买{cock}只公鸡,{hen}只母鸡,{chicken}只小鸡"输出
可买0只公鸡,25只母鸡,75只小鸡
可买4只公鸡,18只母鸡,78只小鸡
可买8只公鸡,11只母鸡,81只小鸡
可买12只公鸡,4只母鸡,84只小鸡其实,当我们使用数学知识手动完成上面的计算后,得到的解(公鸡数量0、4、8、12)必然就是合理解了,无需再进行验证,由此可见,在这里使用代码反而显得画蛇添足、多此一举了。这便是计算机思维和数学思维的区别。计算机思维看似简单,但胜在运算速度,而数学思维总是可以更巧妙地找到更快解决问题的办法,有时甚至都不需要用到计算机思维。而我们要做的,就是在面对不同问题的时候,将二者结合起来,取长补短,争取以最高的效率解决问题。