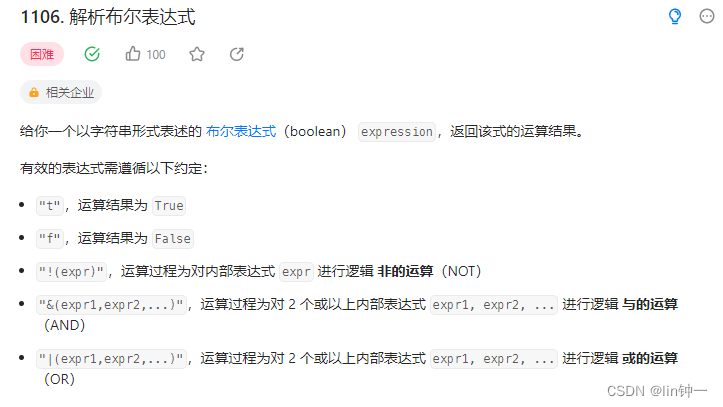
题目链接:点击跳转
思路
方法一、DFS模拟栈
题目意思很简单让你去判断与或非布尔表达式的结果,我们可以看布尔表达式看成一棵树,需要我们解决的是从最底层的嵌套布尔表达式产生的结果不断向上的结果,如图:
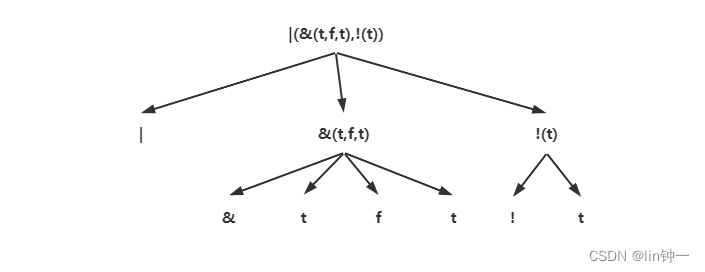
既然他是一棵树且我需要从叶结点往上,肯定能看出来直接用DFS遍历树不就好了吗,接下来要解决的问题就是怎么区分他的每个结点:
- 如果是
t、r则我们直接返回结果。 - 在
&、|布尔表达式中存在多个结点(内部表达式),每个结点(内部表达式)用,分割,需要注意我们不能直接用,来区分,因为可能存在嵌套的子树(内部表达式)那表达式怎么区分呢?- 其实仔细一看这不就是括号匹配么 ,我们用栈不就可以解决了么!
- 所以我们只需要建立两个变量
lcnt,rcnt分别表示左括号数量和右括号数量- 如果 lcnt - 1 == rcnt,表示当前这个内部表达式是一颗嵌套的子树。用DFS递归去解决
- 如果 lcnt == rcnt,表示我们这个内部表达式已经结束了,用DFS递归去解决最后一个结点即可,将产生的结果向上传递返回。
- 在&的布尔表达式中,如果出现了一个false那整个表达式就是false,我们可以用标记记录即可。
- 在|的布尔表达式中,如果出现了一个true那整个表达式就是true,我们可以用标记记录即可。
- 剩下的细节完善一下即可。
代码示例
func parseBoolExpr(s string) bool {
if s[0] == 't' {
return true
} else if s[0] == 'f' {
return false
} else if s[0] == '!' {
if parseBoolExpr(s[2:]) {
return false
} else {
return true
}
} else if s[0] == '&' {
l, r, lcnt, rcnt, f := 2, 2, 1, 0, 1
for lcnt != rcnt && r < len(s) {
if s[r] == ',' && lcnt-1 == rcnt {
if !parseBoolExpr(s[l:r]) {
f = 0
}
l = r + 1
} else if s[r] == '(' {
lcnt++
} else if s[r] == ')' {
rcnt++
if lcnt == rcnt {
if !parseBoolExpr(s[l:r]) {
f = 0
}
}
}
r++
}
if f == 1 {
return true
} else {
return false
}
} else if s[0] == '|' {
l, r, lcnt, rcnt, f := 2, 2, 1, 0, 0
for lcnt != rcnt && r < len(s) {
if s[r] == ',' && lcnt-1 == rcnt {
if parseBoolExpr(s[l:r]) {
f = 1
}
l = r + 1
} else if s[r] == '(' {
lcnt++
} else if s[r] == ')' {
rcnt++
if lcnt == rcnt {
if parseBoolExpr(s[l:r]) {
f = 1
}
}
}
r++
}
if f == 1 {
return true
} else {
return false
}
}
return true
}
复杂度分析
- 时间复杂度:O(n),其中n表示 s 字符串的长度,遍历一遍字符串需要O(n)的时间。
- 空间复杂度:O(1),不需要申请额外的空间