在一个软件项目中,管理人员需要按时了解项目进度,制定项目计划,同时需要及时发现所遇到的问题,然后和团队成员制定解决方案,确保整个计划可以顺利的进行,因此项目进度安排与跟踪是项目管理中的一个重要环节。
一、项目进度安排的定义及原则
1、进度安排的定义
项目进度安排,即通过将工作量分配给特定的软件工程任务,和将所估算的工作量分布于已经计划好的项目持续时间中。
2、进度安排的基本原则
(1)划分 —— 项目被划分为若干个可管理的活动和任务;
(2)相互依赖 —— 活动和任务之间的关系必须被确定为:顺序、并发、后续、独立进行;
(3)时间分配 —— 为每个任务分配工作单位(即开始和结束时间);
(4)工作量确认 —— 确保在任意时段分配到任务的人员数量不会超过项目组的人员数量;(比如:一个项目组此次预估需要有12人分配到任务才能完成此项工作,但原定人员数量为10人,那么12>10,这项任务的工作量必然超标了,所以要确保不能超过);
(5)定义责任 —— 每个被调度的任务都应该指定负责人;
(6)定义结果 —— 每个被调度的任务都要有一个定义好的输出结果;
(7)定义里程碑 —— 每个任务或任务组都与一个项目里程碑相关联;
二、通信开销
1、通信开销的定义
当几个人共同承担软件开发任务时,人与人之间必须通过交流来解决各自承担任务之间的接口问题,即所谓通信问题。通信需花费时间和代价,会引起软件错误增加,降低软件生产率。
2、通信路径计算
如果一个软件开发小组有 n 个人,每两人之间都需要通信,则总的通信路径有 条。
如想对通信路径有进一步了解,可到项目管理中的4P文章中的项目小组结构进行查看
3、案例分析
Q1:设一个人单独开发软件,生产率是5000行/人年。若 4 个人组成一个小组共同开发这个软件,则需要 6条通信路径。若在每条通信路径上耗费的工作量是 250 行/人年。则小组中每个人的软件生产率降低为多少?
A1:小组中每个人的软件生产率降低为 5000 - ×250 = 5000 - 375 = 4625 行/人年,所以项目组的生产率为18500。
Q2:如在上例中,到了开发后期再加入两名工程师,生产率为840行/人年,问此时项目组的生产率为?
A2:6个人所产生的的通信路径为 = 15条;所以项目组的生产率为5000 × 4 + 840 × 2 - 15 × 250 = 17930。
从上述分析可知:
一个软件任务由一个人单独开发,生产率最高;而对于一个稍大型的软件项目,一个人单独开发,时间又太长;因此软件开发小组是必要的。
但是,开发小组不宜太大,成员之间要避免过多的通信路径。
在开发进程中,切忌中途加人,避免不必要的的生产率损失。
三、工作量分配
1、40-20-40规则
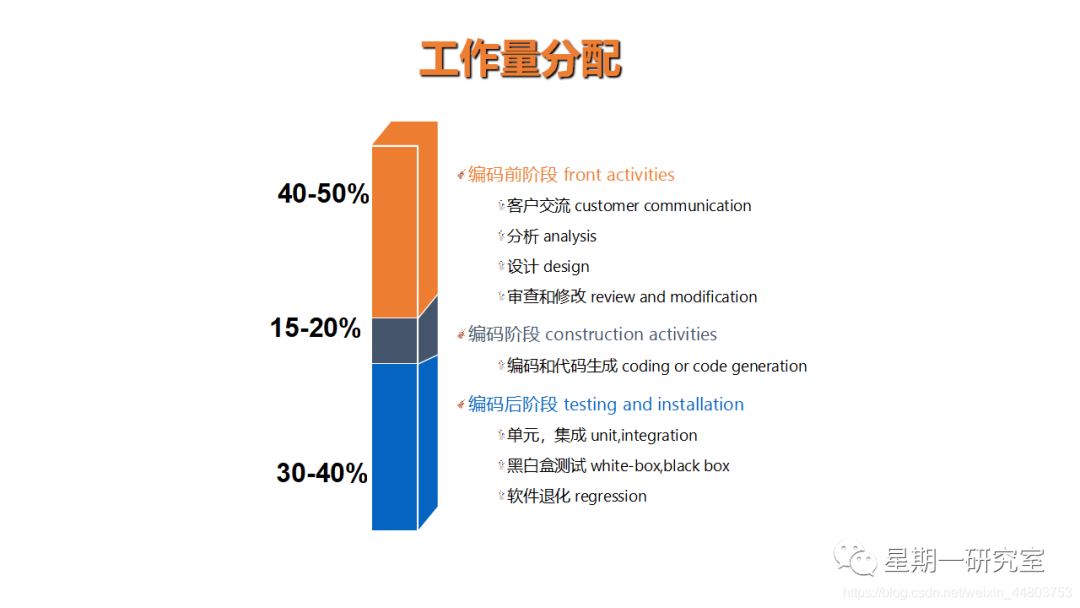
(1)在整个软件开发过程中,编码工作量仅占 20%,编码前工作量占40%,编码后工作量占 40%。
(2)40-20-40 规则只应用来作为一个指南,实际的工作量分配比例必须按照各项目的特点来决定。
2、工作量分配图例
用一张图来了解关于软件各阶段的工作量分配比例。
3、工作量分布推荐
在实际的软件开发中,一种比较推荐的工作量分布为:
计划阶段planning -> 2-3% ;
需求分析阶段requirements analysis -> 10-25 % ;
设计阶段design -> 20-25 %;
编码阶段coding -> 15-20 % ;
测试和调试阶段testing and debugging -> 30-40 % 。
四、项目进度安排方法
1、关键路径方法(CPM,Critical Path Method)
(1)定义
在关键路径上的活动才是按时完成任务的关键。
(2)关键路径的相关表达
LS:Latest start time 最晚开始时间;
ES:Earliest start time 最早开始时间;
FT:Float Time 浮动时间;
关键路径的判断:计算哪条路径最长,即为关键路径;
关键路径上的节点对应的浮动时间为FT = 0,且在每个项目中,关键路径不止一条;
如果关键路径上的活动开始时间推迟,将会直接影响工期;
最晚开始时间 - 最早开始时间 = 浮动时间。
(3)案例分析:盖房子
表1 盖一所房子的重要阶段
阶段 | 完成事项 |
1.1 | 完成调查 |
1.2 | 签发许可证 |
1.3 | 完成挖掘 |
1.4 | 库存材料 |
2.1 | 施工地基 |
2.2 | 外墙完成 |
2.3 | 外部管道完成 |
2.4 | 外部电力工作完成 |
2.5 | 外部壁板完成 |
2.6 | 外部涂装完成 |
2.7 | 安装门和一些固定设施 |
2.8 | 屋顶完成 |
3.1 | 内部管道完成 |
3.2 | 内部电力工作完成 |
3.3 | 墙板就位 |
3.4 | 内部涂装完成 |
3.5 | 铺设地板 |
3.6 | 安装门和一些固定设施 |
表2 盖房子相关活动的时间估计
具体活动 | 估计时间(天) |
Step1: 准备工作 | |
完成调查 | 3 |
签发许可证 | 15 |
完成挖掘 | 10 |
库存材料 | 10 |
Step2: 构建外部 | |
施工地基 | 15 |
外墙完成 | 20 |
外部管道完成 | 10 |
外部电力工作完成 | 10 |
外部壁板完成 | 8 |
外部涂装完成 | 5 |
安装门和一些固定设施 | 6 |
屋顶完成 | 9 |
Step3: 构建内部 | |
内部管道完成 | 12 |
内部电力工作完成 | 15 |
墙板就位 | 9 |
内部涂装完成 | 18 |
铺设地板 | 11 |
安装门和一些固定设施 | 7 |
表3 任务网络图
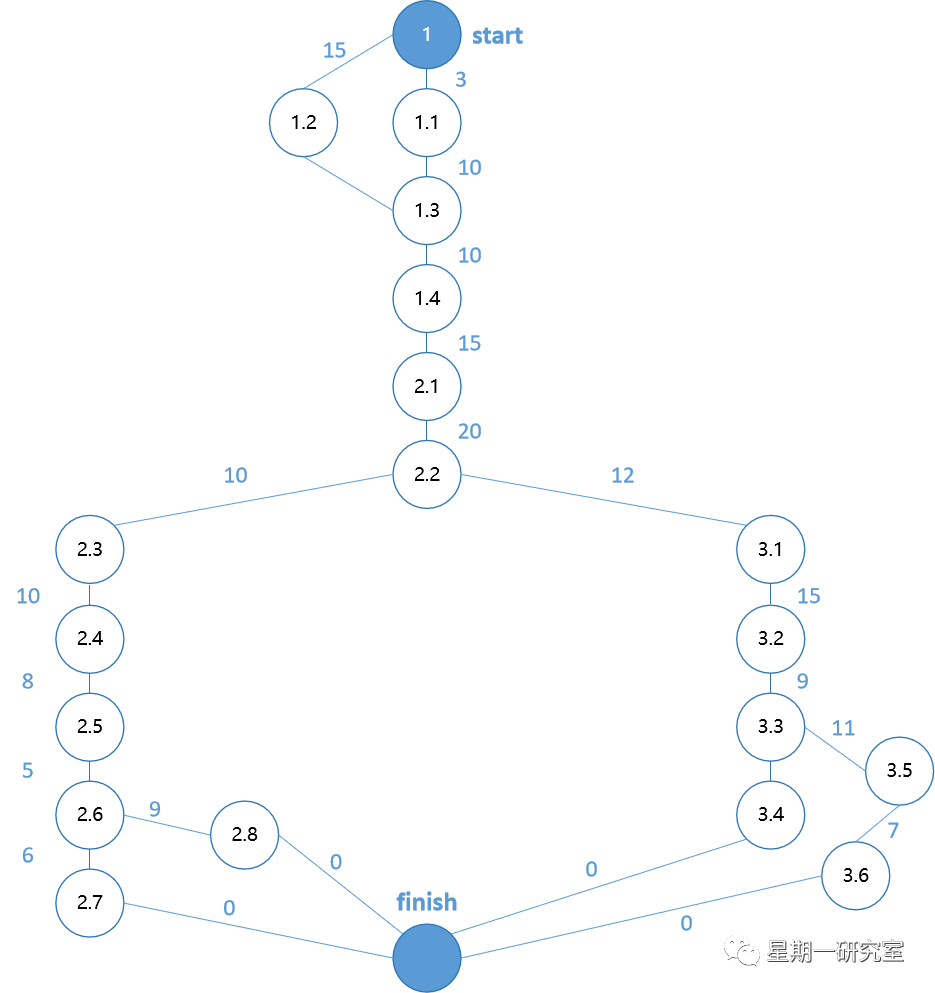
问:某项目的活动网络图如表3所示,每项活动所需的天数如路径上数字所示。(1)请给出计算过程确定项目的关键路径和工期。(2)设定活动1.1和1.2的最早开始时间均为第1天,给出所有活动的最早开始时间ES、最迟开始时间LS和浮动时间FT。
答案解析:
(1)从图中可以看出,该项目有8条路径可以走到终点,分别为:
①start → 1.1(3) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 2.3(10) → 2.4(10) → 2.5(8) → 2.6(5) → 2.7(6) → finish;
②start → 1.1(3) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 2.3(10) → 2.4(10) → 2.5(8) → 2.6(5) → 2.8(9) → finish;
③start → 1.1(3) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 3.1(12) → 3.2(15) → 3.3(9) → 3.4(18) → finish;
④start → 1.1(3) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 3.1(12) → 3.2(15) → 3.3(9) → 3.5(11) → 3.6(7) → finish;
⑤start → 1.2(15) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 2.3(10) → 2.4(10) → 2.5(8) → 2.6(5) → 2.7(6) → finish;
⑥start → 1.2(15) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 2.3(10) → 2.4(10) → 2.5(8) → 2.6(5) → 2.8(9) → finish;
⑦start → 1.2(15) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 3.1(12) → 3.2(15) → 3.3(9) → 3.4(18) → finish;
⑧start → 1.2(15) → 1.3(10) →1.4(10) → 2.1(15) → 2.2(20) → 3.1(12) → 3.2(15) → 3.3(9) → 3.5(11) → 3.6(7) → finish。
8条路径如下图所示:
可以计算出,每条路径的工期分别为:
①3+10+10+15+20+10+10+8+5+6=97天;
②3+10+10+15+20+10+10+8+5+9=100天;
③3+10+10+15+20+12+15+9+18=112天;
④3+10+10+15+20+12+15+9+11+7=112天;
⑤15+10+10+15+20+10+10+8+5+6=109天;
⑥15+10+10+15+20+10+10+8+5+9=112天;
⑦15+10+10+15+20+12+15+9+18=124天;
⑧15+10+10+15+20+12+15+9+11+7=124天。
综上所述,项目的关键路径有两条,分别为⑦和⑧,即1.2 → 1.3 →1.4 → 2.1 → 2.2 → 3.1 → 3.2 → 3.3 → 3.4 和 1.2 → 1.3 →1.4 → 2.1 → 2.2 → 3.1 → 3.2 → 3.3 → 3.5 → 3.6,工期为124天。
(2)计算步骤如下:
①填充关键路径的浮动时间。已知关键路径的浮动时间都为0,所以路径⑦和⑧上的所有节点的浮动时间都为0;
②计算剩余节点的浮动时间。
由图可得,1.1 → 1.3需要时间为13天,而关键路径1.2 → 1.3需要25天,所以1.2的浮动时间为12天;
关键路径的前半部分为1.2 → 1.3 →1.4 → 2.1 → 2.2,后半部分有4个分路,⑦和⑧为关键路径,且后半部分的工期为54天;(12+15+9+18=54天,12+15+9+11+7=54天)
⑤和⑥的后半部分与关键路径的差额分别为54-39=15天,54-42=12天,那么此时可以确定2.7的浮动时间为15天,2.8的浮动时间为12天;(10+8+5+6=39天,10+8+5+9=42天)
由图可知,2.7和2.8都需要经过2.3 → 2.4 → 2.5 → 2.6,在这种情况下,选择与关键路径差额小的值为浮动时间,即2.3 → 2.4 → 2.5 → 2.6与2.8的浮动时间相等。
③计算最早开始时间。将每一项活动前面经过的路径(不包含当前活动)进行相加,如遇到分叉口则选择有经过关键路径上的节点。
④计算最迟开始时间。逆推,通过公式最晚开始时间 - 最早开始时间 = 浮动时间推出最迟开始时间。
项目活动的最早开始时间ES、最迟开始时间LS和浮动时间FT如下:
由上述案例可以得出,通过关键路径可以判断出:
开发时哪些活动必须等待;
开发时哪些活动必须按进度进行防止拖延问题发生。
2、项目(进度计划)评估和评审技术(PERT,Program Evaluation and Preview Technique)
(1)定义
项目评估和评审技术是一种关键路径分析技术,使用正态分布来判断一个活动的最早开始时间接近该活动进度时间的概率。PERT技术可以计算关键路径、找出最可能成为瓶颈的活动。
五、获得值分析
获得值分析,主要分析两个内容:①进度是否拖延;②成本是否超出预算。基于这两个内容,对获得值分析进行以下阐述。
1、基本量
(1)计划工作的预计成本(BCWS):截止到某一时刻,计划工作的预计工作量之和。
(2)完成预算(BAC):BCWS的总量,是项目的总工作量的估计。
(3)预定完成百分比:计划工作的预计成本占预计总工作量的百分比,计算公式为: 。
(4)完成工作的预计成本(BCWP):截止到某一时刻,完成工作的预计工作量之和。
(5)完成百分比:完成工作的预计成本占预计总工作量的百分比,计算公式为: 。
(6)所完成工作的实际成本(ACWP):截止到某一时刻,已完成的工作任务的实际工作量之和。
2、进度指示计算公式
(1)进度性能指标(SPI) = ;
(2)进度偏差(SV) = BCWP - BCWS;
(3)成本性能指标(CPI) = ;
(4)成本偏差(CV) = BCWP - ACWP。
总结:
当SPI > 1,SV > 0,进度超前;
当SPI = 1,SV = 0,进度正好;
当SPI < 1,SV < 0,进度落后;
当CPI > 1,CV > 0,成本节省;
当CPI = 1,CV = 0,成本正好;
当CPI < 1,CV < 0,成本超出预算。
3、案例分析
(1)案例一
下图是某工程的实际完成表。
工作任务 | 估计工作量 | 实际工作量 | 估计完成日期 | 实际完成日期(月日年) |
1 | 5 | 10 | 1/25/21 | 2/1/21 |
2 | 25 | 20 | 2/15/21 | 2/15/21 |
3 | 120 | 80 | 5/15/21 | |
4 | 40 | 50 | 4/15/21 | 4/1/21 |
5 | 60 | 50 | 7/1/21 | |
6 | 80 | 70 | 9/1/21 |
Question:在该工程实施过程中,截止到21年4月1号,进度是否拖延?工期是否超出预算?
Answer:
截止到21年4月1号,计划完成任务1、2,实际完成了1、2、4,由此可计算出 BCWS 、 BCWP 、 ACWP 和 BAC 的值。
计划工作的预计成本 BCWS 为:5 + 25 = 30
完成工作的预计成本 BCWP 为:5 + 25 + 40 = 70
所完成工作的实际成本 ACWP 为:10 + 20 + 50 = 80
完成预算 BAC 为:5 + 25 + 120 + 40 + 60 + 80 = 330
那么预定完成百分比为:
实际完成百分比为:
进度性能指标 SPI 为:
进度偏差 SV 为:
成本性能指标 CPI 为:
成本偏差 CV 为:
综上所述,因为 SPI > 1,SV > 0 , CPI < 1,CV < 0 ,所以截止到21年4月1日,该工程进度超前,成本超出预算。
(2)案例二
工作任务 | 估计工作量 | 实际工作量 | 估计完成日期 | 实际完成日期(月日年) |
1 | 50 | 70 | 1/25/21 | 2/1/21 |
2 | 35 | 20 | 2/15/21 | 2/15/21 |
3 | 20 | 40 | 2/25/21 | 3/1/21 |
4 | 40 | 40 | 4/15/21 | 4/1/21 |
5 | 60 | 10 | 6/1/21 | |
6 | 80 | 20 | 7/1/21 |
Question:若考察点在21年5月1日,此时任务完成进度如上图所示,问进度是否拖延?工期是否超出预算?
Answer:
截止到21年5月1号,计划完成任务1、2、3、4,实际完成了1、2、3、4,由此可计算出 BCWS 、 BCWP 、 ACWP 和 BAC 的值。
计划工作的预计成本 BCWS 为:50 + 35 + 20 + 40 = 145
完成工作的预计成本 BCWP 为:50 + 35 + 20 + 40 = 145
所完成工作的实际成本 ACWP 为:70 + 20 + 40 + 40 = 170
完成预算 BAC 为:50 + 35 + 20 + 40 + 60 + 80 = 285
那么预定完成百分比为:
实际完成百分比为:
进度性能指标 SPI 为:
进度偏差 SV 为:
成本性能指标 CPI 为:
成本偏差 CV 为:
综上所述,因为 SPI = 1,SV = 0 , CPI < 1,CV < 0 ,所以截止到21年4月1日,该工程进度正好,即项目按计划进行,但成本超出预算。
(3)案例三
Question:
你被指定负责一个软件项目,这个项目由4个部分(A、B、C、D)组成,项目总预算为53000元,其中A任务预算为26000元,B任务预算为12000元,C任务预算为10000元,D任务预算为5000元。
截止到8月31日,A任务已经全部完成,B任务过半,C任务刚开始,D任务还没有开始,下表给出截止到8月31日的计划成本和实际成本,采用50/50规则计算截止到8月31日为止的 CV , SV , CPI , SPI 。
任务 | 计划费用 BCWS(元) | 实际花费 ACWP(元) | 已获取价值 BCWP(元) |
A | 26000 | 25500 | 26000 |
B | 9000 | 5400 | 6000 |
C | 4800 | 4100 | 5000 |
D | 0 | 0 | 0 |
总计 | 39800 | 35000 | 37000 |
(备注:50/50规则指项目一开始就实现一半价值,直到结束才实现全部价值,即完成1%或99%,都认为只实现一半价值)
Answer:
截止到8月31日为止的 CV , SV , CPI , SPI 的计算结果如下:
CV=
SV=
AC=3500
SPI= 93%
CPI= 106%
综上所述,因为 SPI < 1,SV < 0 , CPI > 1,CV > 0 ,所以截止到8月31日,该工程进度落后一些,但是费用节省了。
通过一道关键路径法例题全面解析关键路径的算法,例题详见下图
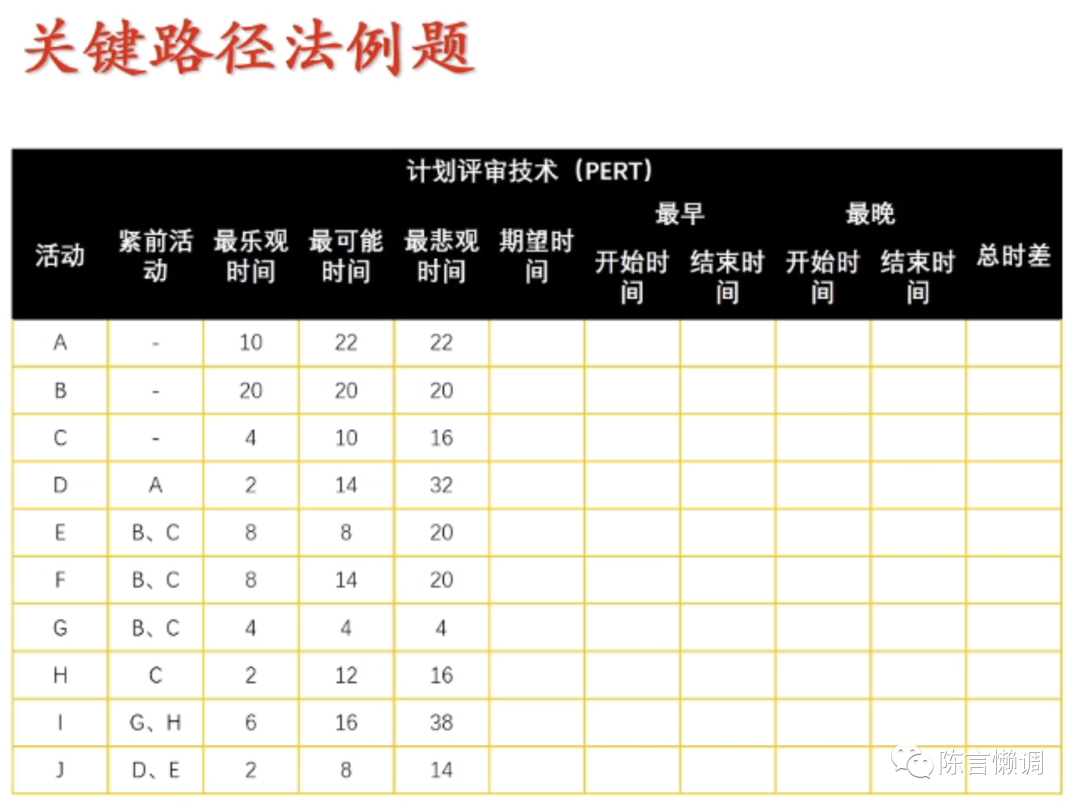
第一步、画出进度网络图
根据例题可以看出,A、B、C没有紧前活动,那么A、B、C为开始活动,E、F、G的紧前活动为B和C,H的紧前活动为C,I的紧前活动为G、H,J的紧前活动为D、E,由此可得出,F、I、J为结束活动(没有紧后活动),由此画出下图
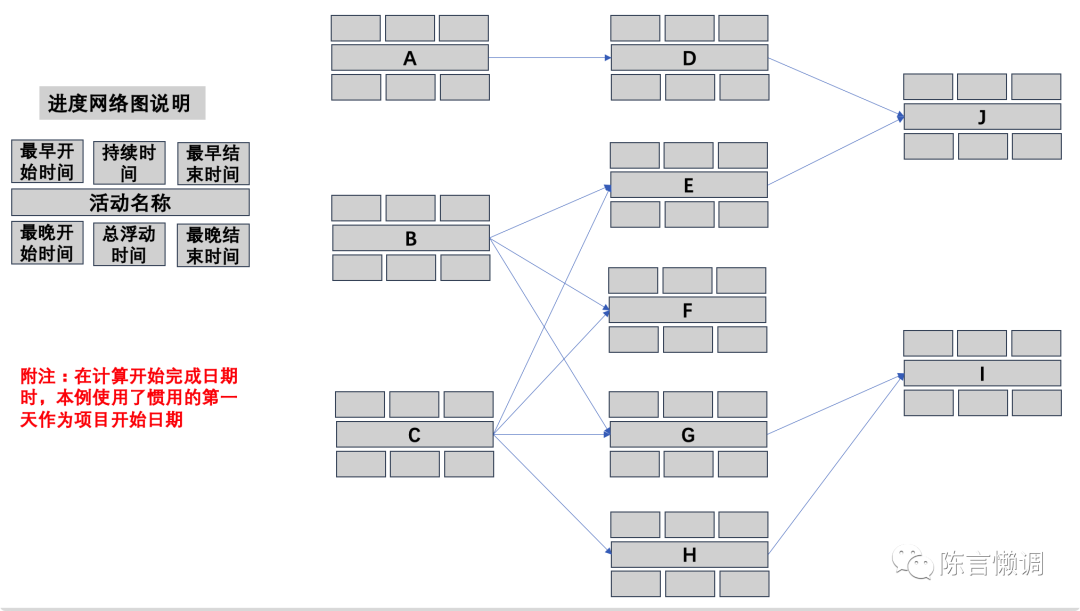
第二步、遍历路径
根据最乐观时间、最悲观时间、最可能时间,利用三点估算中的beta算法,期望值=(最乐观的时间+最可能的时间*4+最悲观的时间)/6,可以得出以下图示
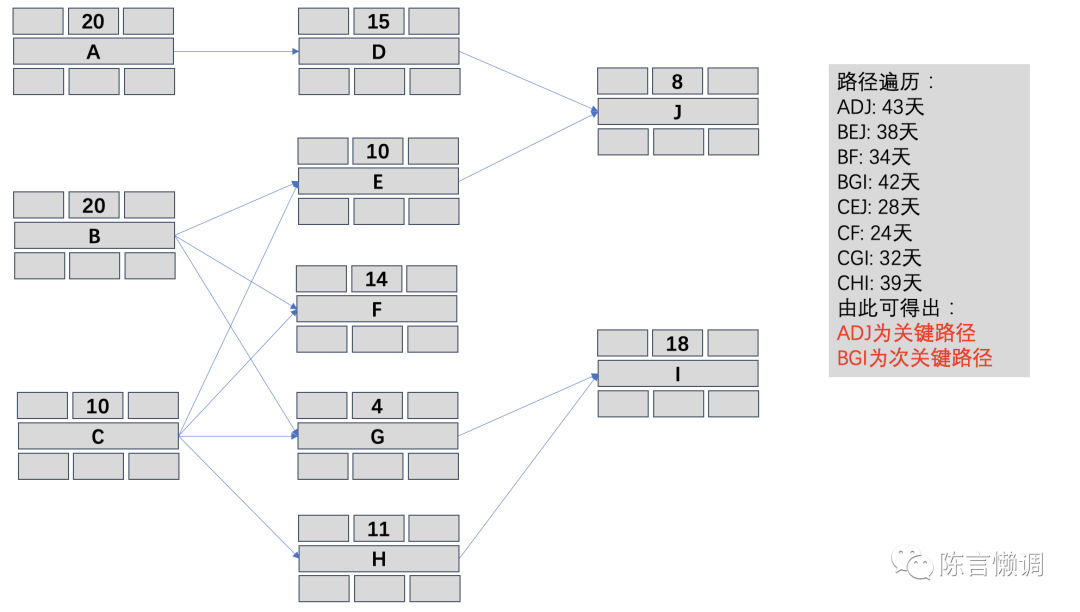
第三步、计算关键路径上的时间
根据关键路径一般都没有浮动时间的特性可以计算出该路径上的所有时间;
解释:最早开始时间为1,最早完成时间=最早开始时间+持续时间-1,因为关键路径没有浮动,所以最晚开始时间、和最晚完成时间与最早一致;得出下图
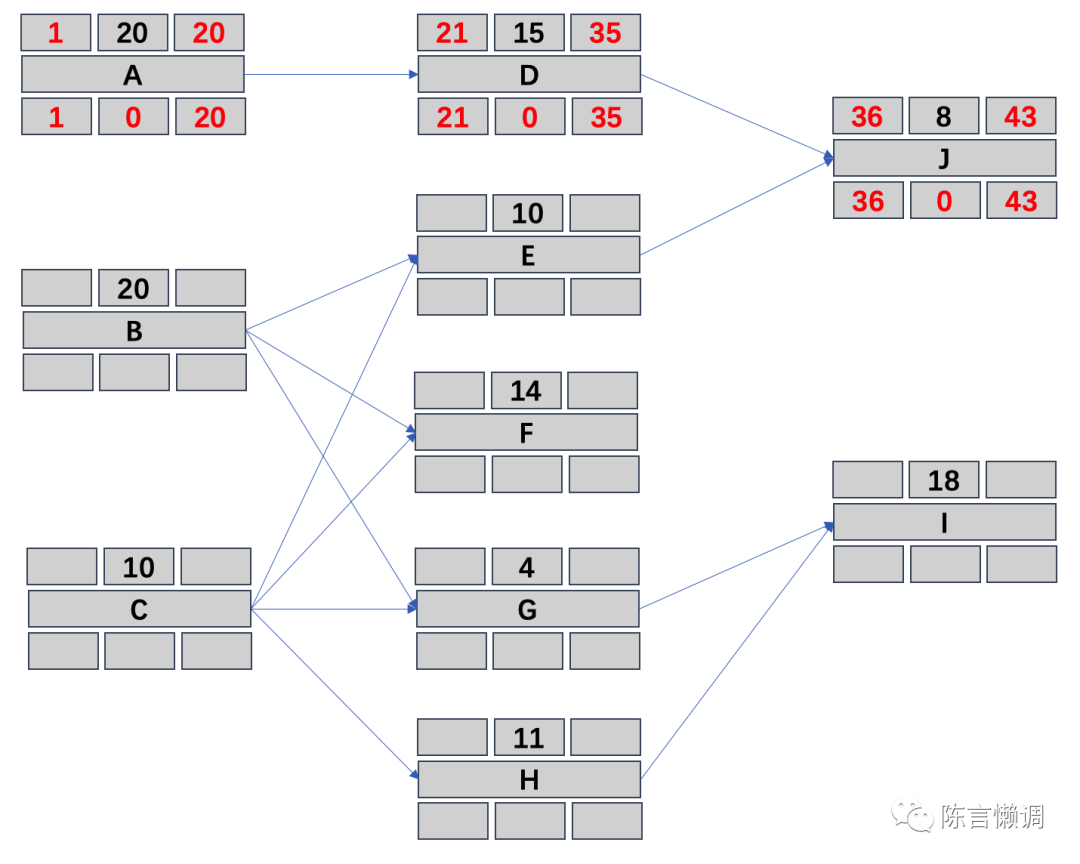
第四步、算出B和C路径上的最早开始时间和最早完成时间
因为B和C也都为开始活动(没有紧前活动),所以可以直接画出B和C路径上的最早开始时间和最早完成时间,此处要注意E、F、G是即跟着B也跟着C的,那么算开始时间的时候要用B和C中完成时间最晚的一个去算,不然就会出现时间冲突,同理I的紧前活动有两个,也要取最晚完成的那个
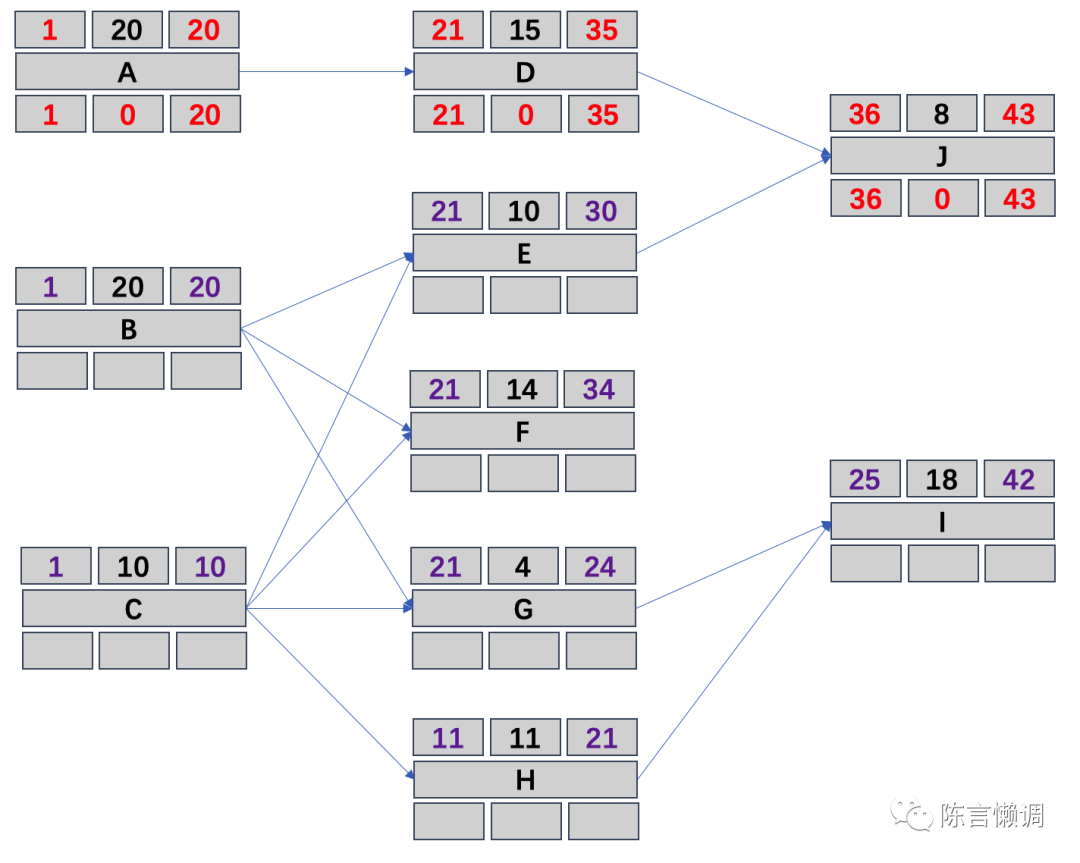
第五步、计算最晚开始时间和最晚完成时间
至此,所有的最早开始时间和最早完成时间都已经计算完成,接下来需要倒推出最晚开始时间和最晚完成时间,因所有路径上的最晚完成时间不能晚于关键路径的最晚完成时间,F、J、I都为结束活动(J为关键已经得出),那么F和I的最晚完成时间不能晚于J,也就可以得出F和I的最晚完成时间为43,那么浮动天数=最晚完成时间-最早完成时间,得出I的浮动时间1,那么最晚开始时间=最早开始时间+浮动天数,得出I的最晚开始时间为26,同理可计算出F的最晚开始时间和最晚完成时间,同时G和H为I的紧前活动,那么计算出G和H的最晚完成时间,根据上诉工时推导出G和H的浮动时间和最晚开始时间,得出下图
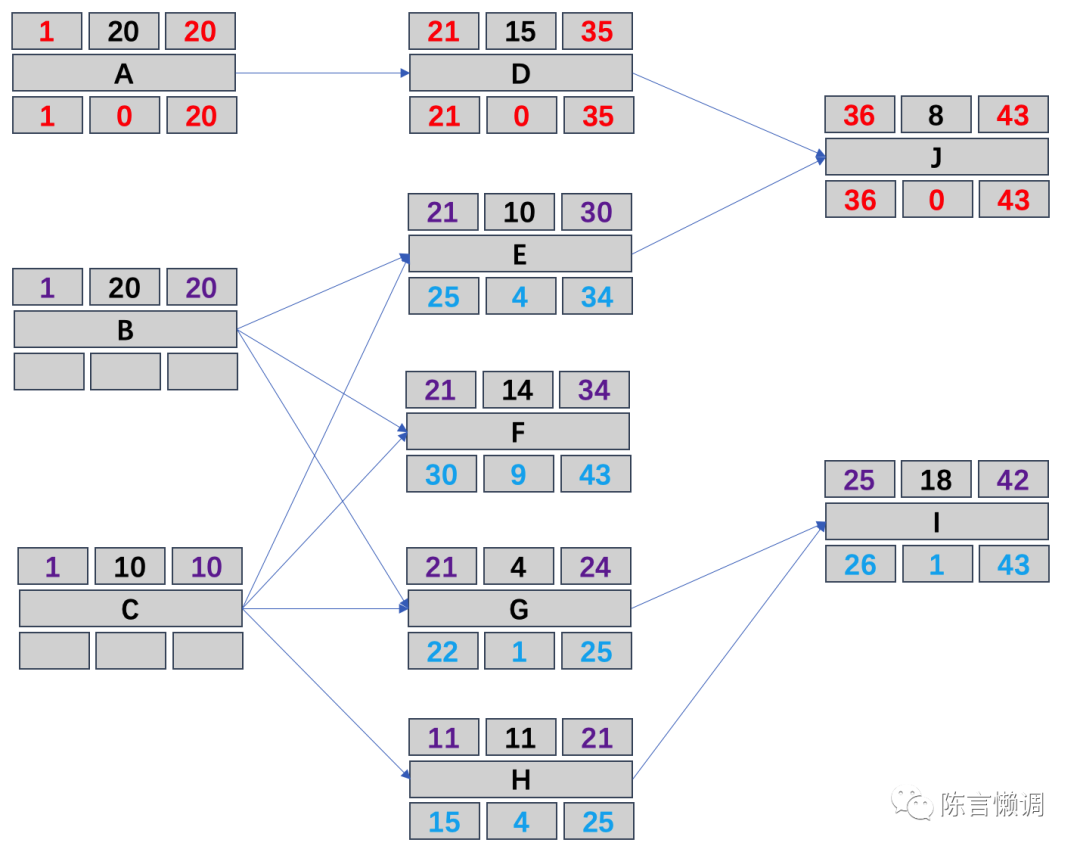
第六步、计算出B和C最晚开始时间和最晚完成时间
B为E、F、G三个活动的紧前活动,C为E、F、G、H四个活动的紧前活动,那么计算B的最晚完成时间要取E、F、G中最晚开始时间最小的那个(否则时间冲突),同理C的计算方式也一样,由此可以计算出B和C的最晚完成时间,根据浮动天数=最晚完成时间-最早完成时间、最晚开始时间=最早开始时间+浮动天数的公式推导出B和C的浮动时间和最晚开始时间。至此,全部计算完成,得出完整图示
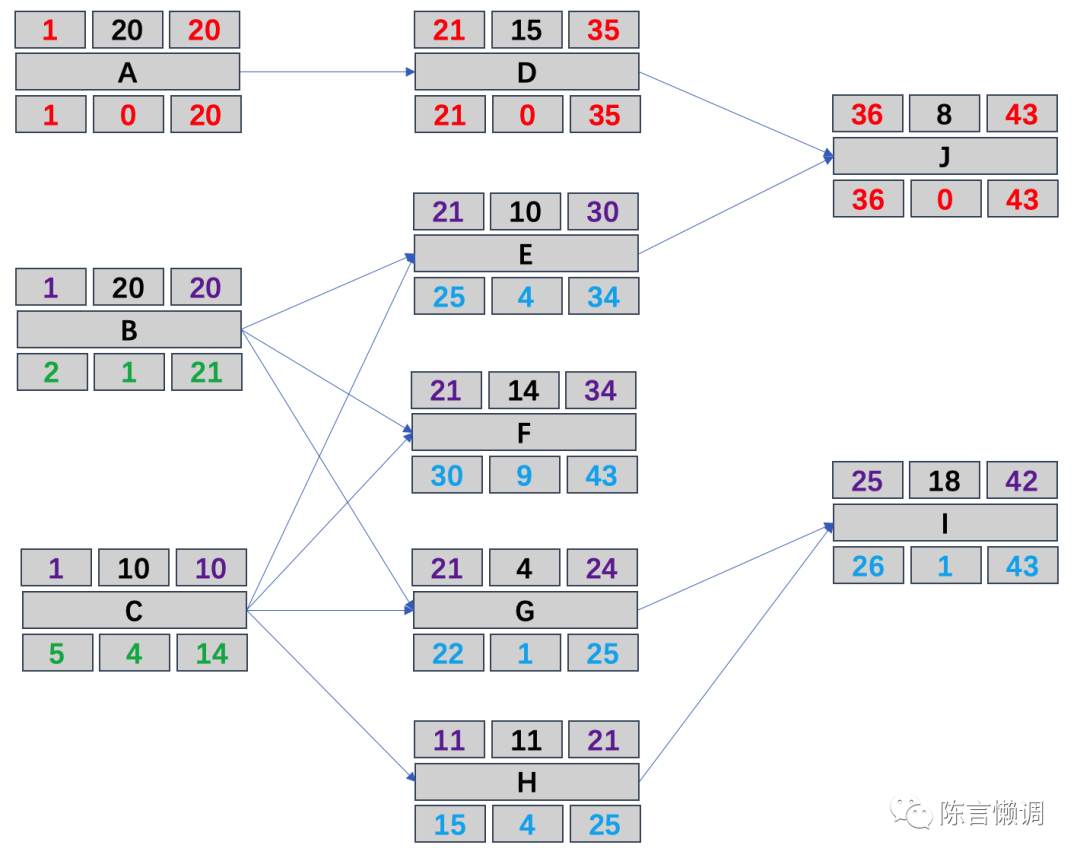
【真题】
1.在下面的活动图中,从A到J的关键路径是(1),I和J之间的活动开始的最早时间是(2)
(24)A、 ABEGJ B、ADFHJ C、ACFGJ D、ADFIJ
(25)A、13 B、23 C. 29 D、40

【答案】BD
【解析】第一小题直接把答案里四个选项套进去计算路径长度,最长的就是关键路径。计算结果ADFHJ=49,所以它是关键路径。
第二小题最早开始时间,是顺推出来。以!之前最长的那边路径的最早完成时间计算出来。列出!之前的所有路径及长度:
A-C-F-H-I:5+4+20+1=30
A-C-F-I:5+4+4=13
A-D-F-1: 10+9+4=23
A-D-F-H-I:10+9+20+1=40
所以}的最早时间是40,即通过最大路径A-D-F-H-I计算出来的。当然这个图看起来似乎是无向图,路径可以不只上面那几个。但从我们做题的角度来讲,D答案40已是最大的数了,找到了这个路径,答案就是它是不会错了。
2.某项目最初的网络图如下,为了压缩进度,项目经理根据实际情况使用了快速跟进的方法:在任务A已经开始一天后开始实施任务C,从而使任务C与任务A并行3天。这种做法将使项目
A、完工日期不变 B、提前4天完成 C、提前3天完成 D、提前2天完成
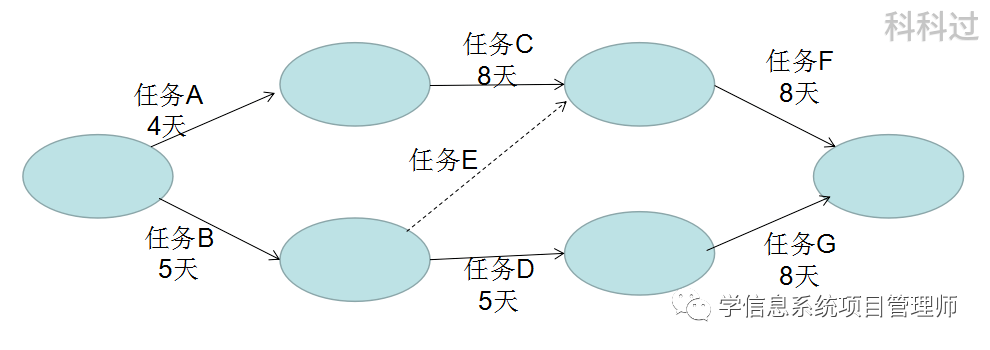
【答案】D
【解析】这题有陷阱。本来关键路径为A-C-F,项目的工期为20天。AC并行3天后,应该是要提前3天完成的,但提前3天后,A-C-F只有17天了,变成不是关键路径了,关键路径变成B-D-G, 18天了,所以相比原20天提前了2天完成。
3.图中,工作E总时差是( )
A、 1 B、2 C、 3 D、4

【答案】D
【解析】直接用关键路径时长减去非关键路径时长。关键路径:ABDF=12E所在的最大路径时长=ACEF=8总时差=12-8=4
4.某项目各项工作的先后顺序及工作时间如下表所示,该项目的总工期为( )天。
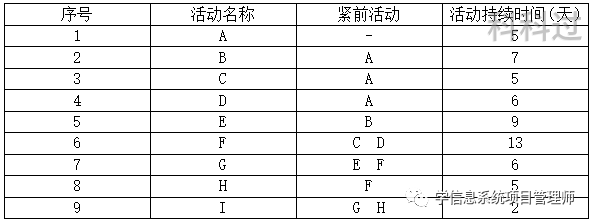
A. 31 B、32 C. 33 D、34
【答案】B
【解析】画图,然后得出关键路径为:A->D一>>F->G->I历时:5+6+13+6+2=32
5.某项目由并行的3个模块A, B和C组成,其中活动A需要3人5天时间完成,活动B需要6人7天时间完成,活动C需要4人2天时间完成,为了保证项目在最短时间内完成,则最少应该为项目配置(1)人。假设活动A, B和C按时完成的概率分别为80%, 70%和100%,则该项目按时完成的概率为(2)
(1)A、 6 B、9 C、 10 、 D、13
(2)A、 50% B、56% C、 64% D、90%
【答案】C, B
【解析】此为较简单的网络图,在7天内完成,人数配置为10人。项目按时完成的概率=80%* 70%* 100%=56%