说明

这篇论文比较短，但是提出的方法确很不错。联邦学习或者分布式机器学习中减少通信开销一般有两种方法：

1. 减少发送的数据量；
2. 通过改变通信的拓扑结构；

本文通过选取重要的梯度进行更新而减少通信的开销，属于第一种方式。
本篇论文是2018年的论文，属于比较新的论文（现在是2023年）。
论文的原文链接：eSGD: Communication Efficient Distributed Deep Learning on the Edge

ABS

在边缘设备上训练越来越流行，但是在边缘设备上进行训练，需要进行参数聚合，而参数聚合需要消耗大量的通信资源。

现在已经有很多方法能够减少通信资源的消耗。而eSGD是另外一种方法，该方法重点根据两个机制实现：

1. 梯度是稀疏的（指梯度中有很多项接近$0$），由这一点得到了不同参数的梯度拥有着不同的重要程度，所以可以只选择某些重要的梯度进行参数的聚合，而不需要选择所有的梯度；
2. 为了防止未被选择的梯度严重严重影响准确性，为没有被选中的梯度提供了残余机制，该机制能够让没有被选中的梯度的更新在本地进行累计，当达到一定值的时候再发送给服务器。

eSGD在MNIST上的效果不戳，即使每次只选择$12.5\%$的梯度进行更新准确度也能达到$81.5$。

1 INTRO

我们将所有的参数依次进行编号，如果有两层，第一层编号为$1,2,3$，那么第二层的参数应该从$4$进行编号。这样我们就可以通过$g_i$来表示第$i$维的梯度。

之前已经有论文发现：大量的参数的值在参与训练后非常接近于$0$（可以理解这一部分的值更新量非常少）。这也就说明了有许多的梯度的值非常接近$0$（只有梯度的值接近$0$才回出现相对应的参数不会有太大的变化，参数才有可能稳定在$0$附近）。而由于每个边缘设备拥有的数据量是非常少的，这就导致会有更多的数据的梯度接近$0$。这些特性使得只选取少量重要的梯度进行参数聚合成为可能。作者设置了一个$H$变量，其中$H_i$用来表示编号为$i$梯度的重要程度，该值是动态更新的，每一轮会根据选择更新的梯度来更新对应的$H$值，这意味着重要的梯度会越来越重要，这也是符合常识的（例如财富会向少数富人聚集）。

除了重要的梯度之外，作者还发现，即使有的梯度非常接近$0$，但是一旦这些梯度参与更新，那么整个模型的准确性会有巨大的变化，所以作者不打算直接舍弃这些小梯度，而是使用了一种方法将这类小的梯度进行累计起来，当达到一定值的时候，在选择参与更新。

2 Related Work

有两类相关工作来减少通信发送的数据量：

Vector Quantization：通过降低梯度的精度，或者使用近似值来代替原有的梯度，从而使得通信所需要传递的数据量减少。

Gradient Sparsification：作者所做的工作属于这一范畴，每次选择一部分重要的梯度进行参与更新。例如之前提出了，固定的threshold只有梯度大于$threshold$的才能进行更新，但是直接这样做似乎$BLEU$分数不理想。

3 eSGD Technique

3.1 Observations

一般的参数聚合使用的方法是：
$$x_t=x_{t-1}-\gamma \frac{1}{Nb}{\Sigma }_i^N{\Sigma }_z\nabla L(x,z)$$
$x_t$代表$t$轮的时候的参数，$\gamma$代表学习率，$N$代表参与的结点个数，$b$代表每个节点训练数据的大小（为了可读性这里假设的是所有结点拥有的数据量相同），$L(x,z)$代表损失函数的参数为$x$，而输入为$z$。上面的式子也就是新的梯度是所有节点的梯度的平均值。

而如果增加$x_{i,t}$用来表示第$i$个参数在第$t$轮的值，在$T$轮之后结束我们可以用下面的式子来代替上面的式子（这里的式子我认为原文中写的有点问题，根据自己的理解写了一下）：
$$x_{i,t}=x_{i,t-1}-\gamma \frac{1}{NbT}{\Sigma }_i^N{\Sigma }_z{\Sigma }_j^{T-1}\nabla L(x_j,z)$$
作者写出这个式子的目的是为了说明，参与更新的梯度可以不立即进行而是将每一轮的梯度进行累计起来再进行更新。（这样似乎是很符合常识的，但是这一部分作者并没有做过多的解释，同时这里的梯度累积应该不能跨越过长的轮数，因为之前有论文做过实验：让每个结点执行到局部最优解的时候在进行更新得到的全局模型效果并不好）

3.2 Importance Updating

有了上面的Observations（即梯度的更新可以累积一定轮数后再进行同步），这一部分作者就讲如何选择重要的梯度。

算法的过程如Algorithm 1所示，这里有一些需要注意的地方：

• $H$的大小是用于做权重随机选择的时候会用上，所谓权重随机选择是指$H$越大的值被选中的概率越大；
• $t=0或1$的时候，是直接进行随机选择；

上面的Algorithm 1每一轮选择参与更新的梯度个数是总梯度的个数的$k\%$，其基本的思想是通过比较当前更新后的损失$l(x_t)$和上一轮的损失$l(x_{t-1})$，如果当前的损失较小，那么此时我们可以认为上一轮选择进行更新的梯度是合理的，那么此时我们依然选择上一轮进行更新的梯度进行更新，同时我们会更新被选中的梯度的$H$值，这也意味着随着算法的进行，重要的梯度可能会变得越来越重要，从而被选取的几率会越来越大。如果当前的损失反而比上一轮的损失大，那么我们此时进行权重随机选取$k\%$的梯度进行更新。

3.3 Momentum Residual Accumulation

上述判断完成之后我们会进行未选中的梯度累加，当未选中的梯度的累计值达到阈值之后，未选中的梯度会替代掉本轮选择的部分梯度，替换方法如下：首先将预先选择的梯度的$H$值进行从大到小排序，每一次的替换会选择$H$最小的梯度进行替换。

下面来看如何进行未选中的梯度累加：

上述算法中设置$\beta$的目的是为了防止梯度过时，因为之前提到过可能当间隔的久了，这些梯度参与更新的效果可能并不那么好，于是设置了$\beta$参数，每次进行累计的时候，上一轮的值只选取$\beta$的部分。

阈值的设定：从算法一的开头可以看到阈值为所有梯度的均值这说明阈值是动态变化的，这样设置的好处是能够尽可能的让所有的梯度都能或早或晚的参与更新。如果不使用动态变化的阈值，而是将其固定为某一个值，那么可能很多比较小的梯度都不会参与更新，使用平均值能够让其中一部分更有可能的参与更新。

4 Experiment

4.1 Experiment Settings

数据集：MNIST data set

测试平台：MATLAB 2018R

超参数的设定：$\beta =0.9,\gamma =\frac{0.1}{2e}$,$e$代表的是epoch

分别做了不同丢弃率的实验（根据$Algorithm1$的$k$参数不同进行实验）。

Figure 2展示的是不同$k$下的损失随着迭代次数的变化：

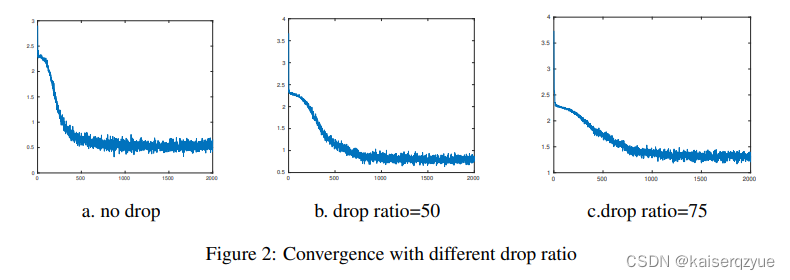
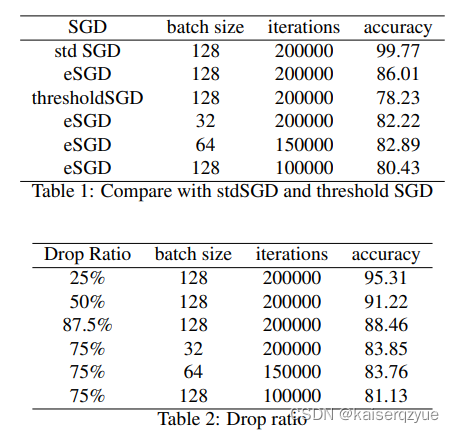
Table 1和Table 2给出了不同方法的和不同超参数下的准确率。其中std SGD表示标准$SGD$（也就是每次选择所有的梯度进行更新），$thresholdSGD$指的是选取梯度大于固定的阈值的梯度进行更新。

5 Conclusions

实验的结果表明，即使丢弃掉接近$90\%$的梯度（这意味着在通信条件不变的情况下，通信的开销变为原来的$\frac{1}{10}$），准确率也能非常高（从$99\%$降到了$88\%$，下降的比例非常低）。