文章目录
- 什么是线性规划(Linear Programming,LP)?
- 线性规划的标准形式
- 非标准形LP模型转化为标准形LP模型
- 基本概念
- 基本解&基矩阵&基变量&非基变量
- 基本可行解&可行基矩阵&非退化的基本可行解&退化的基本可行解
- 基本可行解存在性
- 求基本可行解
- 示例:求基本可行解
- 求最优解
- 方法一(暴力枚举):求出所有基本可行解找最小
- 方法二(迭代):从一个基本可行解跳转到一个目标函数值更小的基本可行解
- 多面体
- 多面体基本性质
- 多面体的极点
- 示例:求极点
- 多面体S有多少个极点?- 有限个 & 最多 C n m C_n^m Cnm
- 多面体的方向
- 多面体的极方向
- 多面体的极方向有多少个?- 有限个
- 示例:求极方向
- 多面体分解定理
- 多面体分解定理有什么作用?
- 单纯形法
- 基本思想
- 原理
- 方法
- 1 确定出基变量和出基向量的下标
- 2 确定进基变量和进基向量的下标
- 3 确定进基变量的值
- 终止条件
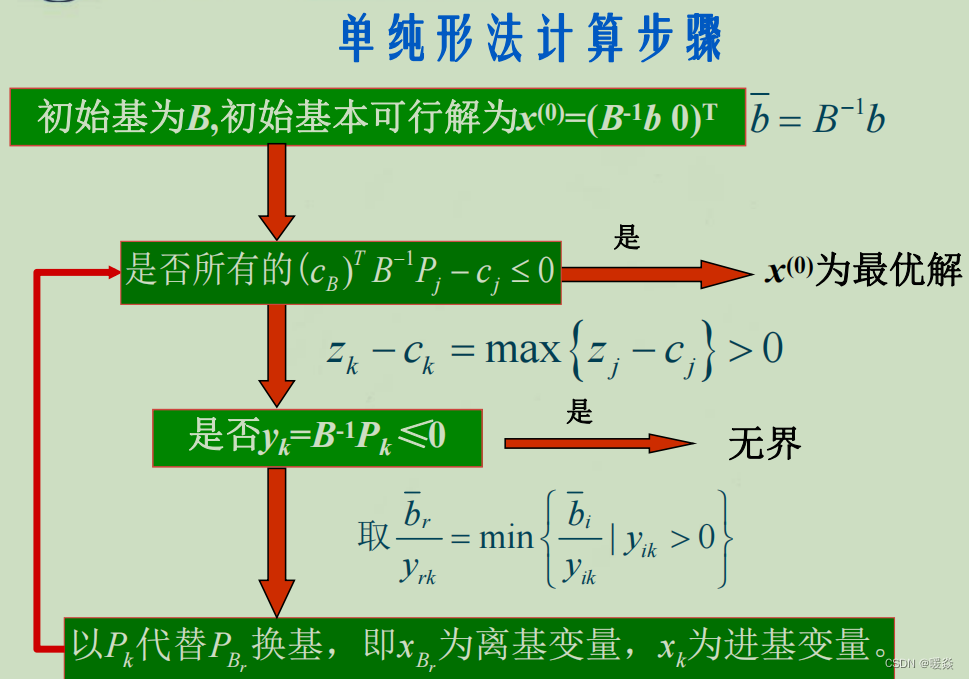
- 单纯形法计算步骤
- 单纯形法表格形式
什么是线性规划(Linear Programming,LP)?
目标函数为决策变量的线性函数,同时约束条件为线性等式或线性不等式约束。
线性规划的标准形式

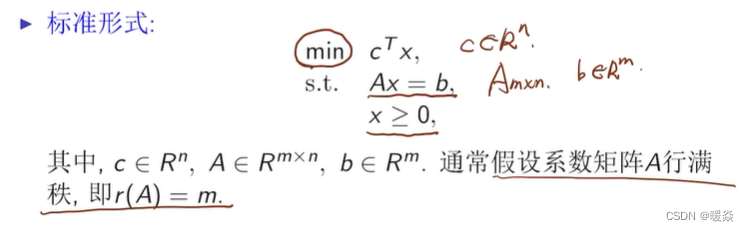
非标准形LP模型转化为标准形LP模型

基本概念

基本解&基矩阵&基变量&非基变量
基本可行解&可行基矩阵&非退化的基本可行解&退化的基本可行解

基本可行解存在性

求基本可行解
求基本可行解<=>求极点<=>求可行基矩阵<=>
A
m
∗
n
A_{m*n}
Am∗n矩阵m个线性无关列

示例:求基本可行解

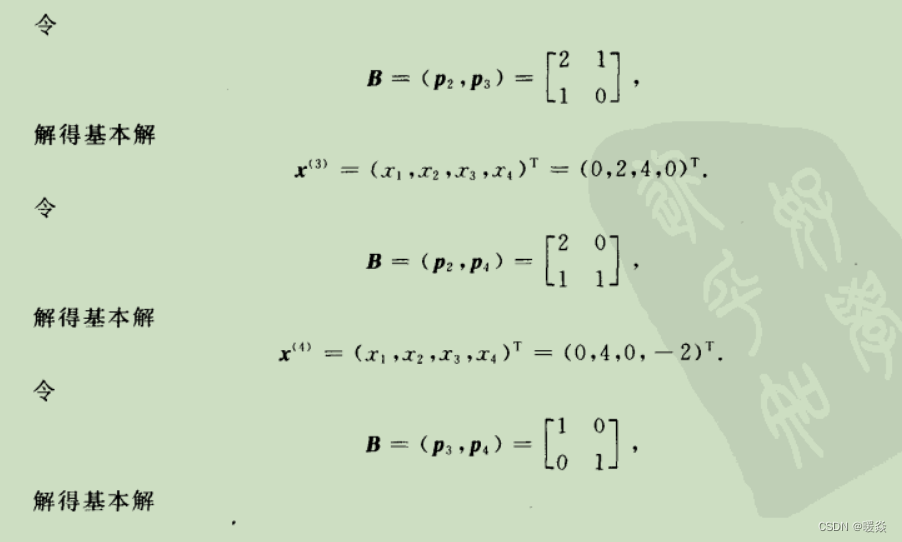

求最优解
方法一(暴力枚举):求出所有基本可行解找最小
求出所有基本可行解(即求极点)。
代入目标函数找出最小极点(该最小极点即为最优解,因为最优解一定在极点取得)。
方法二(迭代):从一个基本可行解跳转到一个目标函数值更小的基本可行解

多面体
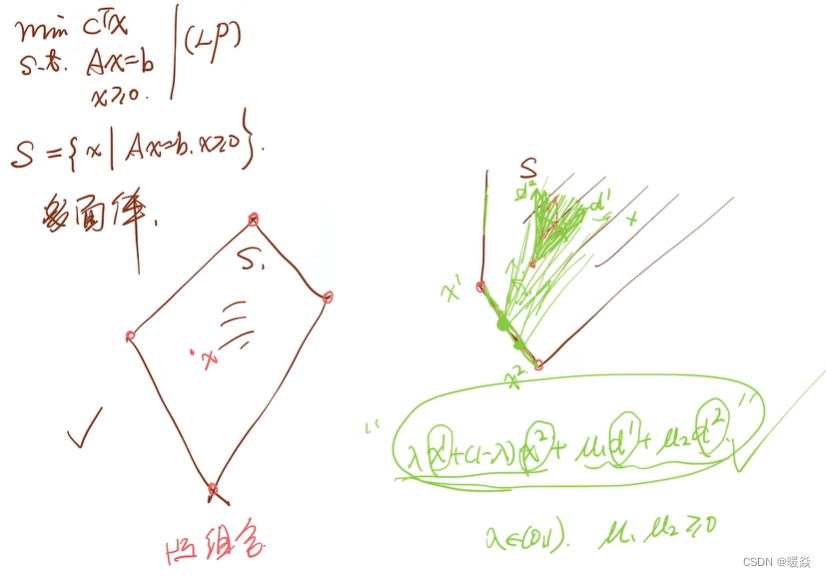
多面体基本性质

多面体的极点



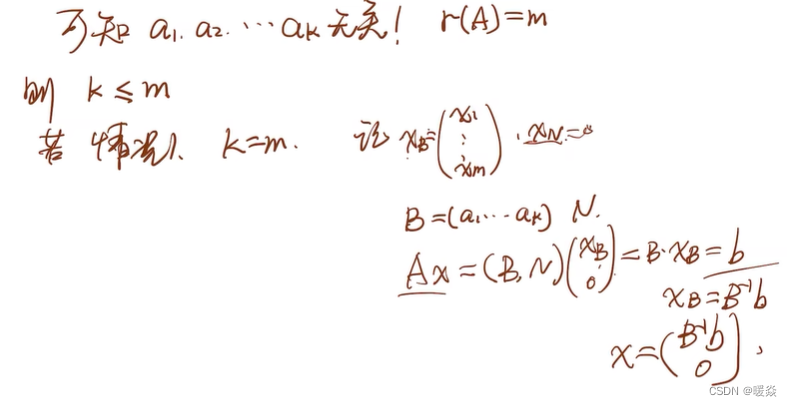

x若是极点,正分量对应的A的列一定线性无关。
示例:求极点
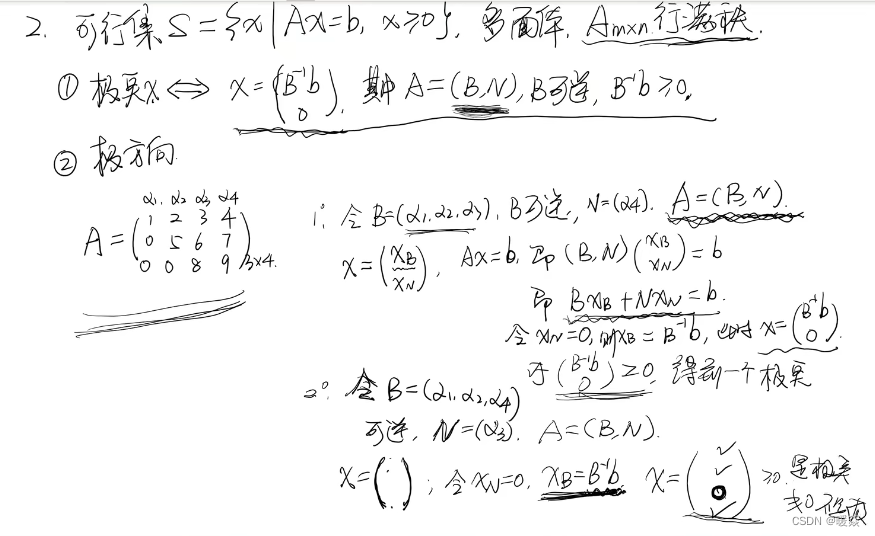
多面体S有多少个极点?- 有限个 & 最多 C n m C_n^m Cnm
最多有
C
n
m
C_n^m
Cnm个极点,一般都少于
C
n
m
C_n^m
Cnm,有两个原因。
原因1:从n个列中选出m列不一定线性无关。
原因2:即使这m列线性无关,其组成的B也不一定满足
B
−
1
b
≥
0
B^{-1}b\ge 0
B−1b≥0。
多面体的方向
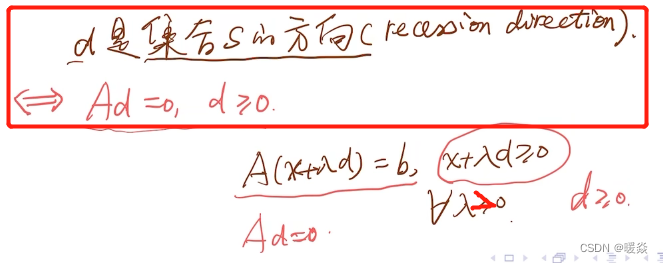
多面体的极方向


多面体的极方向有多少个?- 有限个


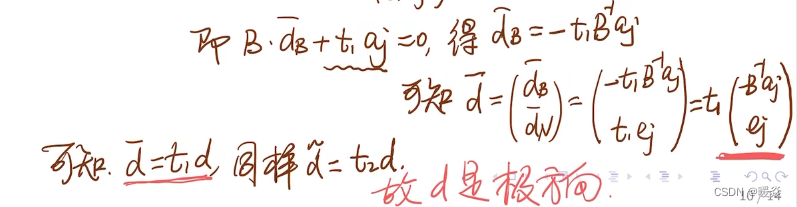



示例:求极方向

d≥0
多面体分解定理
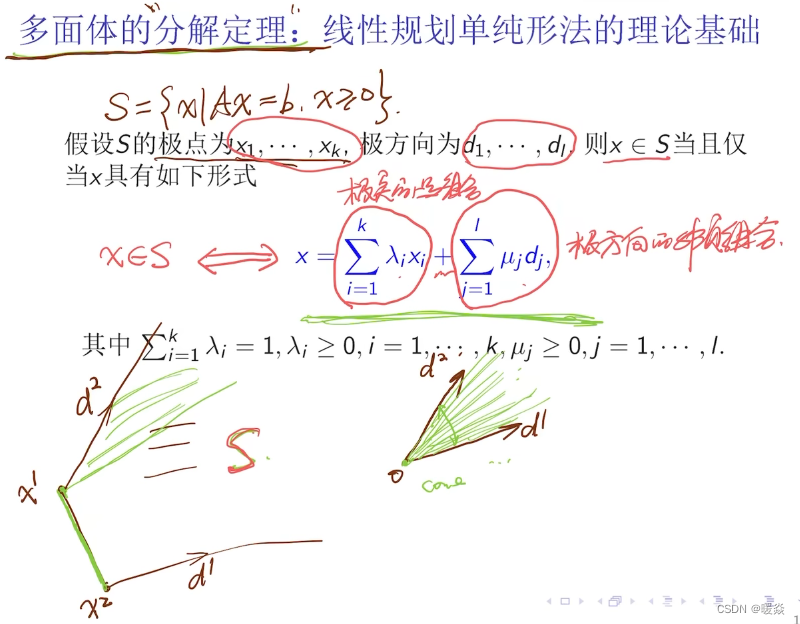
多面体分解定理有什么作用?


重新表示可行集
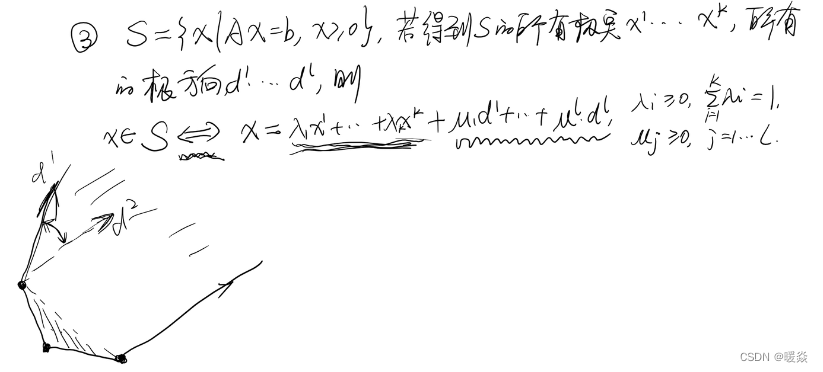
重新定义线性规划问题
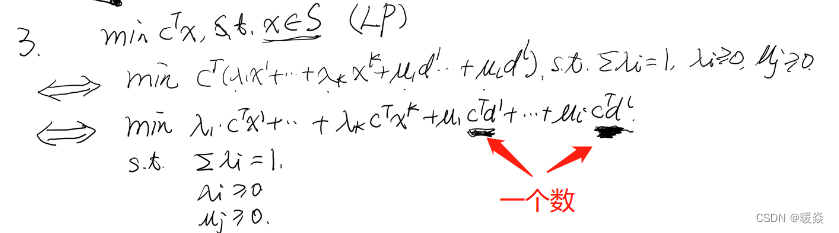

为什么 min ∑ λ i C T x i \min \sum \lambda_i C^Tx_i min∑λiCTxi等价于 min C T x i , i = 1 , . . . , k \min C^Tx_i,i=1,...,k minCTxi,i=1,...,k?
求 min C T x i , i = 1 , . . . , k \min C^Tx_i,i=1,...,k minCTxi,i=1,...,k,找到最小 x r x_r xr就是最优值点,令 min ∑ λ i C T x i \min \sum \lambda_i C^Tx_i min∑λiCTxi中 λ r = 1 \lambda_r=1 λr=1其他的λ都为0, C T x r C^Tx_r CTxr就是最优值。
何时有最优解?
C T d j ≥ 0 C^Td_j \ge 0 CTdj≥0时,存在最优解。
C T d j < 0 C^Td_j \lt 0 CTdj<0时,无解。
最优解是什么?
最优解一定在极点上取到。
min C T x i , i = 1 , . . . , k \min C^Tx_i,i=1,...,k minCTxi,i=1,...,k,找到最小 x r x_r xr就是最优值点, C T x r C^Tx_r CTxr就是最优值。
单纯形法

基本思想

原理
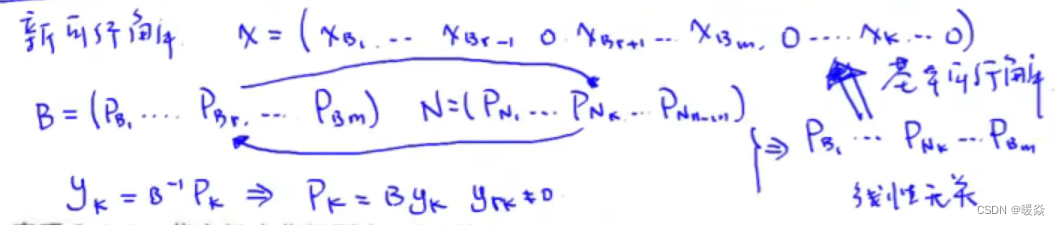
实现基本可行基的转化
方法
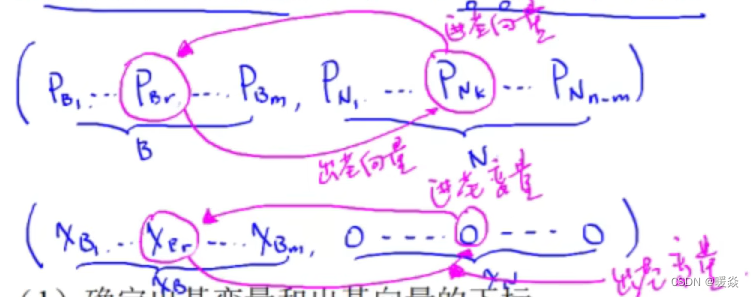
从初始基本可行解出发,求一个改进的基本可行解。
1 确定出基变量和出基向量的下标
2 确定进基变量和进基向量的下标
3 确定进基变量的值
目标函数值只与非基变量有关。
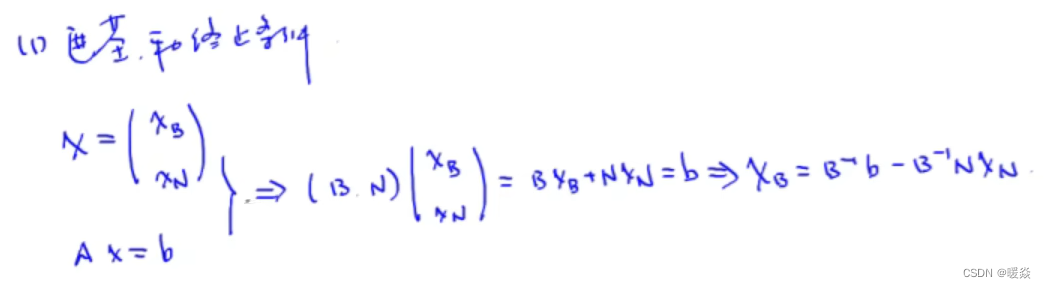




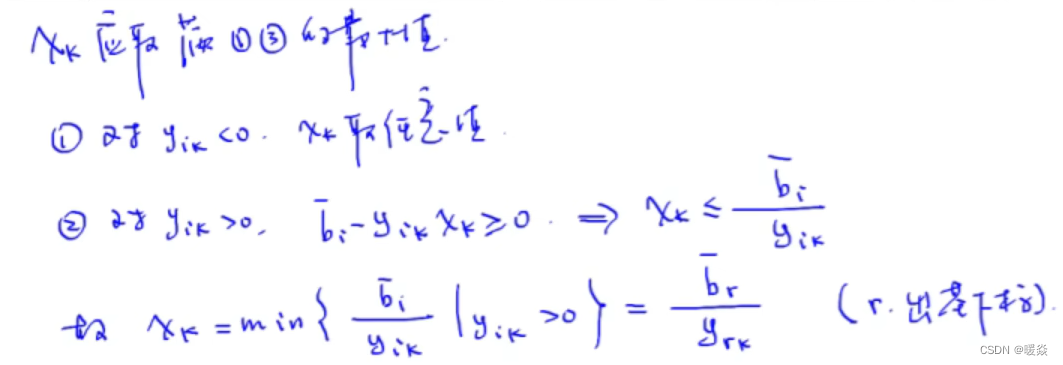
终止条件

单纯形法计算步骤