一、二叉树的前序遍历

题目链接

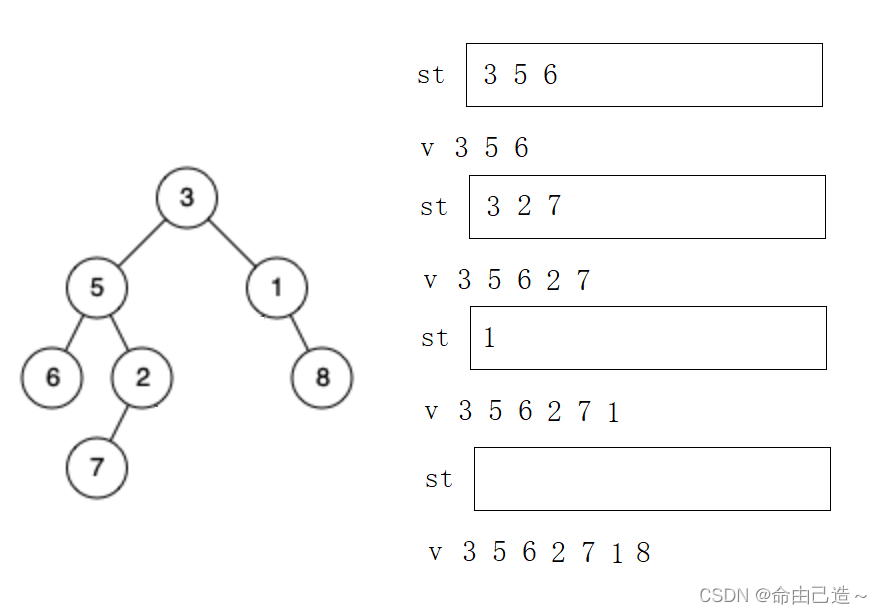
我们可以把任何一棵树看成左路节点，左路节点和右子树。先访问左路节点，再访问左路节点的右子树。在右子树中也重复这种循环，就是非递归遍历二叉树的思想。

解释：
栈st存放节点，v存放数值，cur初始化为root。
循环条件是栈不为空或者cur不为空(访问最后一个节点之前栈就已经为空了)，循环遍历左子树并且把左子树入栈，同时把值存入v中。然后弹出栈顶元素，并且把栈顶元素的右子树赋值给cur，这样就形成了遍历。
当栈不为空的时候说明还有左路节点的右子树没有被访问，当cur不为空的时候说明还有树要被访问。当同时为空的时候才是访问完成。当一个节点出栈的时候说明此时该节点及该节点的左子树已经被访问完成了。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                v.push_back(cur->val);
                cur = cur->left;
            }
            TreeNode* node = st.top();
            st.pop();
            cur = node->right;// 转化成子问题访问右子树
        }
        return v;
    }
};

二、二叉树的中序遍历

题目链接

因为中序遍历的访问顺序是左根右，跟前序遍历不同，所以我们让左节点入栈的时候先不访问，出栈（说明左子树访问完了）时在访问节点。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(!st.empty() || cur)
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* node = st.top();
            st.pop();
            v.push_back(node->val);
            cur = node->right;
        }
        return v;
    }
};

三、二叉树的后序遍历

3.1 方法一

首先我们知道后序遍历就是左右根，而我们可以把访问顺序变成根右左，然后再逆置顺序。而根右左就跟前序遍历的方法一样：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                v.push_back(cur->val);
                cur = cur->right;
            }
            TreeNode* node = st.top();
            st.pop();
            cur = node->left;
        }
        reverse(v.begin(), v.end());
        return v;
    }
};

3.2 方法二

按照常规的遍历方法走左右根，但是这里有一个问题：
当访问到根的时候有两种情况：
1️⃣ 从左子树回来，现在要先访问右子树
2️⃣ 从右子树回来，左右子树已经访问完毕，再访问根。
针对这种情况我们可以在加一个变量来确定是第几次访问根，如果是第一次就访问右子树，如果是第二次就访问。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<pair<TreeNode*, bool>> st;
        vector<int> v;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(make_pair(cur, false));
                cur = cur->left;
            }
            TreeNode* node = st.top().first;
            if(st.top().second == true)
            {
                st.pop();
                v.push_back(node->val);
            }
            else
            {
                st.top().second = true;
                cur = node->right;
            }
        }
        return v;
    }
};