一、二分法引入-猜数游戏

• 二分法:折半搜索。

• 二分的效率:很高，O(logn)

• 例如猜数游戏，若n=1000万，只需要猜log10 7= 24次

• 猜数游戏的代码：

• bin_search------>二分搜索

• 把一个长度为n的有序序列上O(n)的查找时间，优化到了O(logn)。

二、理论背景-非线性方程的求根问题

• 满足方程: f(x)=0的数x称为方程的根。

• 非线性方程:指f(x)中含有三角函数、指数函数或其他超越函数。

• 非线性方程，很难或者无法求得精确解。

• 二分法是一种求解的方法。

三、非线性方程的近似解

• 非线性方程：

在实际应用中，只要得到满足一定精度要求的近似解就可以了。

• 根的存在性：

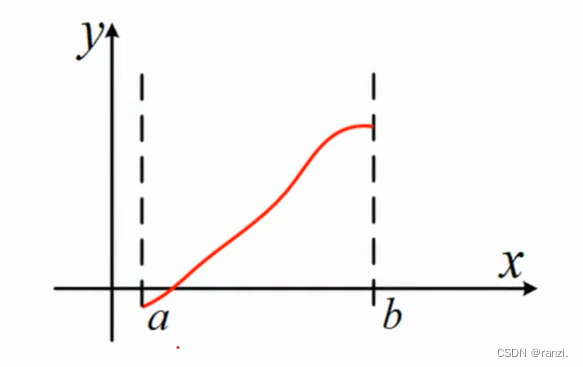
判定:设函数在闭区间[a, b]上连续，且f(a)· f(b) < 0,则f(x)=0存在根。

• 求根：

有两种方法:搜索法、二分法。

• 搜索法

• 二分法

四、使用二分法的两个条件

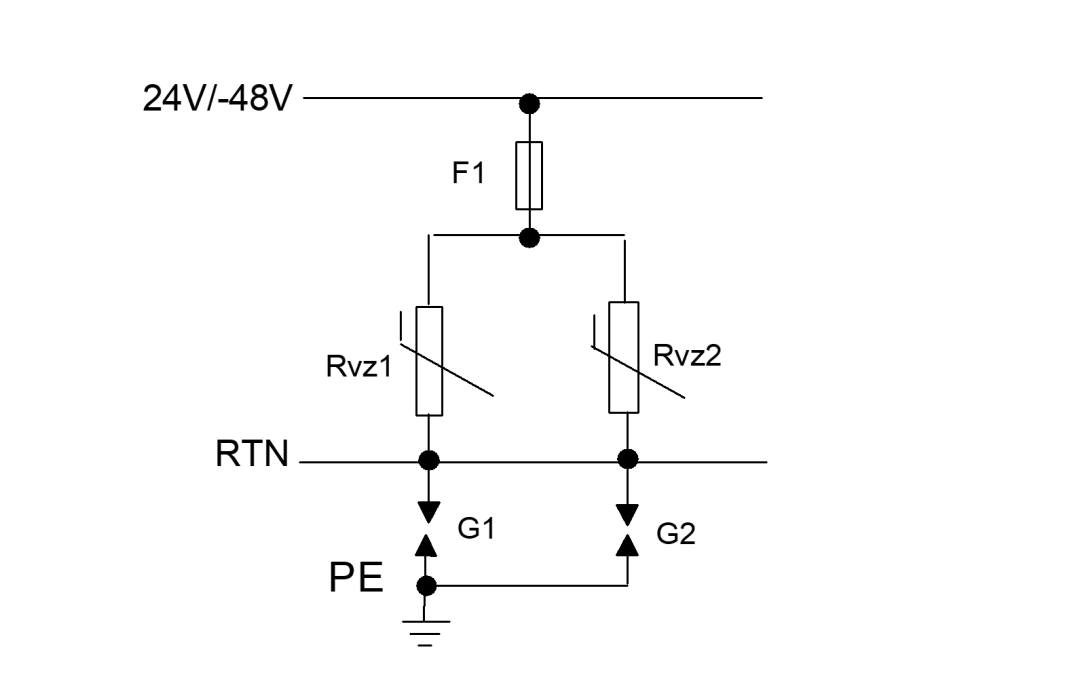
• 上下界[a, b]确定。

• 函数在[a,b]内单调。

五、二分法复杂度

六、整数二分

七、例题

1.例一

在单调递增序列中找X或者X的后继。

在单调递增数列a[]中查找某个数x，如果数列中没有x，找比它大的下一个数。

• a[mid]>=x时:x在mid的左边，新的搜索区间是左半部分，left不变，更新right = mid。

• a[mid]<x时:x在mid的右边，新的搜索区间是半部分，right不变，更新left = mid +1。

• 代码执行完毕后，left = right，两者相等，即答案所处的位置。

2.例二

在单调递增序列中查找X或者X的前驱。

在单调递增数列a[]中查找某个数x，如果数列中没有x，找比它小的前一个数。

• a[mid]<=x时，x在mid的右边，新的搜索区间是右半部分，所以right不变，更新left =mid。

• a[mid]>x时，x在mid的左边，新的搜索区间是左半部分，所以left不变，更新right = mid -1

3.对比

八、真题实例1

1.真题解析

2.输入部分的代码

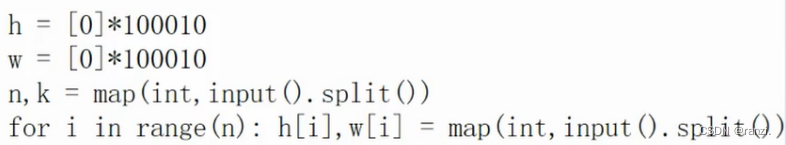
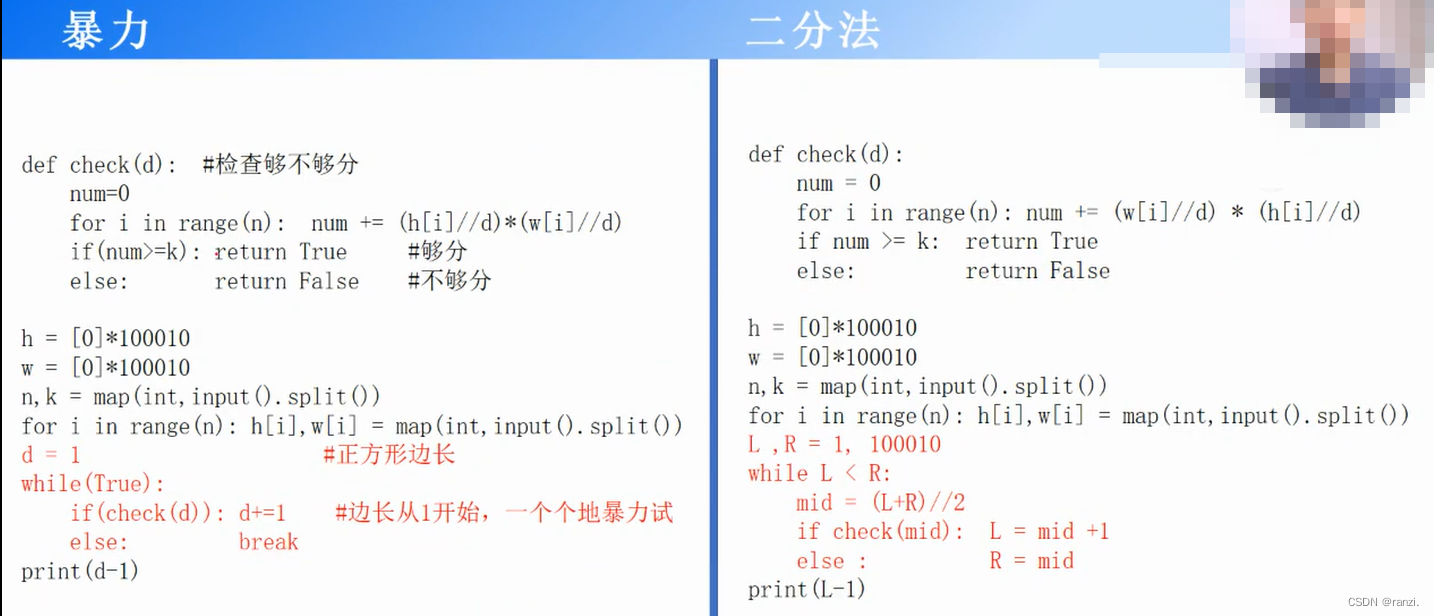
3.暴力法解题

把边长从1开始到最大边长d，每个值都试一遍，一直试到刚好够分的最大边长为止。

编码:边长初始值d=1，然后d=2,3,4,...一个个试。

4.暴力法复杂度

复杂度:n个长方形，长方形的最大边长d。

check()计算量是O(n)，做d次check()，总复杂度O(nxd)，n和d的最大值是10的5次方，超时。

---

5.二分法解题

一个个试边长d太慢，用二分法，按前面的“猜数游戏”的方法猜d的取值。

暴力法需要做d次check(),用二分法，只需要做O(logd)次check()，总复杂度O(nlogd)。

---

6.两种方法对比

九、真题实例2

1.二分法套路题：最小值最大化、最大值最小化

在n块岩石中移走m个石头，有很多种移动方法

在第i种移动方法中，剩下的石头之间的距离，有一个最小距离ai。

在所有移动方法的最小距离ai中，问最大的ai是多少。

在所有可能的最小值中，找最大的那个，就是“最小值最大化”。

2.暴力法解题

找所有的组合，在n块岩石中选m个石头的组合。情况太多，超时。

3.二分法解题

不找搬走石头的各种组合，而是给出一个距离d，检查能不能搬走m块石头而得到最短距离d。把所有的d都试一遍，肯定能找到一个最短的d。用二分法找这个d。

4.输入部分的代码

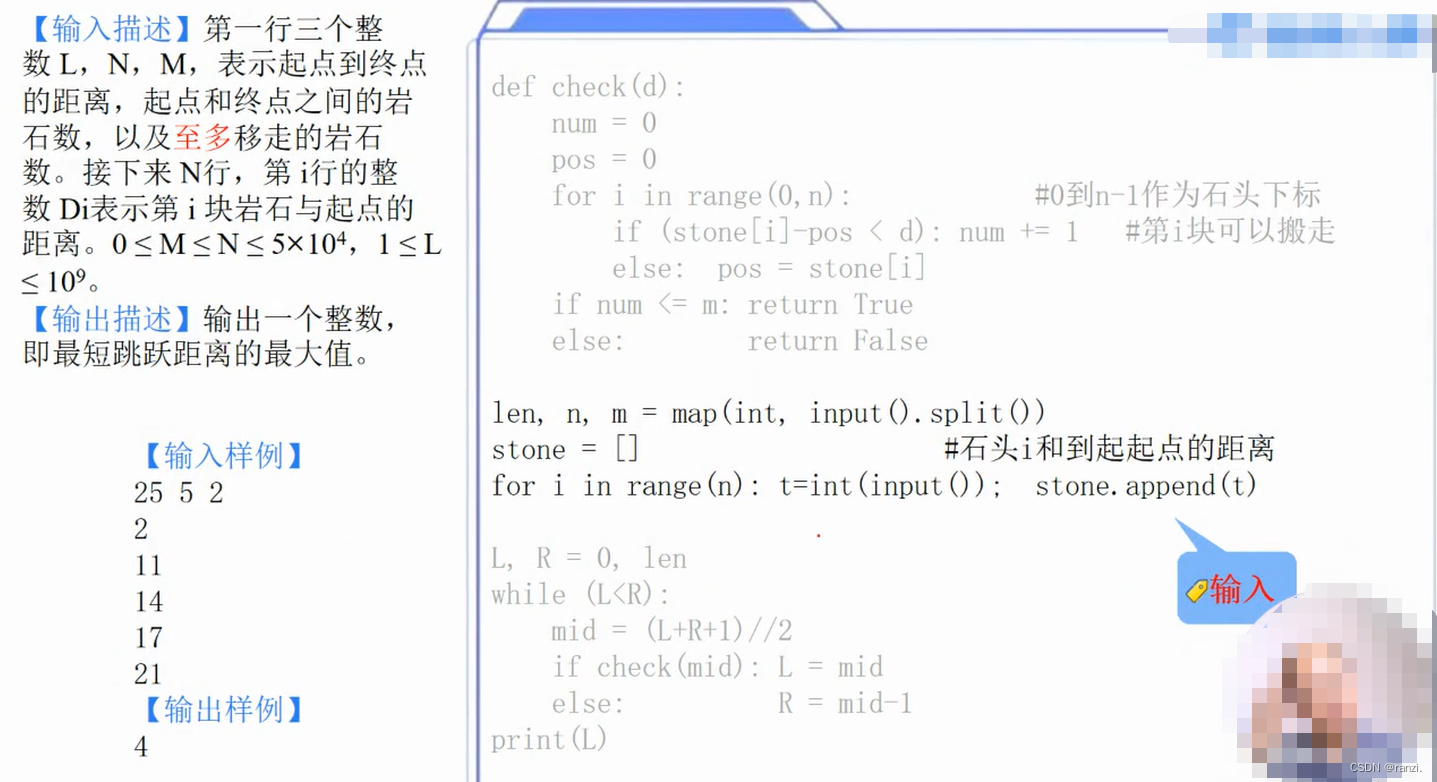
5.检查距离d是否合适:贪心法

6.用二分法找最小距离d

十、实数二分

• 与整数二分法相比，实数二分容易多了，不用考虑整数的取整问题。

• 两种写法: while、for。

十一、真实例题3

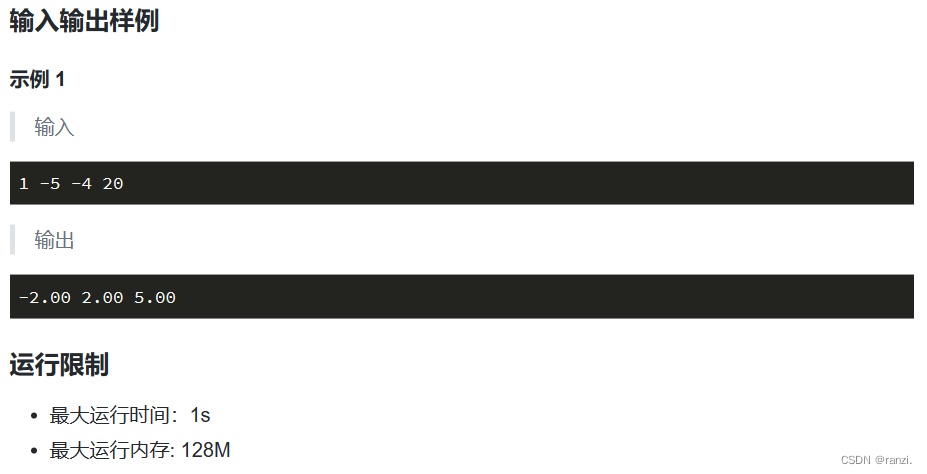
1.暴力法解题

本题数据范围小，可以用暴力法模拟。

一元三次方程有3个解，用暴力法，在根的范围[-100,100]内一个个试。答案只要求3个精度为2位小数的实数，那么只需要试200*100=20000次就行了。判断一个数是解的方法:如果函数值是连续变化的，且函数值在解的两边分别是大于0和小于0，那么解就在它们中间。例如函数值f(i)和f(j)分别大于、小于0，那么解就在[i,j]内。

2.二分法解题

如果题目要“精确到小数点后6位”，上面的暴力法需要计算200*106次，超时了。

二分法:题目给了一个很好的条件:根与根之差的绝对值大于等于1。在每个[i,i+1]小区间内做二分查找。

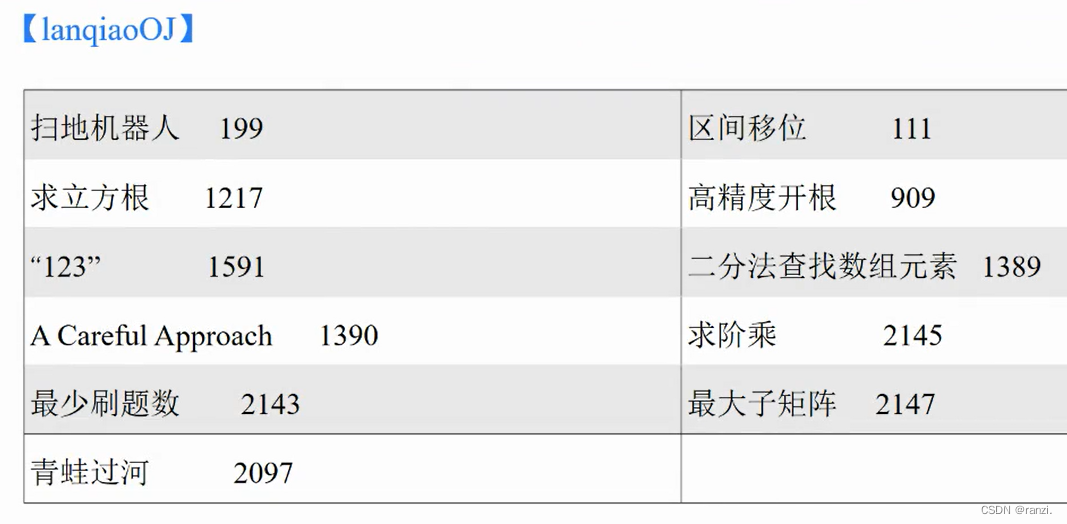
十二、二分法练习习题