面试浅谈之十大排序算法

HELLO，各位博友好，我是阿呆 🙈🙈🙈

这里是面试浅谈系列，收录在专栏面试中 😜😜😜

本系列将记录一些阿呆个人整理的面试题 🏃🏃🏃

OK，兄弟们，废话不多直接开冲 🌞🌞🌞

一 🏠 概述

排序定义

对一序列对象根据某个关键字进行排序

术语

• 稳定：如果 a 在 b 前，且 a = b，排序后 a 仍在 b 前
• 不稳定：如果 a 在 b 前，且 a = b，排序后 a 可能在 b 后
• 内排序：所有排序操作在内存中完成
• 外排序：数据太大，因此放在磁盘中，排序通过磁盘和内存数据传输进行
• 时间复杂度： 算法执行所耗费时间
• 空间复杂度：算法执行所耗费内存

算法总结

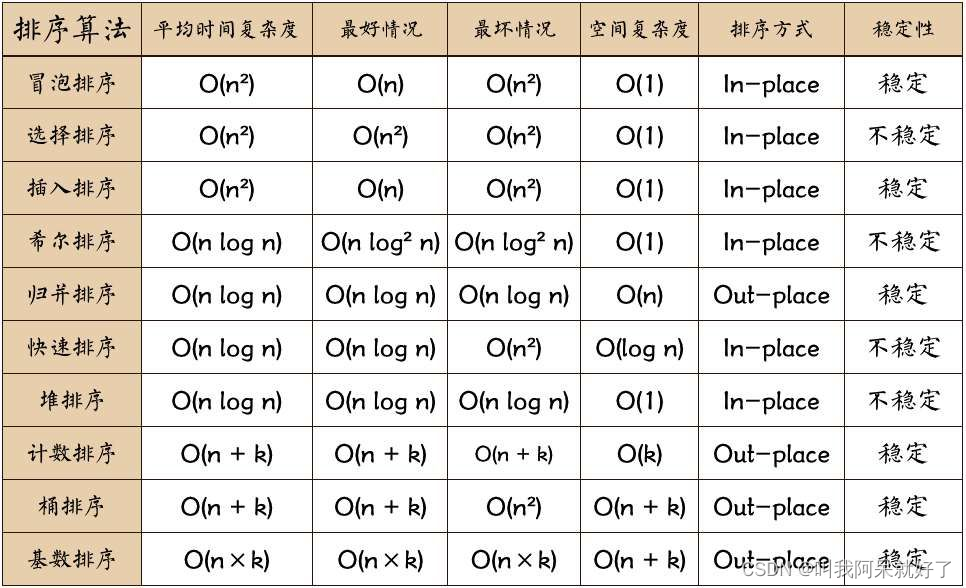
名词解释

• n : 数据规模
• k : 桶个数
• In-place : 占用常数内存，不占用额外内存
• Out-place : 占用额外内存

算法分类

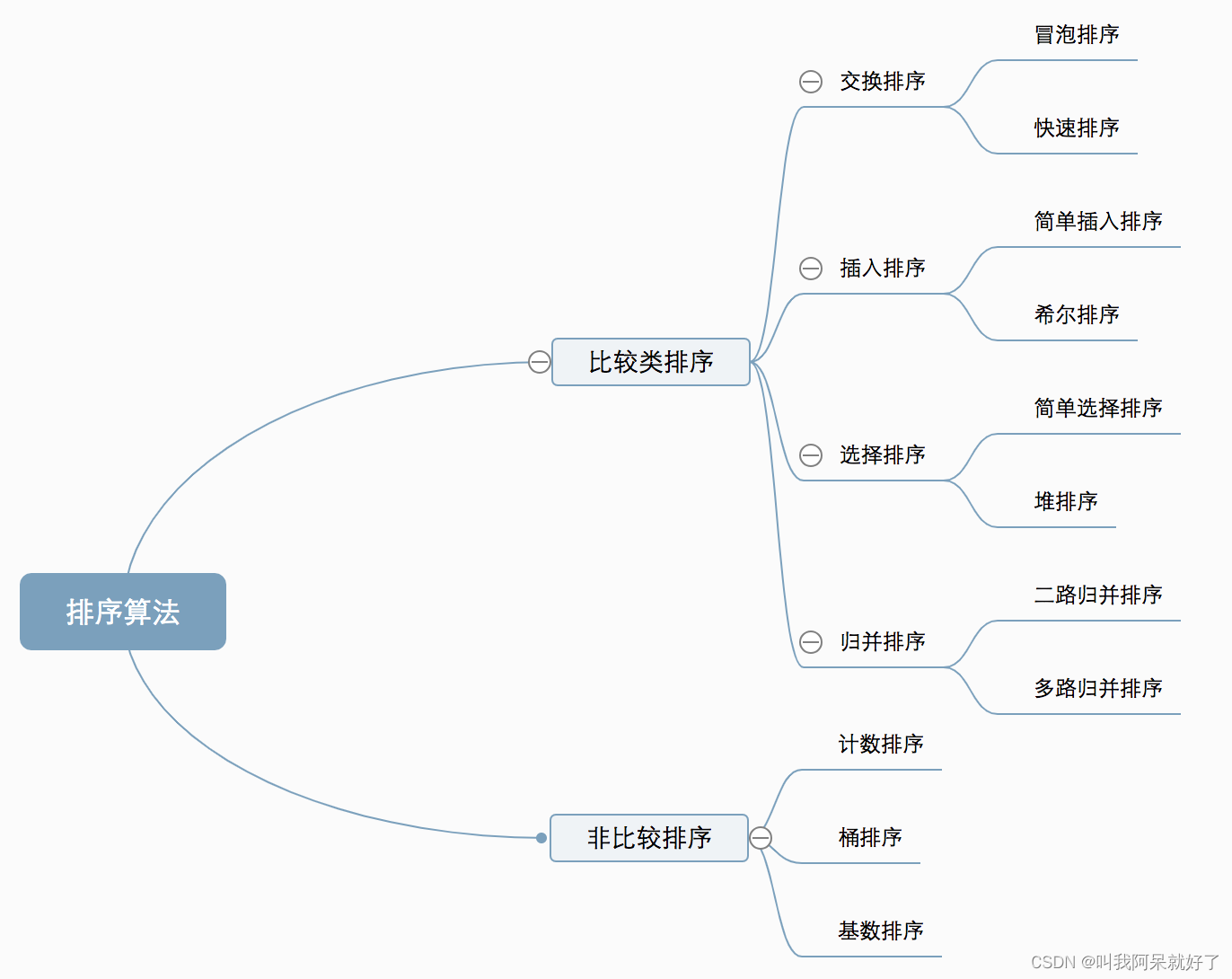
比较和非比较区别

常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里，元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较，才能确定自己的位置

在冒泡排序之类的排序中，问题规模为 n，又因为需要比较n次，所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中，问题规模通过分治法消减为logN次，所以时间复杂度平均O(nlogn)

比较排序的优势是，适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况

计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。针对数组arr，计算arr[i]之前有多少个元素，则唯一确定了arr[i]在排序后数组中的位置。非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。算法时间复杂度O(n)

非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求

二 🏠 核心

冒泡排序（Bubble Sort）

冒泡排序，重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来

算法描述

• 比较相邻的元素，如果第一个比第二个大，就交换它们两个
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数
• 针对所有的元素重复以上的步骤，除了最后一个
• 重复步骤1~3，直到排序完成

代码实现

// 两数交换
void mySwap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}

// 冒泡排序
void BubbleSort(vector<int> &num) {
    bool sortFlag; //某趟排序后已有序, 则不需要再空跑趟
    int len = num.size();
    for (int i = 0; i < len; ++i) {
        for (int j = 0; j < len - i - 1; ++j) {
            if (num[j + 1] < num[j])
                mySwap(num[j + 1], num[j]);
        }
        if (!sortFlag) return vec;
    }
}

选择排序（Selection Sort）

首先找到数组最小元素，将它和数组第一个元素交换位置。在剩下元素中找到最小元素，将它与数组第二个元素交换位置，如此往复，直至 n - 1 结束

算法描述

• 初始状态 ：无序区为 R[1…n]，有序区为空
• 第 i 趟排序 (i = 1, 2, 3 … n - 1) 开始时，当前有序区和无序区分别为R [1 … i - 1] 和 R (i … n）。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第 1 个记录 R 交换，使 R[1 … i] 和 R[i+1 … n) 分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
• n - 1 趟结束，数组有序化了

代码实现

// 选择排序
void SelectionSort(vector<int> &num) {
	int len = num.size();
    for (int i = 0; i < len - 1; ++i) {
        int minPos = i;
        for (int j = i + 1; j < len; ++j) {
            if (num[j] < num[minPos])
                minPos = j;
        }
        
        mySwap(num[i], num[minPos]);
    }
}

算法分析

时间复杂度：O ( n 2 )

空间复杂度：O ( 1 )

稳定性：不稳定排序

直接插入排序（Insertion Sort）

把第一个元素作为有序部分，从第二个元素开始将剩余元素逐个插入有序部分的合适位置

算法描述

• 从第一个元素开始，该元素可以认为已经被排序
• 取出下一个元素，在已经排序的元素序列中从后向前扫描
• 如果该元素（已排序）大于新元素，将该元素移到下一位置
• 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
• 将新元素插入到该位置后
• 重复步骤2~5

代码实现

// 直接插入排序
void InsertionSort(vector<int> &num) {
    int len = num.size();
    for (int i = 1; i < len; ++i) {
        int tmp = num[i];
        int j = i - 1;
        while (j >= 0 && num[j] > tmp) { //在找合适位置
            num[j + 1] = num[j]; //移动元素位置
            --j; //移动索引
        }

        num[j + 1] = tmp; //插入合适位置
    }
}

算法分析

时间复杂度：O ( n 2 )

空间复杂度：O ( 1 )

稳定性：稳定排序

希尔排序（Shell Sort）

希尔排序是简单插入排序改进后的版本

把记录按增量分组，对每组使用直接插入排序；当增量减至 1 时，整个文件恰被分成一组

算法描述

• 选择一个增量序列 t1，t2，…，tk，其中 ti > tj，tk = 1；
• 按增量序列个数 k，对序列进行 k 趟排序
• 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

动图演示

代码实现

void ShellSort(vector<int> &num) {
    int len = num.size();

    // 逐渐缩小间隔，最终为1
    for (int step = len / 2; step > 0; step /= 2) {
        for (int i = step; i < len; ++i) {
            int tmp = num[i];
            int j = i - step;
            while (j >= 0 && tmp < num[j]) {
                num[j + step] = num[j];
                j -= step;
            }
            num[j + step] = tmp;
        }
    }
}

算法分析

时间复杂度：O ( n 2 )

空间复杂度：O ( 1 ) O(1)O(1)

稳定性：不稳定排序

归并排序（Merge Sort）

即先使子序列有序，再使子序列段间有序

算法描述

• 长度为 n 输入序列分成两个长度为 n/2 子序列
• 对两个子序列分别采用归并排序
• 将两个排序好子序列合并成一个最终序列

代码实现

void Merge(int *arr, int n) {
    int temp[n]; // 辅助数组
    int b = 0;  // 辅助数组的起始位置
    int mid = n / 2;    // mid将数组从中间划分，前一半有序，后一半有序
    int first = 0, second = mid;    // 两个有序序列的起始位置
 
    while (first < mid && second < n) {
        if (arr[first] <= arr[second])   // 比较两个序列
            temp[b++] = arr[first++];
        else
            temp[b++] = arr[second++];
    }
 
    while(first < mid) temp[b++] = arr[first++]; // 将剩余子序列复制到辅助序列中 
    while(second < n) temp[b++] = arr[second++];
    
    for (int i = 0; i < n; ++i)    // 辅助序列复制到原序列
        arr[i] = temp[i];
}
 
void MergeSort(int *arr, int n) {
    if (n <= 1) return;  // 递归出口
    if (n > 1) {
        MergeSort(arr, n / 2);    // 对前半部分进行归并排序
        MergeSort(arr + n / 2, n - n / 2);    // 对后半部分进行归并排序
        Merge(arr, n);    // 归并两部分
    }
}

算法分析

时间复杂度：O ( n ∗ l o g n )

空间复杂度：O ( n )

稳定性：稳定排序

快速排序（Quick Sort）

从数组中选择一个元素，称为 基准。把数组中所有小于 基准 元素放左边，所有大于或等于 基准 元素放右边（此时 基准 元素位置有序，即无需再移动 基准 位置）

以 基准 为界把大数组切割成两个小数组（分割操作，partition），对 基准 左右两边数组进行递归操作，直到数组大小为1。此时每个元素都处于有序位置

算法描述

• 从数列中挑出一个元素，称为 基准（pivot）
• 重新排序数列，比基准值小在前，比基准值大在后
• 递归把小于基准值子数列和大于基准值子数列排序

代码实现

// 分割操作
int Partition(vector<int> &num, int left, int right) {
    int pivot = num[left];
    int i = left + 1, j = right;
   
    while (true) {
        // 向右找到第一个小于等于 pivot 的元素位置
        while (i <= j && num[i] <= pivot)
            ++i;
        // 向左找到第一个大于等于 pivot 的元素位置
        while(i <= j && num[j] >= pivot ) 
            --j;
        
        if(i >= j)
            break;

        // 交换两个元素的位置，使得左边的元素不大于pivot,右边的不小于pivot
        mySwap(num[i], num[j]);
    }
    
    // 使中轴元素处于有序的位置
    num[left] = num[j];  
    num[j] = pivot; //经过上面的循环, j 后面就全是大于或等于 pivot 的数
    
    return j;
}

// 快速排序
void QuickSort(vector<int> &num, int left, int right) {
    if (left < right) {
        // 获取中轴元素所处的位置并进行分割
        int mid = Partition(num, left, right);
        
        // 递归处理
        QuickSort(num, left, mid - 1);
        QuickSort(num, mid + 1, right);
    }
}

算法分析

时间复杂度：O ( n ∗ l o g n )

空间复杂度：O ( l o g n )

稳定性：不稳定排序

堆排序（Heap Sort）

堆的定义

本文的堆是指数据结构堆，不是内存模型的堆。堆是树型结构，满足 ① 堆是一棵完全树 ② 堆中任意节点值总不大于(不小于)其子节点值 ； 大顶堆的堆顶是最大值，小顶堆则是最小值 ，常见堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等

二叉堆定义

堆通过 数组 实现，父节点和子节点位置存在一定关系

有时将二叉堆第一个元素放在数组索引 0 位置，有时放在 1 位置

若第一个元素放在数组索引 0 位置，则父节点和子节点关系如下：

1、索引为 i 的左孩子的索引是 (2 * i + 1)

2、索引为 i 的左孩子的索引是 (2 * i + 2)

3、索引为 i 的父结点的索引是 floor(( i - 1) / 2) 向下取整

若第一个元素放在数组索引 1 位置，则父节点和子节点关系如下：

1、索引为 i 左孩子的索引是 2*i

2、索引为 i 右孩子的索引是 2 * i + 1

3、索引为 i 父结点的索引是 floor( i / 2)

二叉堆的图文解析

二叉堆核心是 添加 和 删除，以 最大堆 举例

添加

在最大堆 [90, 80, 70, 60, 40, 30, 20, 10, 50] 种添加 85，步骤如下

向最大堆添加数据时 ：先将数据加到最大堆末尾，然后尽可能把这个元素往上挪，直至挪不动

删除

在最大堆 [90, 85, 70, 60, 80, 30, 20, 10, 50, 40] 中删除 90，步骤如下

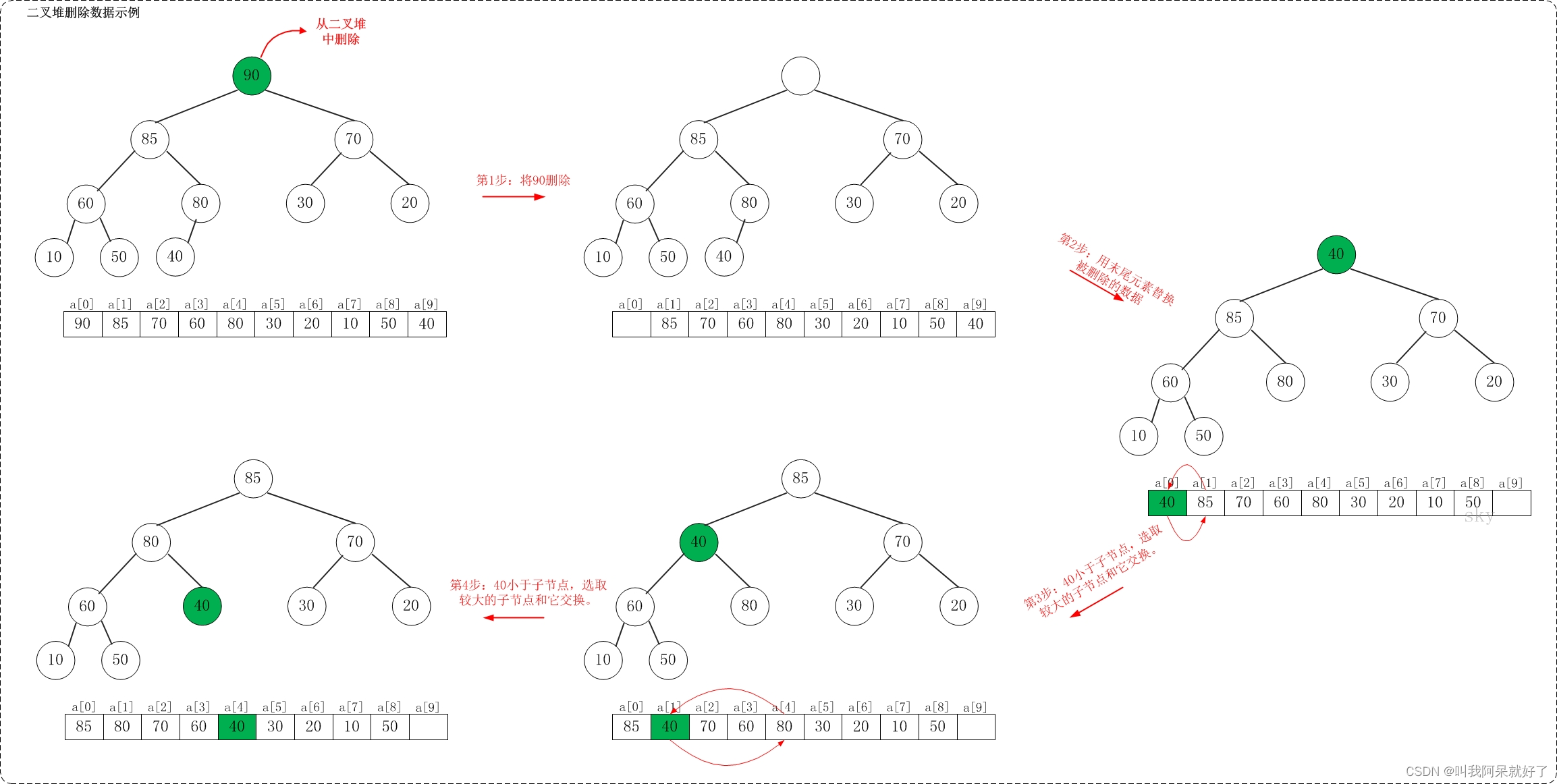
从最大堆中删除数据，先删除该数据，然后用最大堆中最后一个元素插入这个空位；接着，把这个 空位 尽量往上挪，直到剩余数据变成一个最大堆（替换后树仍要是最大堆）

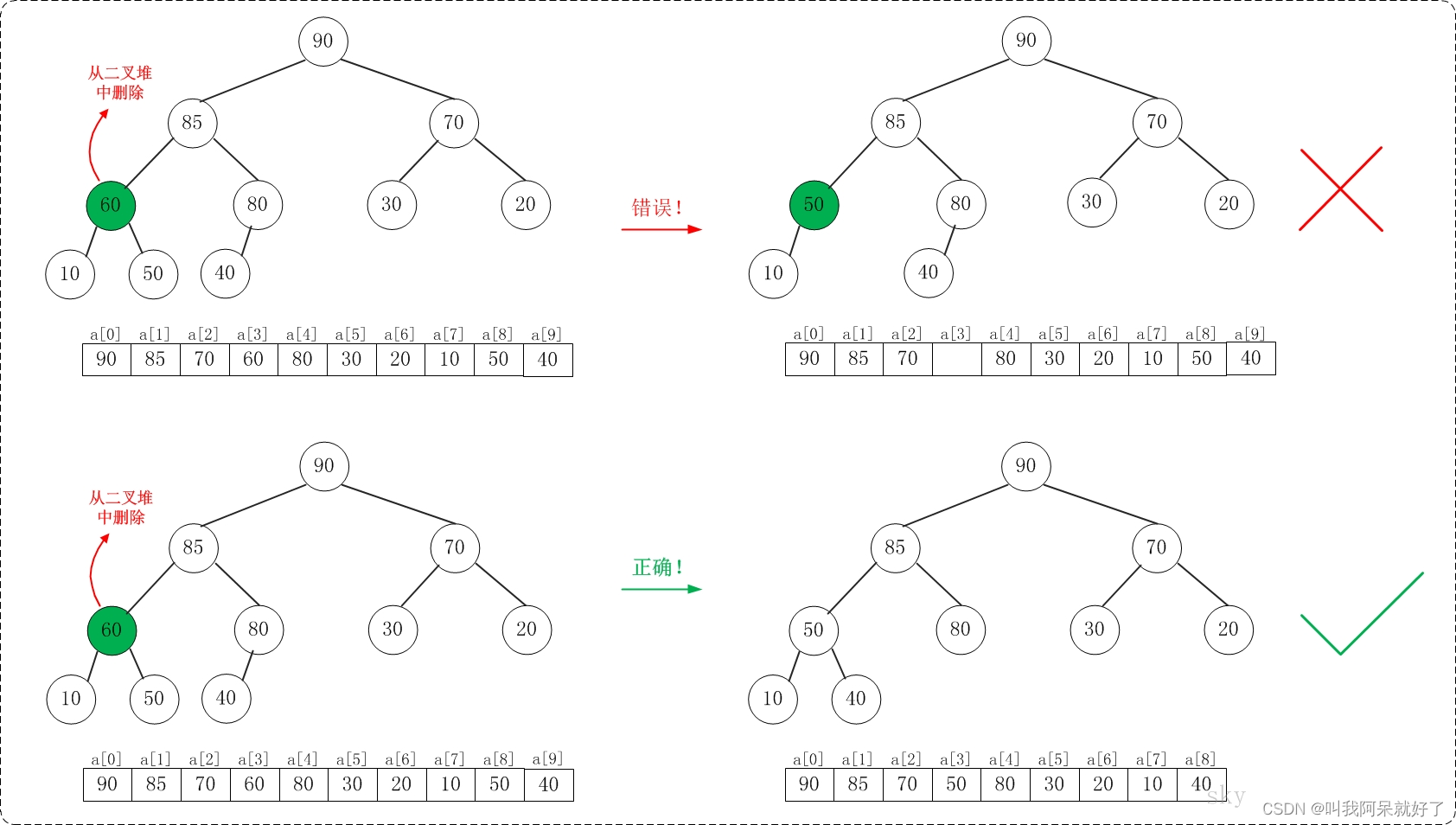
堆排，把堆顶元素与最后一个元素交换，交换后破坏堆特性，把堆中元素再次构成大顶堆，然后把堆顶元素与最后第二个元素交换，循环至剩余元素只有一个

// 下沉操作
void downAdjust(vector<int> &num, int parent, int n) {  
    // 临时保存要下沉的元素  
    int temp = num[parent];      
    // 定位左孩子节点的位置
    int child = 2 * parent + 1;    
    
    // 开始下沉
    while (child <= n) {
        // 如果右孩子节点比左孩子大，则定位到右孩子
        if (child + 1 <= n && num[child] < num[child + 1])
            ++child;
        
        // 如果孩子节点小于或等于父节点，则下沉结束
        if (num[child] <= temp) 
            break;
        
        // 父节点进行下沉
        num[parent] = num[child];
        parent = child;
        child = 2 * parent + 1;
    }
    num[parent] = temp; //更新当前下沉值
}

void HeapSort(vector<int> &num) {
    int len = num.size();
    
    // 构建大顶堆
    for (int i = (len - 2) / 2; i >= 0; --i) {
        downAdjust(num, i, len - 1);
    }
    
    // 进行堆排序
    for (int i = len - 1; i >= 1; --i) {
        // 把堆顶元素与最后一个元素交换
        mySwap(num[0], num[i]);
        // 把打乱的堆进行调整，恢复堆的特性
        downAdjust(num, 0, i - 1);
    }
}

算法分析

时间复杂度：O ( n ∗ l o g n )

空间复杂度：O ( 1 )

稳定性：不稳定排序

计数排序（Counting Sort）

适合最大值和最小值差值不是很大的情况。把数组元素作为数组的下标，然后用一个临时数组统计该元素出现的次数，例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来，此时汇总起来是数据是有序的

代码实现

// 计数排序
void CountingSort(vector<int> &num) { 
    int len = num.size();
    
    // 得到数列的最大和最小值
    int max = num[0], min = num[0];  
    for (int i = 1; i < len; ++i) {        
        if(num[i] > max)           
            max = num[i];        
        
        if (num[i] < min)
            min = num[i];
    }
    
    // 根据数列最大值确定统计数组的长度
    vector<int> countArray(max - min + 1, 0);
    
    // 遍历数列，填充统计数组
    for (int i = 0; i < len; ++i) {
        countArray[num[i] - min]++;
    }
    
    // 遍历统计数组，输出结果   
    int index = 0;  
    for (int i = 0; i < countArray.size(); ++i) {
        for (int j = 0; j < countArray[i]; ++j) {
            num[index++] = i + min;
        }
    }
}

算法分析

时间复杂度：O ( n + k ) ，其中 k 为临时数组大小

空间复杂度：O ( k )

稳定性：稳定排序

桶排序（Bucket Sort）

把最大值和最小值之间数进行瓜分，例如分成 10 个区间，10个区间对应10个桶，把各元素放到对应区间桶中，再对每个桶中的数进行排序，可以采用归并排序、快速排序等方法。之后每个桶里面的数据就是有序的了，按顺序遍历各桶即可得到排序序列（桶排序也可用于浮点数排序）

动图演示

代码实现

// 桶排序
// 有负数的话需要进行预处理, 本函数包含预处理部分
void BucketSort(vector<int> &num) {   
    int len = num.size();
    
    // 得到数列的最大最小值
    int max = num[0], min = num[0];  
    for(int i = 1; i < len; ++i) {        
        if(num[i] > max)           
            max = num[i];        
        
        if (num[i] < min)
            min = num[i];
    }
    
    // 计算桶的数量并初始化
    int bucketNum = (max - min) / len + 1;
    vector<int> vec;
    vector<vector<int>> bucket;
    for (int i = 0; i < bucketNum; ++i)
        bucket.push_back(vec);
    
    // 将每个元素放入桶
    for (int i = 0; i < len; ++i) {
        // 减去最小值，处理后均为非负数
        int pos = (num[i] - min) / len;
        bucket[pos].push_back(num[i]);
    }
    
    // 对每个桶进行排序，此处可选择不同排序方法
    for (int i = 0; i < bucket.size(); ++i) 
        sort(bucket[i].begin(), bucket[i].end());
    
    // 将桶中的元素赋值到原序列
	int index = 0;
	for (int i = 0; i < bucketNum; ++i)
		for(int j = 0; j < bucket[i].size(); ++j)
			num[index++] = bucket[i][j];
}

算法分析

时间复杂度：O ( n + k )

空间复杂度：O ( k )

稳定性：稳定排序

基数排序（Radix Sort）

先以个位数的大小来对数据进行排序，接着以十位数的大小来进行排序，接着以百位数的大小 ……

以某位数进行排序时，用 桶 来排序，由于某位数（个位/十位….，不是一整个数）的大小范围为0~9，所以我们需要10个桶，然后把具有相同数值数放进同一个桶里，之后再把桶里的数按照 0 号桶到 9 号桶的顺序取出来。一趟下来按照某位数的排序就完成了

代码实现

// 基数排序
// 有负数的话需要进行预处理，本函数不包含预处理部分
void RadixSort(vector<int> &num) {
    int len = num.size();
    
    // 得到数列的最大值
    int max = num[0];  
    for (int i = 1; i < len; ++i) {        
        if(num[i] > max)           
            max = num[i];
    }

    // 计算最大值是几位数
    int times = 1;
    while (max / 10 > 0) {
        ++times;
        max /= 10;
    }

     // 创建10个桶
    vector<int> vec;
    vector<vector<int>> bucket;
    for (int i = 0; i < 10; ++i) {
        bucket.push_back(vec);
    }
    
    // 进行每一趟的排序，从个位数开始排
    for (int i = 1; i <= times; i++) {
        for (int j = 0; j < len; j++) {
            // 获取每个数最后第 i 位对应桶的位置
            int radio = (num[j] / (int)pow(10,i-1)) % 10;
            // 放进对应的桶里
            bucket[radio].push_back(num[j]);
        }
        // 合并放回原数组
        int k = 0;
        for (int j = 0; j < 10; j++) {
            for (int& t : bucket[j]) {
                num[k++] = t;
            }
            //合并之后清空桶
            bucket[j].clear();
        }  
    }
}

算法分析

时间复杂度：O ( k ∗ n )

空间复杂度：O ( k + n )

稳定性：稳定排序

三 🏠 结语

身处于这个浮躁的社会，却有耐心看到这里，你一定是个很厉害的人吧 👍👍👍

各位博友觉得文章有帮助的话，别忘了点赞 + 关注哦，你们的鼓励就是我最大的动力

博主还会不断更新更优质的内容，加油吧！技术人！ 💪💪💪