文章目录
- Notation
- Backpropagation
- Forward pass
- Backward pass
- Summary
Notation
神经网络求解最优化Loss function时参数非常多,反向传播使用链式求导的方式提升计算梯度向量时的效率,链式法则如下:
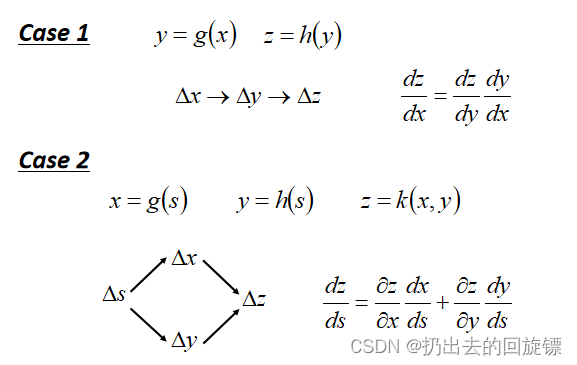
Backpropagation
损失函数计算为所有样本的损失之和,即样本预测值与实际值之间的差距(通常是交叉熵),函数表示如下:
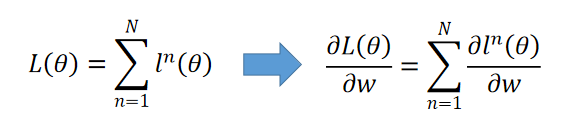
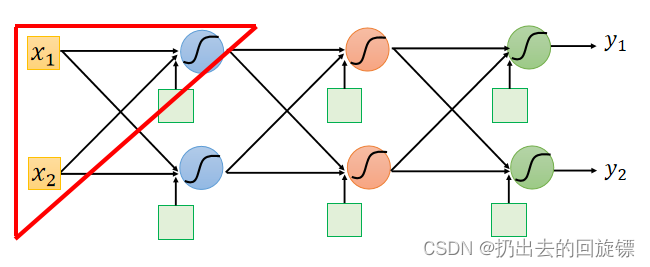
考虑第一个neural:
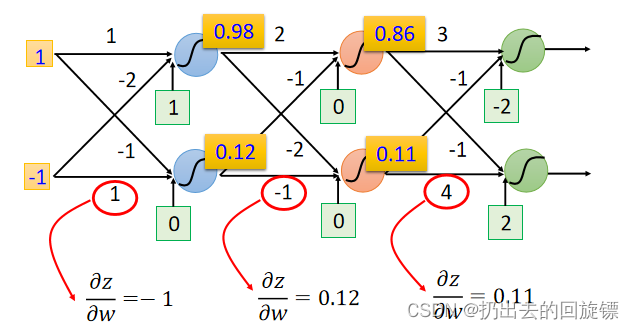
由链式法则有:
∂
l
∂
w
=
∂
z
∂
w
∂
l
∂
z
\frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z}
∂w∂l=∂w∂z∂z∂l
其中
∂
z
∂
w
\frac{\partial z}{\partial w}
∂w∂z被称为forward pass,
∂
l
∂
z
\frac{\partial l}{\partial z}
∂z∂l被称为backward pass
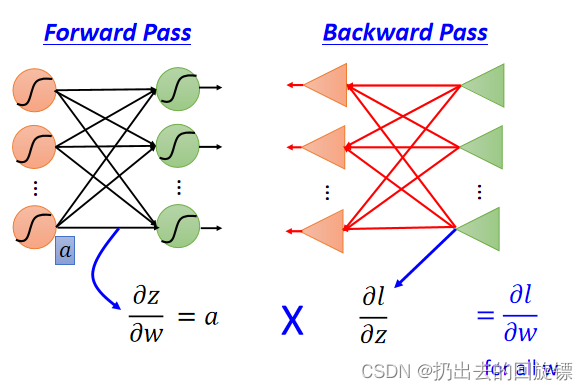
Forward pass
这一部分计算相当容易,显然等于input的值。即使在中间的neural也是如此,直观图如下:
Backward pass
继续链式法则展开:
∂
l
∂
z
=
∂
a
∂
z
∂
l
∂
a
\frac{\partial l}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial l}{\partial a}
∂z∂l=∂z∂a∂a∂l
直观图表示如下:
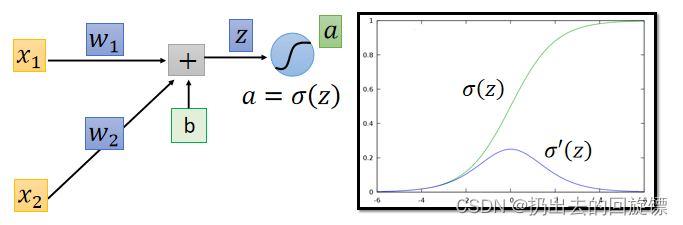
继续展开第二项:
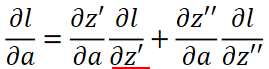
直观图如下:
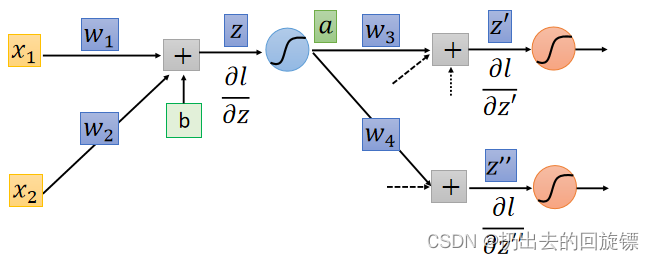
此时结果表示为:
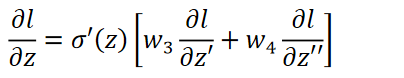
其中
σ
′
(
z
)
\sigma{'} (z)
σ′(z)在Forward 的过程过程中已经计算出来了,即:
σ
(
z
)
(
1
−
σ
(
z
)
)
\sigma(z)(1-\sigma(z))
σ(z)(1−σ(z))两个未知项分类讨论有:
Case 1. Output Layer
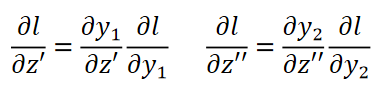
Case 2. Not Output Layer
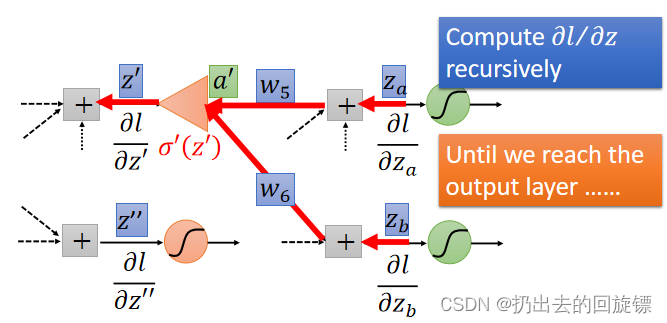
实际上进行backward pass是反向的计算,即从output layer算
Summary