1.题目

数学老师给小明出了一道等差数列求和的题目。

但是粗心的小明忘记了一部分的数列，只记得其中 N个整数。

现在给出这 N个整数，小明想知道包含这 N 个整数的最短的等差数列有几项？

输入格式
输入的第一行包含一个整数 N。

第二行包含 N 个整数 A1,A2,⋅⋅⋅,AN。(注意 A1∼AN 并不一定是按等差数列中的顺序给出)

输出格式
输出一个整数表示答案。

数据范围
$2\le N\le 100000$,
$0\le Ai\le 10^9$

输入样例：

5
2 6 4 10 20

输出样例：

10

样例解释:

包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、18、20。

2.基本思想

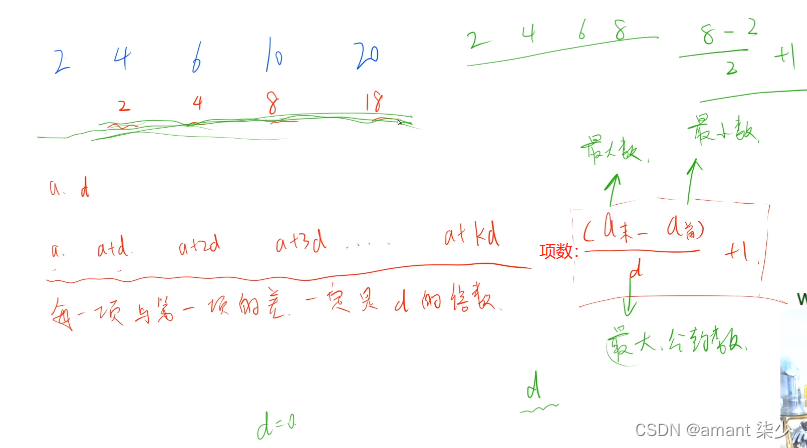
$每一项与第一项的差一定是d的倍数$
$当d！=0时，(a末-a初)/d+1----让公差d最大即可$
$当d==0时，答案为n$

3.代码实现

import java.util.Arrays;
import java.util.Scanner;

public class _1246等差数列 {
    static Scanner sc = new Scanner(System.in);
    static int N = 100010;
    static int a[] = new int[N];

    public static void main(String[] args) {
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) a[i] = sc.nextInt();
        Arrays.sort(a, 1, n + 1);
        int d = 0;
        //通过 最大公约数 求出 公差d
        for (int i = 2; i <= n ; i++) d = gcd( a[i] - a[1],d);

        if (d == 0) System.out.println(n);
        else System.out.println((a[n] - a[1]) / d + 1);
    }

    public static int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}