一、题目

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

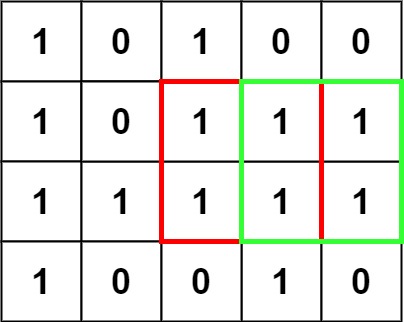
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

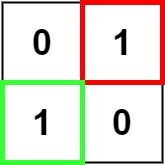
输入：matrix = [["0","1"],["1","0"]]

输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

二、代码

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        // dp[i][j]：正方形必须以（i，j）位置作为右下角，所有可能的正方形里最大的内部全是1的正方形边长有多长
        int[][] dp = new int[n][m];
        // 记录当前收集到的最大正方形的边长
        int max = 0;

        // 赋初值
        // 第一行和第一列的格子作为正方形的右下角，一定最多只能形成边长为1的正方形
        for (int j = 0; j < m; j++) {
            // 如果这个位置为1，那么形成的最大正方形边长就是1
            dp[0][j] = matrix[0][j] == '1' ? 1 : 0;
            // 同步更新max
            if (max < dp[0][j]) {
                max = 1;
            }
        }
        for (int i = 1; i < n; i++) {
            // 如果这个位置为1，那么形成的最大正方形边长就是1
            dp[i][0] = matrix[i][0] == '1' ? 1 : 0;
            // 同步更新max
            if (max < dp[1][0]) {
                max = 1;
            }
        }

        // 构造dp数组
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                // 如果当前位置是1，再从左边、上边、左上角三个正方形中求最小正方形的边长是多少，假设是a，那么当前位置的最大正方形边长就是a+1
                // 如果当前位置不是1，那么无法以该位置为正方形的右下角来形成一个内部都是1的正方形，所以边长为0
                dp[i][j] = matrix[i][j] == '1' ? Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1 : 0;
                // 更新max
                if (max < dp[i][j]) {
                    max = dp[i][j];
                }
            }
        }
        // 返回最大面积
        return max * max;
    }
}