以前只知道工业控制中用的是PID控制,然而最近了解到实际生产中还在使用ADRC控制,而且使用效果还优于PID控制,遂找了几篇文献学习学习。
0 引言
自抗扰控制(Active Disturbances Rejection Controller,ADRC)技术,是发扬PID控制技术的精髓并且吸取了现代控制理论,不依赖于被控对象精确模型,能够替代PID控制技术,是一种新型的实用数字控制技术。
PID控制的缺点:
①直接以
e
=
v
−
y
e=v-y
e=v−y 的方式产生原始误差不太合理,因为控制目标
v
v
v 是可以跳变的,而对象输出
y
y
y 是存在惯性的,不可能跳变,所以让缓变的
y
y
y 来跟踪能跳变的
v
v
v 是不合理的。
② 由于微分器物理不可实现,只能近似实现,所以产生误差的微分信号
d
e
/
d
t
\mathrm{d}e/\mathrm{d}t
de/dt 是不合适的,并且微分信号容易被噪声干扰。
③线性组合不一定是最好的组合办法。
④误差信号
e
e
e 的积分
∫
0
∝
e
(
t
)
d
t
\int\limits_0^{\propto}{e\left( t \right) \mathrm{d}t}
0∫∝e(t)dt 的引入有很多负作用,其能使闭环变得迟钝,容易产生振荡。
因此,基于PID控制的思想,并且利用现代数字信号处理技术,开发出新型实用数字控制技术——ADRC自抗扰控制。
1 空气起动系统模型
空气起动系统模型见:【空气起动系统控制】使用神经网络PID调节起动机入口压力值
2 ADRC控制器设计
自抗扰控制器(ADRC)主要包括由安排过度过程减少输入对系统的冲击以及提取微分信号的跟踪微分器TD;对系统状态观测和扰动估计的扩张状态观测器ESO;实时动态反馈的状态误差反馈控制NLSEF三个部分,结构图如下图所示。
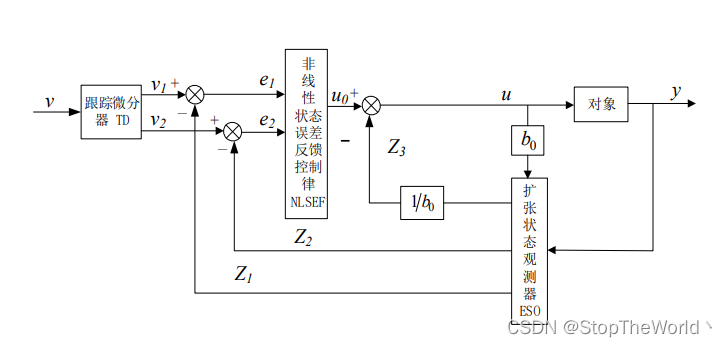
2.1 跟踪微分器TD
跟踪微分器(Tracking Differentiator)可以对输入信号进行预处理,其能够快速的跟踪给定的输入信号,并且能够通过非线性最速函数迭代的方式得到输入的微分,而不是直接应用微分器的方式得到输入的微分,减少了噪声信号的干扰。一般二阶形式如下:
{
v
˙
1
=
v
2
v
˙
2
=
f
h
f
h
=
f
h
a
n
(
v
1
−
v
0
,
v
2
,
r
,
h
0
)
\begin{cases} \dot{v}_1=v_2\\ \dot{v}_2=fh\\ fh=fhan\left( v_1-v_0, v_2, r, h_0 \right)\\ \end{cases}
⎩
⎨
⎧v˙1=v2v˙2=fhfh=fhan(v1−v0,v2,r,h0)
v
0
v_0
v0 输入信号,
v
1
v_1
v1 输入信号的跟踪信号,
v
2
v_2
v2 输入信号的微分信号,
r
r
r 速度因子,
h
0
h_0
h0 滤波因子,
f
h
a
n
fhan
fhan 为非线性的最速控制综合函数,能够实现对期望输入的平稳快速跟踪,且对输入信号的噪声具有一定的抑制效果。
f
h
a
n
(
v
1
−
v
0
,
v
2
,
r
,
h
0
)
=
{
f
s
g
(
x
,
d
)
=
(
s
i
g
n
(
x
+
d
)
−
s
i
g
n
(
x
−
d
)
)
/
2
d
=
r
h
2
a
0
=
h
0
x
2
y
=
x
1
+
a
0
a
1
=
d
(
d
+
8
∣
y
∣
)
a
2
=
a
0
+
s
i
g
n
(
y
)
(
a
1
−
d
)
/
2
a
=
(
a
0
+
y
)
f
s
g
(
y
,
d
)
+
a
2
(
1
−
f
s
g
(
y
,
d
)
)
f
h
a
n
=
−
r
(
a
d
)
f
s
g
(
a
,
d
)
−
r
s
i
g
n
(
a
)
(
1
−
f
s
g
(
a
,
d
)
)
fhan\left( v_1-v_0, v_2, r, h_0 \right) =\left\{ \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{array}{c} fsg\left( x,d \right) =\left( \mathrm{sign}\left( x+d \right) -\mathrm{sign}\left( x-d \right) \right) /2\\ d=rh^2\\ \end{array}\\ a_0=h_0x^2\\ \end{array}\\ y=x_1+a_0\\ \end{array}\\ \begin{array}{c} \begin{array}{c} a_1=\sqrt{d\left( d+8\left| y \right| \right)}\\ a_2=a_0+\mathrm{sign}\left( y \right) \left( a_1-d \right) /2\\ \end{array}\\ a=\left( a_0+y \right) fsg\left( y,d \right) +a_2\left( 1-fsg\left( y,d \right) \right)\\ fhan=-r\left( \frac{a}{d} \right) fsg\left( a,d \right) -r\mathrm{sign}\left( a \right) \left( 1-fsg\left( a,d \right) \right)\\ \end{array}\\ \end{array} \right.
fhan(v1−v0,v2,r,h0)=⎩
⎨
⎧fsg(x,d)=(sign(x+d)−sign(x−d))/2d=rh2a0=h0x2y=x1+a0a1=d(d+8∣y∣)a2=a0+sign(y)(a1−d)/2a=(a0+y)fsg(y,d)+a2(1−fsg(y,d))fhan=−r(da)fsg(a,d)−rsign(a)(1−fsg(a,d))
2.2 扩张状态观测器ESO
扩张状态观测器(Extended State Observer)是将除了串联积分标准型以外的模型部分和外界扰动当作一个新的状态,进行观测。对于二阶系统,ESO 的标准形式为
{
e
=
z
1
−
y
z
˙
1
=
z
2
−
β
01
e
z
˙
2
=
z
3
−
β
02
f
a
l
(
e
,
α
01
,
δ
01
)
+
b
0
u
z
˙
3
=
−
β
03
f
a
l
n
(
e
,
α
02
,
δ
02
)
\begin{cases} \begin{array}{l} \begin{array}{l} e=z_1-y\\ \dot{z}_1=z_2-\beta _{01}e\\ \end{array}\\ \dot{z}_2=z_3-\beta _{02}fal\left( e,\alpha _{01},\delta _{01} \right) +b_0u\\ \end{array}\\ \dot{z}_3=-\beta _{03}fal_n\left( e,\alpha _{02},\delta _{02} \right)\\ \end{cases}
⎩
⎨
⎧e=z1−yz˙1=z2−β01ez˙2=z3−β02fal(e,α01,δ01)+b0uz˙3=−β03faln(e,α02,δ02) 其中非线性函数
f
a
l
fal
fal 为
f
a
l
(
x
,
α
,
δ
)
=
{
∣
x
∣
α
s
i
g
n
(
x
)
,
∣
x
∣
⩾
δ
x
/
δ
1
−
α
,
∣
x
∣
<
δ
fal\left( x,\alpha ,\delta \right) =\begin{cases} \left| x \right|^{\alpha}\mathrm{sign}\left( x \right) , \left| x \right|\geqslant \delta\\ x/\delta ^{1-\alpha}, \left| x \right|<\delta\\ \end{cases}
fal(x,α,δ)={∣x∣αsign(x),∣x∣⩾δx/δ1−α,∣x∣<δ
β
01
\beta _{01}
β01,
β
02
\beta _{02}
β02, …,
β
0
n
\beta _{0n}
β0n 为ESO的增益,其值对ESO的观测能力和估计扰动的能力起决定性作用。
e
e
e 为观测误差,
δ
0
i
\delta _{0i}
δ0i 为观测误差的线性变化区域的大小,
α
0
i
\alpha _{0i}
α0i 代表误差指数变化的参数,
b
0
b _{0}
b0 为控制增益的估计值。ESO不仅能够观测出状态变量
x
(
n
)
x^{\left( n \right)}
x(n) 和
z
n
z_n
zn 还能估计出系统总扰动
z
n
+
1
z_{n+1}
zn+1,其中总扰动包括已建动力学模型、模型不确定性和外部干扰等因素。
2.3 非线性反馈
非线性反馈(Nonlinear State Error Feedback)是保留了PID基于误差消除误差的部分,与 PD 控制不同的是加入了非线性函数,不再是原来线性组合的方式,利用非线性函数的性质实现更高精度的控制,常用的控制器主要为:
{
e
1
=
v
1
−
z
1
e
2
=
v
2
−
z
2
u
0
=
β
1
f
a
l
(
e
1
,
α
1
,
δ
1
)
+
β
2
f
a
l
(
e
2
,
α
2
,
δ
1
)
\begin{cases} e_1=v_1-z_1\\ e_2=v_2-z_2\\ u_0=\beta _1fal\left( e_1,\alpha _1,\delta _1 \right) +\beta _2fal\left( e_2,\alpha _2,\delta _1 \right)\\ \end{cases}
⎩
⎨
⎧e1=v1−z1e2=v2−z2u0=β1fal(e1,α1,δ1)+β2fal(e2,α2,δ1) 其中,
v
i
v_i
vi 为TD输出信号,
z
i
z_i
zi 为ESO的输出,
β
i
\beta_i
βi 为非线性反馈的增益,
f
a
l
fal
fal 函数见上。
2.4 扰动补偿
扰动补偿部分是 ADRC 控制器最为核心思想。通过 ESO 实时观测扰动并在控制输入端实时补偿,在扰动对系统产生影响前补偿到控制输入端。针对二阶系统,
z
3
z_3
z3 是对总扰动的估计,所以控制量为
u
=
u
0
−
z
3
/
b
0
u=u_0-z_3/b_0
u=u0−z3/b0 其中,
b
0
b_0
b0 为补偿因子,与ESO中的参数
b
0
b_0
b0 一致,适当调节可得到最终的控制效果。
另外,TD、ESO、NLSEF的参数整定方法见空气起动系统仿真下面的 NLSEF.m 脚本说明。
3 仿真结果
将本文的控制方法与之前使用的PID控制器、RBF-PID控制器进行对比,在相同的参数下,仿真结果如下
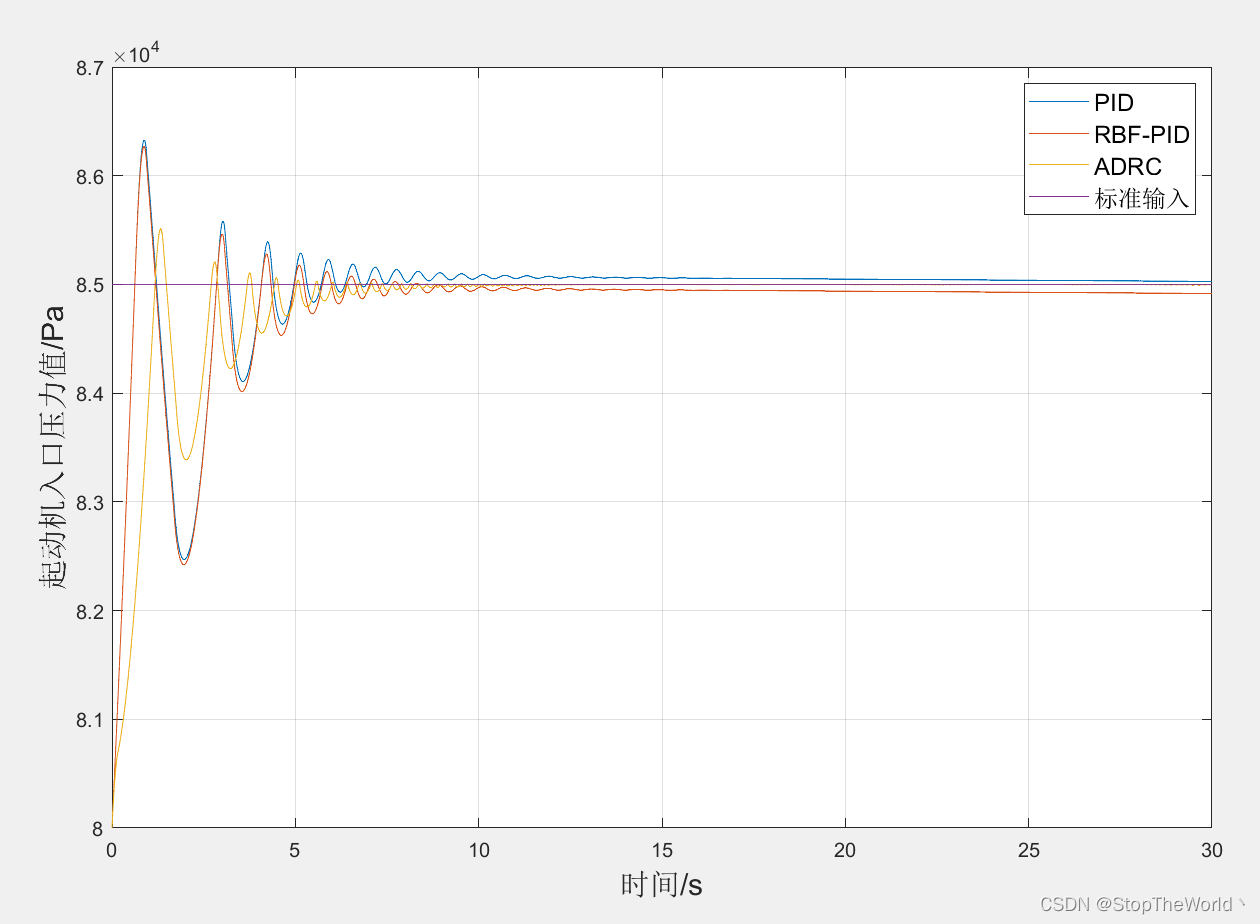
结论:由图可得,ADRC控制器相比于另外两种控制器,其超调量更小,稳态误差也更小,调节时间也更短,有明显的性能改善,初步验证了ADRC控制在理论上的可行性。
4 未来工作
由于ADRC控制相比PID控制在基础理论层面和仿真层面上有明显的改善,所以下一步工作准备将ADRC控制应用于实际工程上,使用PLC程序编写ADRC控制代码以替换掉原来的PID控制程序,看看ADRC的实际控制结果究竟如何。