CSDN每日一练：蛇形矩阵

news2024/10/5 15:25:25

题目名称：蛇形矩阵
时间限制：1000ms内存限制：256M
题目描述
给你一个整数n，输出n∗n的蛇形矩阵。

输入描述：
输入一行，包含一个整数n

输出描述：
输出n行，每行包含n个正整数，通过空格分隔。

示例
示例1
输入
4
输出
1 2 6 7
3 5 8 13
4 9 12 14
10 11 15 16

提示
无

嗯，这个题目其实不算复杂，嗯，想起来一个菱形的题目，和这个差不多

矩阵
1 2
3 4
菱形
　1
3 　 2
　4

矩阵
1 2 6
3 5 7
4 8 9
菱形
　　1
　3 　 2
4 　 5 　 6
　8　 7
　　9

先不管顺序问题，这个数字填写得数量都是一致的了，菱形偶数行(0,2,4…)填写单数个数字，需要正向填写，单数行(1,3,5…)逆向填写

所以，第一个版本的方法就出来了

n = 6
dp = [[0]*n for _ in range(n)]
s = 0
for i in range(n):
    for j in range(i+1):
        s += 1
        if i % 2 == 0:
            dp[i - j][j] = s
        else:
            dp[j][i - j] = s
            
print('\n'.join([' '.join([str(i) for i in j]) for j in dp]))

在这里插入图片描述

菱形的上半部分就算完成了，不过把菱形的位置换算成了矩阵的位置
然后，再循环一次，将后半部分补全，用长度n来减去行列下标得到后半的下标就可以补全了

n = 8
dp = [[0]*n for _ in range(n)]
s = 0
for i in range(n):
    for j in range(i+1):
        s += 1
        if i % 2 == 0:
            dp[i - j][j] = s
        else:
            dp[j][i - j] = s

for i in range(n-1,0,-1):
    for j in range(j):
        s+=1
        if i % 2 == 0:
            dp[n-i+j][n-j-1] = s
        else:
            dp[n-j-1][n-i+j] = s

print('\n'.join([' '.join([str(i) for i in j]) for j in dp]))

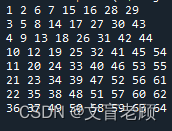
在这里插入图片描述
其实，到了这里，提交就已经可以通过了，但是，需要前半部分和后半部分分开计算。。。。老顾突然脑子就又抽抽了一下，想弄一个可以直接两层循环全部填完的办法

主要想法来源是，第二行的数字，都是上一行后一位的数字要么加1，要么减1。。。。。。
于是就需要先把第一行的数字全都计算出来了，经过一番研究，发现第一行偶数位置的数字存在一个规律

1 1 + 0 * 4
6 1 + 0 * 4 + 1 + 1 * 4
15 1 + 0 * 4 + 1 + 1 * 4 + 1 + 2 * 4
28 1 + 0 * 4 + 1 + 1 * 4 + 1 + 2 * 4 + 1 + 3 * 4

所以，第一行的数字就得出来了，比如n=10的时候

n = 10

j = 0
t = []
for i in range(n):
    j += i*4+1
    t.append(j)
# t = [1,6,15,28,45,66,91,120,153,190]

所以，第一行的数字，也出来了

1 2 6 7 15 16 28 29 45 46 66 67 91 92 120 121 153 154 190 191

嗯，这个数字实际上是n的2倍了。。。计算第一行数字时，忘记减半计算了，算了，就这样把

生成一个二维数组，然后把第一行数字填上去

n = 10

j = 0
t = []
for i in range(n):
    j += i*4+1
    t.append(j)

dp = [[0]*n for _ in range(n)]
for j in range(n):
    if j%2==0:
        dp[0][j] = t[j//2]
    else:
        dp[0][j] = t[j//2]+1

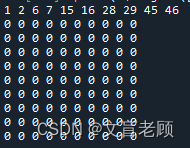
在这里插入图片描述
然后计算第二行的数字，如果不是最后一列，基本上可以从上一行的数字得到该位置的数字，所以得到第一部分计算

for i in range(1,n):
    for j in range(n):
        if j<n-1:
            if (i+j)%2==0:
                dp[i][j] = dp[i-1][j+1]-1
            else:
                dp[i][j] = dp[i-1][j+1]+1

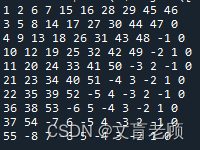
在这里插入图片描述
因为正好第二行最后一个数字无法从上一行取得，所以后半部分得到的数字都是错的
然后，我们发现，另外的规律，第二行加第十列（1+9）是偶数，则无法从上一行最后一列的数字得到结果，是单数行时，则可以直接用上一行的数字加1得到结果，所以先完成单数行的计算，这次我们把 n 设置成一个单数，然后行列和为单数的先完成

n = 9

j = 0
t = []
for i in range(n):
    j += i*4+1
    t.append(j)

dp = [[0]*n for _ in range(n)]
for j in range(n):
    if j%2==0:
        dp[0][j] = t[j//2]
    else:
        dp[0][j] = t[j//2]+1
    

for i in range(1,n):
    for j in range(n):
        if j<n-1:
            if (i+j)%2==0:
                dp[i][j] = dp[i-1][j+1]-1
            else:
                dp[i][j] = dp[i-1][j+1]+1
        elif (i+j)%2==1:
            dp[i][j] = dp[i-1][j]+1

print('\n'.join([' '.join([str(i) for i in j]) for j in dp]))

在这里插入图片描述
最后，想办法得到偶数行最后一列的数字，嗯。。。。。推算出一个公式。。。偶数行最后一列的数字是

n**2 - (n-行号)**2+(n-行号)//2
注：行列和为偶数时计算最后一列数字

嗯。。。脑子抽抽了猜去研究这个怎么计算，最后得到完整结果

n = 9

j = 0
t = []
for i in range(n):
    j += i*4+1
    t.append(j)

dp = [[0]*n for _ in range(n)]
for j in range(n):
    if j%2==0:
        dp[0][j] = t[j//2]
    else:
        dp[0][j] = t[j//2]+1
    

for i in range(1,n):
    for j in range(n):
        if j<n-1:
            if (i+j)%2==0:
                dp[i][j] = dp[i-1][j+1]-1
            else:
                dp[i][j] = dp[i-1][j+1]+1
        elif (i+j)%2==1:
            dp[i][j] = dp[i-1][j]+1
        else:
            dp[i][j] = n**2-(n-i)*(n-i)//2+(n-i)//2


print('\n'.join([' '.join([str(i) for i in j]) for j in dp]))