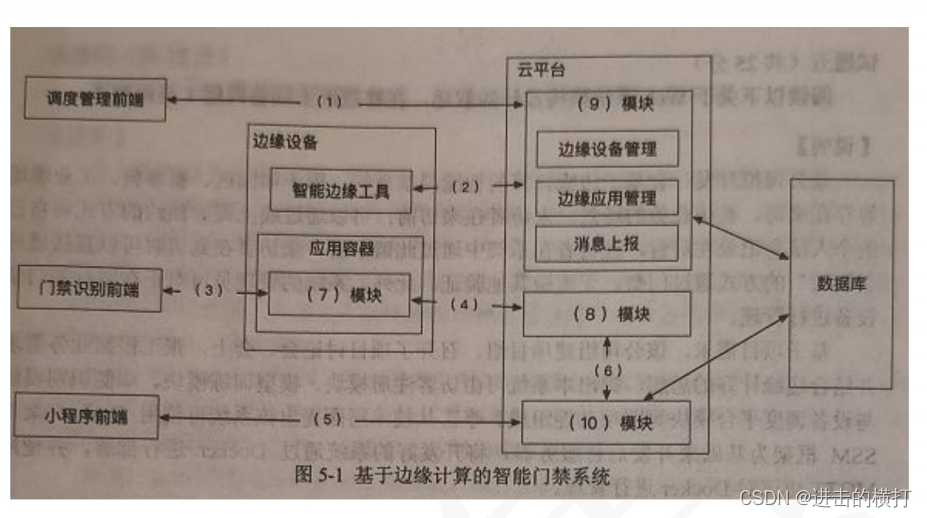
指派问题概述:
实际中,会遇到这样的问题,有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每行每列各有1个元素,使得和最小。
如下图:
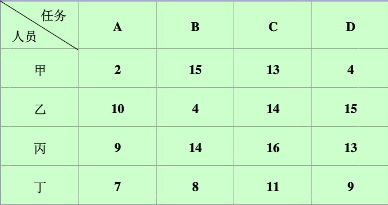
指派问题性质:
指派问题的最优解有这样一个性质,若从矩阵的一行(列)各元素中分别减去该行(列)的最小元素,得到归约矩阵,其最优解和原矩阵的最优解相同.
匈牙利法:
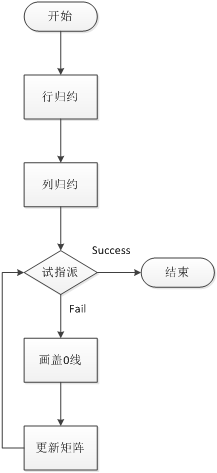
12 | 7 | 9 | 7 | 9 |
8 | 9 | 6 | 6 | 6 |
7 | 17 | 12 | 14 | 9 |
15 | 14 | 6 | 6 | 10 |
4 | 10 | 7 | 10 | 9 |
1.行归约:
每行元素减去该行的最小元素
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
2.列归约:
每列元素减去该列的最小元素
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
3.试指派:
(1)找到未被画线的含0元素最少的行列,即,遍历所有未被画线的0元素,看下该0元素所在的行列一共有多少个0,最终选取最少个数的那个0元素。
(2)找到该行列中未被画线的0元素,这就是一个独立0元素。对该0元素所在行和列画线。
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
(3)暂时不看被线覆盖的元素,重复(1)(2)直到没有线可以画。
(4)根据(2)找到的0元素个数判断,找到n个独立0元素则Success,小于n个则Fail.(本例子中,n=5,可以看到,第一次试指派之后,独立0元素有4个,不符合)
4.画盖0线:
目标:做最少的直线数覆盖所有0元素,直线数就是独立0元素的个数。
注意:这跟3的线不同;不能用贪心法去画线,比如
1 0 0
1 1 0
1 0 1
若先画横的,则得画3条线,实际只需2条;若先画竖的,将矩阵转置后同理。
步骤3得出的独立0元素的位置
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
(1)对没有独立0元素的行打勾、
(2)对打勾的行所含0元素的列打勾
(3)对所有打勾的列中所含独立0元素的行打勾
(4)重复(2)(3)直到没有不能再打勾
(5)对打勾的列和没有打勾的行画画线,这就是最小盖0线。
5 | 0 | 2 | 0 | 2 | |
2 | 3 | 0 | 0 | 0 | |
0 | 10 | 5 | 7 | 2 | √ |
9 | 8 | 0 | 0 | 4 | |
0 | 6 | 3 | 6 | 5 | √ |
√ |
5 | 0 | 2 | 0 | 2 | |
2 | 3 | 0 | 0 | 0 | |
0 | 10 | 5 | 7 | 2 | √ |
9 | 8 | 0 | 0 | 4 | |
0 | 6 | 3 | 6 | 5 | √ |
√ |
5.更新矩阵:
(1)对没有被线划到的数中,找到最小的数。
(2)对没有被线划到的数中,减去最小的数。
(3)对被2条线划到的数中,加上最小的数。
7 | 0 | 2 | 0 | 2 |
4 | 3 | 0 | 0 | 0 |
0 | 8 | 3 | 5 | 0 |
11 | 8 | 0 | 0 | 4 |
0 | 4 | 1 | 4 | 3 |
6.重复3-5直到成功。
0 | 1 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 0 | 0 | 1 |
0 | 0 | 0 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
sum = 7+6+9+6+4 = 32
匈牙利算法(Hungarian Algorithm)
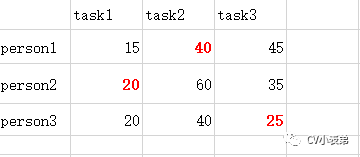
分配问题:假设有N个人N个任务,每个任务可以分配给任意不同的人,不同的人对不同的任务需要花费的代价也不相同,那么如何分配才能使花费总代价最少。假设现在有三个任务,三个人,每个人完成每个任务的代价矩阵如下(代价可以是时间或者金钱等):
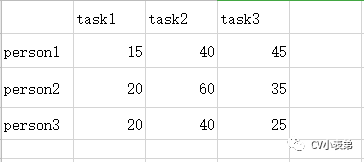
怎么才能找到一个分配方法使得任务花费代价最小呢?
匈牙利算法就是用来解决分配问题的一种方法,它基于理论:如果代价矩阵的某一行或某一列同时加或减某个数,则这个新的代价矩阵的最优分配任然是原代价矩阵的最优分配。
算法步骤(假设矩阵为NxN方阵):
1.对于矩阵的每一行,减去其中最小的元素
2.对于矩阵的每一列,减去其中最小的元素
3.用最少的水平线或垂直线覆盖矩阵中所有的0
4.如果线的数量等于N,则找到了最优分配,算法结束,否则进入步骤5
5.找到没有被任何线覆盖的最小元素,每个没被线覆盖的行减去这个元素,个被线覆盖的列加上这个元素,返回步骤3
继续拿上面的例子演示:
1.每一行减去其最小元素得到:

2.每一列减去其最小元素得到:
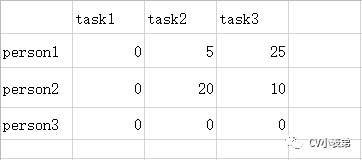
3.用最少的水平线或者垂直线覆盖所有的0得到:
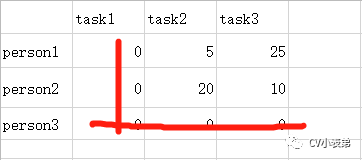
4.线的数量为2,小于3,进入第五步:
5.现在没被覆盖的最小元素是5,没被覆盖的行(第一和第二行)减去5,得到:

6.被覆盖的列(第一列)加上5,得到:
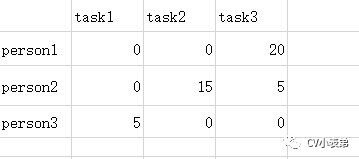
7.回到步骤3,用最少的线覆盖所有0:
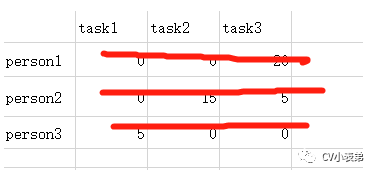
8.线的数量=3,算法结束,很显然,第一个任务给第二人,第二个任务给第一人,第三个任务给第三人,总代价最小(0+0+0):
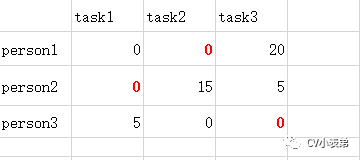
9.所以原矩阵最小代价为(40+20+25=85):