题目

标题和出处

标题：判断路径是否相交

出处：1496. 判断路径是否相交

难度

3 级

题目描述

要求

给你一个字符串 $\text{path}$，其中 $\text{path[i]}$ 的值可以是 $\text{‘N’}$、$\text{‘S’}$、$\text{‘E’}$ 或 $\text{‘W’}$，分别表示向北、向南、向东、向西移动一个单位。你从二维平面上的原点 $\text{(0, 0)}$ 处开始出发，按 $\text{path}$ 所指示的路径行走。

如果路径在任何位置上与自身相交，也就是走到之前已经走过的位置，请返回 $\text{true}$；否则，返回 $\text{false}$。

示例

示例 1：

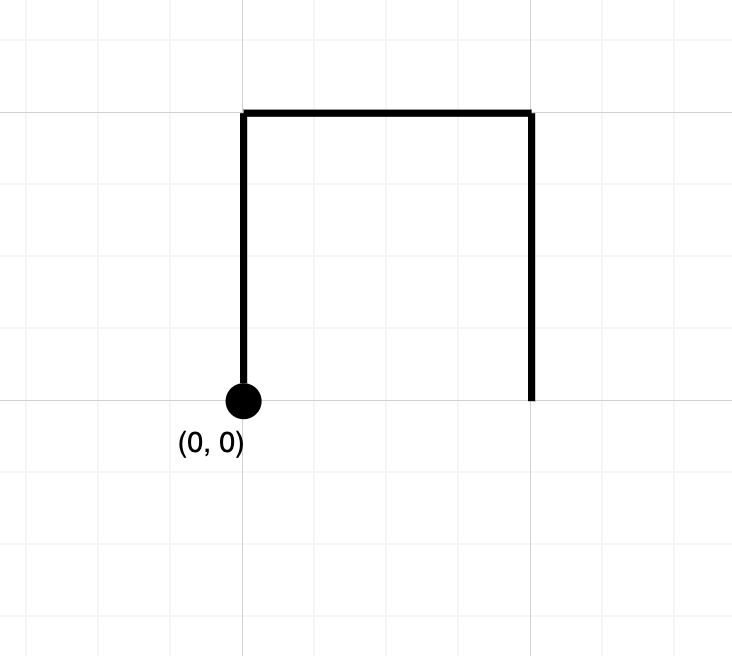
输入：$\text{path = "NES"}$
输出：$\text{false}$
解释：该路径没有在任何位置相交。

示例 2：

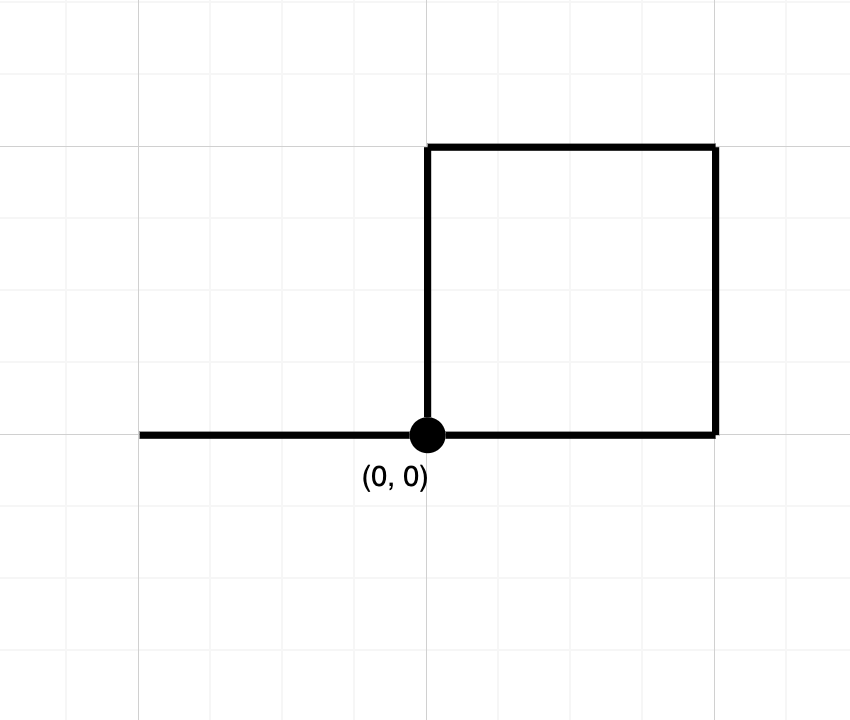
输入：$\text{path = "NESWW"}$
输出：$\text{true}$
解释：该路径经过原点两次。

数据范围

• $\text{1}\le \text{path.length}\le {\text{10}}^{\text{4}}$
• $\text{path[i]}$ 为 $\text{‘N’}$、$\text{‘S’}$、$\text{‘E’}$ 或 $\text{‘W’}$

解法一

思路和算法

判断路径是否相交，等价于判断是否存在到达超过一次的位置，可以使用哈希集合存储到达过的位置。

在二维平面内，每个位置由横坐标和纵坐标共同决定，哈希集合中的元素需要同时包含横坐标和纵坐标的信息。

一种做法是使用长度为 $2$ 的数组记录横坐标和纵坐标。由于数组本身不能判断是否重复，需要将数组转成字符串。

初始坐标是 $(0,0)$。将初始坐标加入哈希集合，然后遍历 $\text{path}$，对于每个字符，计算移动之后到达的坐标并加入哈希集合，如果存在一个到达的坐标已经在哈希集合中，则该坐标位置到达超过一次，路径相交，返回 $\text{true}$。如果遍历结束之后没有遇到同一个坐标位置到达超过一次，返回 $\text{false}$。

代码

class Solution {
    public boolean isPathCrossing(String path) {
        int x = 0, y = 0;
        Set<String> visited = new HashSet<String>();
        visited.add(Arrays.toString(new int[]{x, y}));
        int length = path.length();
        for (int i = 0; i < length; i++) {
            char c = path.charAt(i);
            switch (c) {
            case 'N':
                y++;
                break;
            case 'S':
                y--;
                break;
            case 'E':
                x++;
                break;
            case 'W':
                x--;
                break;
            }
            if (!visited.add(Arrays.toString(new int[]{x, y}))) {
                return true;
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是字符串 $\text{path}$ 的长度。需要遍历路径一次，对于每次移动需要计算到达的下标并加入哈希集合。这里假设存入哈希集合的字符串的长度是常数，哈希集合的每次操作的时间是 $O(1)$，实际运行时字符串在哈希集合中的操作所需时间和空间都较高。

• 空间复杂度：$O(n)$，其中 $n$ 是字符串 $\text{path}$ 的长度。需要使用哈希集合存储到达的下标，最多需要存储 $n+1$ 个下标。这里假设存入哈希集合的字符串的长度是常数，哈希集合的每次操作的时间是 $O(1)$，实际运行时字符串在哈希集合中的操作所需时间和空间都较高。

解法二

思路和算法

为了避免字符串操作，可以自定义哈希函数，将坐标转成整数。哈希函数应满足相同的坐标得到的哈希值相同，不同的坐标得到的哈希值不同。

由于 $\text{path}$ 的长度最大为 $10^4$，因此横坐标和纵坐标的取值范围都是 $[-10^4,10^4]$，各有 $20001$ 种可能的取值。可以定义哈希函数为 $f(x,y)=x\times 20001+y$，该哈希函数可以确保不同的坐标得到的哈希值不同。

假设存在整数坐标 $(x_1,y_1)$ 和 $(x_2,y_2)$ 满足 $f(x_1,y_1)=f(x_2,y_2)$，则有 $x_1\times 20001+y_1=x_2\times 20001+y_2$，即 $20001(x_1-x_2)=y_2-y_1$。由于 $|x_1-x_2|\le 20000$，$|y_2-y_1|\le 20000$，且坐标都是整数，因此一定有 $x_1-x_2=y_2-y_1=0$，$(x_1,y_1)$ 和 $(x_2,y_2)$ 是相同的坐标。

使用自定义哈希函数表示坐标，虽然时间复杂度和空间复杂度都与解法一相同（将解法一的哈希集合操作的时间和空间看成常数），但是实际运行时的性能会更好。

代码

class Solution {
    public boolean isPathCrossing(String path) {
        int x = 0, y = 0;
        Set<Integer> visited = new HashSet<Integer>();
        visited.add(getHash(x, y));
        int length = path.length();
        for (int i = 0; i < length; i++) {
            char c = path.charAt(i);
            switch (c) {
            case 'N':
                y++;
                break;
            case 'S':
                y--;
                break;
            case 'E':
                x++;
                break;
            case 'W':
                x--;
                break;
            }
            if (!visited.add(getHash(x, y))) {
                return true;
            }
        }
        return false;
    }

    public int getHash(int x, int y) {
        return x * 20001 + y;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是字符串 $\text{path}$ 的长度。需要遍历路径一次，对于每次移动需要计算到达的下标并加入哈希集合。

• 空间复杂度：$O(n)$，其中 $n$ 是字符串 $\text{path}$ 的长度。需要使用哈希集合存储到达的下标，最多需要存储 $n+1$ 个下标。