算法总结c++

news2024/9/21 13:34:37

文章目录

  • 基本概念
    • 时间复杂度
    • 空间复杂度
  • 基本结构
    • 1. 数组
      • 前缀和
      • 差分数组
      • 快慢指针(索引)
      • 左右指针（索引）
        • 盛水容器
        • 三数之和
        • 最长回文子串
    • 2. 链表
      • 双指针
        • 删除链表的倒数第 n 个结点
        • 翻转链表
      • 递归
        • 将两个升序链表合并为一个新的 升序 链表
        • 链表翻转
    • 3. 散列表
      • twoSum
      • 无重复的最长字符子串
    • 4. 栈stack
      • 回溯法解决组合问题
        • 电话号码字符组合
      • 括号匹配问题
        • 括号是否有效
    • 5. 队列queue
    • 6. 树
      • 深度优先遍历（前序遍历、中序遍历、后序遍历）
        • 翻转二叉树
      • 广度优先遍历（层序遍历）
        • 翻转二叉树
      • 递归
        • 树的深度
        • 对称二叉树
    • 7. 二叉堆
      • 优先队列
      • 堆排序
  • 经典算法
    • 1. 动态规划
      • 爬楼梯
      • 买卖股票

基本概念

时间复杂度

略

空间复杂度

略

基本结构

数组链表
读取O(1)O(n)
插入O(n)O(1)
删除O(n)O(1)

https://www.cnblogs.com/QG-whz/p/5152963.html#_label4_0

1. 数组

数组是一种线性数据结构，使用一组连续的内存空间存储一组具有相同类型的数据。

特性：

  1. 随机访问，即通过下标快速定位到数组中的元素，且时间复杂度是O(1)
  2. 插入数据和删除数据效率低
  3. 编译时预先申请内存空间，数组空间利用率低，不能动态拓展
  4. 在不够使用的时候需要扩容，涉及到需要把旧数组中的所有元素向新数组中搬移

题：

前缀和

计算并返回⼀个索引区间之内的元素和，适用于数组值固定

用 n + 1长数组记录前项和，

class NumArray {
    vector<int> presum;
public:
    NumArray(vector<int>& nums) {
        int n = nums.size();
        presum.resize(n + 1);
        presum[0] = 0;
        for(int i=1; i<=n; ++i){
            presum[i] = presum[i - 1] + nums[i - 1];
        }
    }
    
    int sumRange(int left, int right) {
        return presum[right + 1] - presum[left];
    }
};

https://leetcode.cn/problems/range-sum-query-immutable/
https://leetcode.cn/problems/range-sum-query-2d-immutable/

差分数组

数组长度固定，多次在区间内加相同常数，求最终数组。适用于变化前后区间内部元素差值不变的情况

// 差分数组⼯具类
class Difference {
 // 差分数组
	 private int[] diff;

 /* 输⼊⼀个初始数组，区间操作将在这个数组上进⾏ */
 public Difference(int[] nums) {
	 assert nums.length > 0;
	 diff = new int[nums.length];
	 // 根据初始数组构造差分数组
	 diff[0] = nums[0];
 	 for (int i = 1; i < nums.length; i++) {
		 diff[i] = nums[i] - nums[i - 1];
	 }
 }
 /* 给闭区间 [i, j] 增加 val（可以是负数）*/
 public void increment(int i, int j, int val) {
	 diff[i] += val;
 	 if (j + 1 < diff.length) {
		 diff[j + 1] -= val;
	 }
 }
 /* 返回结果数组 */
 public int[] result() {
	 int[] res = new int[diff.length];
	 // 根据差分数组构造结果数组
	 res[0] = diff[0];
	 for (int i = 1; i < diff.length; i++) {
		 res[i] = res[i - 1] + diff[i];
	 }
	 return res;
 }
}

构建与原数组等长的差分数组，处理区域变化时仅对头尾（+1）做加减，最终恢复正常数组时反向操作

https://leetcode.cn/problems/car-pooling/
https://leetcode.cn/problems/corporate-flight-bookings/

快慢指针(索引)

快慢指针解决有序数组的去重（快指针探路，慢指针填数）

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if(n < 2)return n;
        int slow = 0;
        for(int fast = 0; fast < n; ++fast){
            if(nums[slow] != nums[fast])      
                nums[++slow] = nums[fast]; 注意++i还是i++
        }
        return slow + 1;
    }
};

https://leetcode.cn/problems/remove-duplicates-from-sorted-array/comments/
https://leetcode.cn/problems/remove-element/submissions/
https://leetcode.cn/problems/move-zeroes/submissions/

左右指针（索引）

盛水容器

两个指针指向两头，由于短板效应，两条边的最短一条决定了面积，此时如果长边内移则面积一定减少，所以就让短边内移

int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int area = 0;
        while(left < right){
            area = height[left] < height[right] ? 
                    max(area, (right - left) * height[left++]): 
                    max(area, (right - left) * height[right--]);
        }
        return area;
    }

https://leetcode.cn/problems/container-with-most-water/

三数之和

给出数组中a + b + c = 0的全部情况（不能重复，ijk不相同）

先排序，然后可以遍历i（0~n-2），使用双指针，其中left=i+1，right=n-1，二者往内移动，注意跳过三个指针重复的情况，去掉ai > target的情况。

vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> anns;
        if(nums.empty() || nums.size() < 3)return anns;
        std::sort(nums.begin(), nums.end());
        for(int i = 0; i < nums.size() - 2; ++i){
            if(nums[i] > 0)return anns;
            if(i > 0 && nums[i] == nums[i - 1])continue;
            int left = i + 1;
            int right = nums.size() - 1;
            while(left < right){
                if(nums[i] + nums[left] + nums[right] == 0){
                    anns.push_back({nums[i], nums[left], nums[right]});
                    while(left < right && nums[left] == nums[left + 1])left++;
                    while(left < right && nums[right] == nums[right - 1])right--;
                    left++;
                    right--;
                }
                else if(nums[i] + nums[left] + nums[right] > 0){
                    right--;
                }
                else if(nums[i] + nums[left] + nums[right] < 0){
                    left++;
                }
            }
        }
    return anns;
    }

https://leetcode.cn/problems/3sum/submissions/

最长回文子串

回文串是中心对称的，只需要设置中心，用左右指针向两边扩散即可，当左右指针值相同时，就是回文，注意中心可以是一个元素，也可以是俩，遍历中心即可。

class Solution {
public:
    string longestPalindrome(string s) {
        for(int i = 0; i < s.size(); ++i){
            func(s, i, i);
            func(s, i, i + 1);
        }
        return s.substr(left, len);

    }
private:
    int left = 0;
    int right = 0;
    int len = 0;
    void func(string& s, int i, int j){
        while(i >= 0 && j < s.size() && s[i] == s[j]){
            if(j - i + 1 > len){
                len = j - i + 1;
                left = i;
            }
            i--;
            j++;
        }
    }
};

复杂度 O ( n 2 ) O(n^2) O(n2)

https://leetcode.cn/problems/longest-palindromic-substring/

2. 链表

链表，也是一种线性数据结构，为了保证链表中元素的连续性，一般使用一个指针来找到下一个元素。

特性：

  1. 任意位置插入元素和删除元素的速度快
  2. 内存利用率高，不会浪费内存
  3. 链表的空间大小不固定，可以动态拓展
  4. 随机访问效率低，时间复杂度为0(N)

链表主要分为以下几类：

  1. 单向链表，包含两个域，一个信息域和一个指针域。这个链接指向列表中的下一个节点，而最后一个节点则指向一个空值。
  2. 双向链表，也叫双链表，双向链表中不仅有指向后一个节点的指针，还有指向前一个节点的指针，这样可以从任何一个节点访问前一个节点，当然也可以访问后一个节点。
  3. 循环链表，中第一个节点之前就是最后一个节点，反之亦然。循环链表的无边界使得在这样的链表上设计算法会比普通链表更加容易。

双指针

删除链表的倒数第 n 个结点

前后指针差n位即可。

ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* tmp = new ListNode(0, head);
        ListNode* left = tmp;
        ListNode* right = head; 
        for(int i = 0; i < n; ++i){
            right = right->next;
        }
        while(right){
            right = right->next;
            left = left->next;
        }
        left->next = left->next->next;
        ListNode* ans = tmp->next;
        delete tmp;
        return ans;

    }

https://leetcode.cn/problems/remove-nth-node-from-end-of-list/

翻转链表

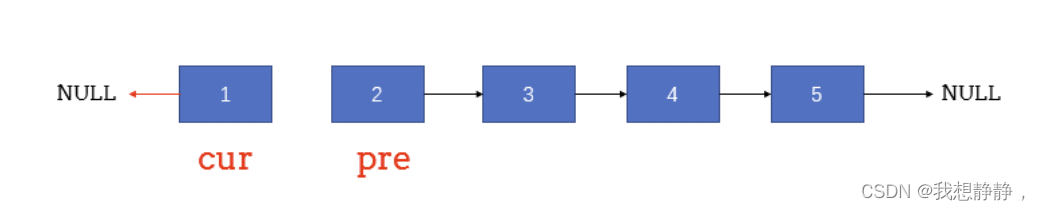
在这里插入图片描述
左指针指向null，右指针指向头，使用tmp指针记录右指针的下一个节点，让右指针指向左指针，然后左右指针右移，

ListNode* reverseList(ListNode* head) {
        ListNode* left = nullptr;
        ListNode* right = head;
        while(right){
            ListNode* tmp = right->next;
            right->next = left;
            left = right;
            right = tmp;
        }
        return left;
    }

https://leetcode.cn/problems/reverse-linked-list/

递归

递归函数必须要有终止条件，否则会出错；
递归函数先不断调用自身，直到遇到终止条件后进行回溯，最终返回答案。

将两个升序链表合并为一个新的 升序 链表

利用递归法，每次比较两个头节点的大小，并让小头->next指向后部分的结果

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(!list1)return list2;
        if(!list2)return list1;
        if(list1->val < list2->val){
            list1->next = mergeTwoLists(list1->next, list2);
            return list1;
        }
        else{
            list2->next = mergeTwoLists(list1, list2->next);
            return list2;
        }
    }

https://leetcode.cn/problems/merge-two-sorted-lists/

链表翻转

递归可以回溯

递归到最后的节点后返回，返回后，此时head是倒数第二个节点，令倒数第二个节点的next的next（最后一个节点）指向自己，然后让倒数第二个节点的next=null。

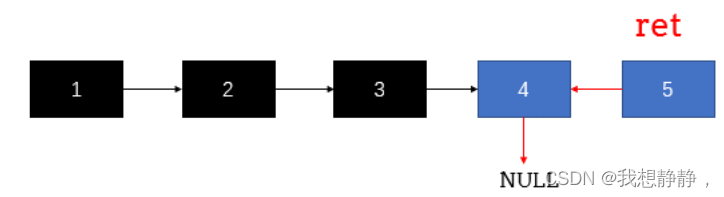
在这里插入图片描述

ListNode* reverseList(ListNode* head) {
        if(head == nullptr || head->next == nullptr)return head;
        auto newhead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newhead;
    }

https://leetcode.cn/problems/reverse-linked-list/

3. 散列表

散列表也叫作哈希表（hash table），这种数据结构提供了键（Key）和值（Value）的映射关系。只要给出一个Key，就可以高效查找到它所匹配的Value，时间复杂度接近于O(1)

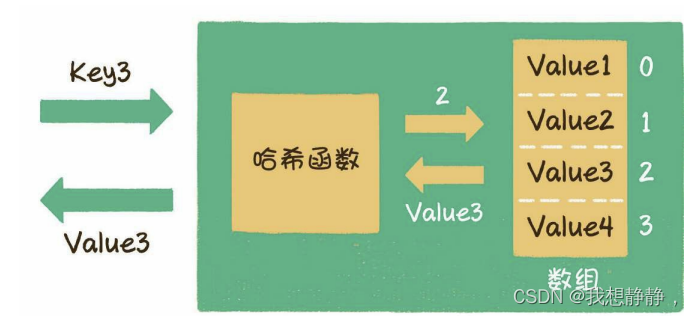
在这里插入图片描述
通过哈希函数，把Key和数组下标进行转换，即可实现快速查询。最简单的哈希函数是按照数组长度进行取模运算:
i n d e x = H a s h C o d e ( K e y ) % A r r a y . l e n g t h index = HashCode (Key) \% Array.length index=HashCode(Key)%Array.length

但存在哈希冲突，解决办法：

  1. 开放寻址法，即后移一位
  2. 链表法
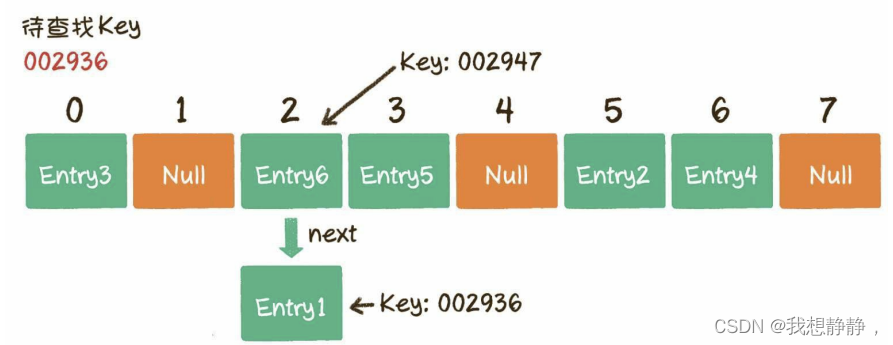
    在这里插入图片描述

当哈希冲突过多时，就需要扩容操作：
3. 当HashMap.Size 大于等于 HashMap的当前长度Capacity 乘以 HashMap的负载因子LoadFactor（默认值为0.75f），进行扩容。
4. 创建一个新的Entry空数组，长度是原数组的2倍。重新Hash，遍历原Entry数组，把所有的Entry重新Hash到新数组中。

twoSum

如果假设输入一个数组 nums 和一个目标和 target，请你返回 nums 中能够凑出 target 的两个元素的值，
使用hashtable记录nums[i]和i，然后遍历nums，查询target - nums[i]是否存在，复杂度O(n)

vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashtable;
        for(int i = 0; i < nums.size(); ++i){
            auto it = hashtable.find(target - nums[i]);
            if(it == hashtable.end()){
                hashtable[nums[i]] = i;
            }
            else{
                return {i, it->second};
            }
        }
        return {};
    }

https://leetcode.cn/problems/two-sum/

无重复的最长字符子串

滑窗法：用散列表或者unordered_set（可快速查询）存储字符是否出现，左指针右移一位，就把原值从unordered_set删除，然后右指针向右移动至出现重复字符。

int lengthOfLongestSubstring(string s) {
        unordered_set<char> contain;
        int right = -1; 
        int ans = 0;
        int n = s.size();
        for(int left = 0; left < n; ++left){
            if(left != 0){
                contain.erase(s[left - 1]);
            }
            while(right + 1 < n && !contain.count(s[right + 1])){
                contain.emplace(s[++right]);
            }
            ans = max(ans, right - left + 1);
        }
        return ans;

    }

时间复杂度O(n)

https://leetcode.cn/problems/longest-substring-without-repeating-characters/

4. 栈stack

  • 线性数据结构
  • 先入后出

栈最主要的功能就是回溯。

回溯法解决组合问题

电话号码字符组合

组合问题是经典需要回溯功能的问题，可以用栈实现。本题中使用递归来回溯号码，使用栈来配合

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        vector<string> ans;
        if(digits.size() == 0)return ans;
        unordered_map<char, string> phonemap{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };
        string combination;
        back(ans, combination, 0, digits, phonemap);
        return ans;
    }

    void back(vector<string>& ans, string& combination, int index, string& digits, unordered_map<char, string>& phonemap){
        if(index == digits.size()){
            ans.push_back(combination);
        }
        else{
            char x = digits[index];
            string strings = phonemap.at(x);
            for(auto& s: strings){
                combination.push_back(s);
                back(ans, combination, index + 1, digits, phonemap);
                combination.pop_back();
            }
        }
    }
};

https://leetcode.cn/problems/letter-combinations-of-a-phone-number/

括号匹配问题

括号是否有效

栈先进后出，正好符合括号匹配：

使用哈希map记录左右括号，左为key。左括号入栈，如果不是左括号，就判断是否是栈顶左括号对应的右括号。注意初始时就是右括号的情况，

bool isValid(string s) {
        int n = s.size();
        if(n % 2 == 1)return false;
        unordered_map<char, char> charmap({{'(', ')'},
                                            {'{', '}'},
                                            {'[', ']'}});
        stack<char> stk;
        for(auto& c: s){
            if(charmap.count(c)){
                stk.push(c);
            }
            else if(stk.empty() || c != charmap[stk.top()]){ //注意初始时就是右括号的情况 stk.empty()
                return false;
            }
            else{
                stk.pop();
            }
        }
        return stk.empty();

    }

https://leetcode.cn/problems/valid-parentheses/

5. 队列queue

  • 线性数据结构
  • 先入先出
  • 队列的出口端叫作队头（front），队列的入口端叫作队尾

6. 树

满二叉树要求所有分支都是满的；
而完全二叉树只需保证最后一个节点之前的节点都齐全即可，即满二叉树的部分

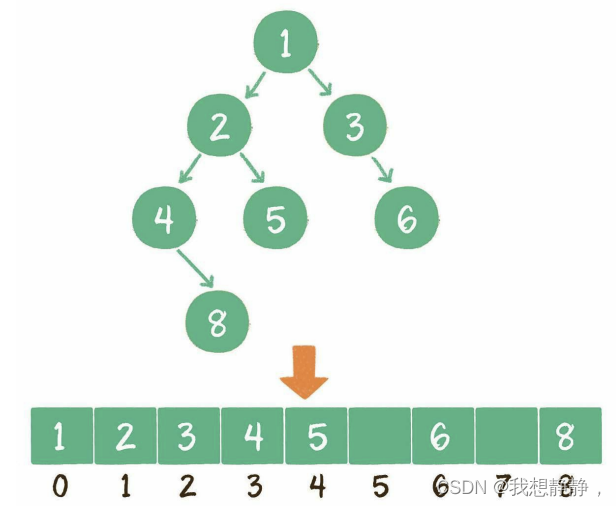
存储方式：

  1. 链表
  2. 数组，注意数组是按满二叉树的位置存放，缺失的节点就空出来，假设一个父节点的下标是parent，那么它的左孩子节点下标就是2×parent +1；右孩子节点下标就是2×parent + 2

在这里插入图片描述
二叉查找树（二叉排序树）： 如果左子树不为空，则左子树上所有节点的值均小于根节点的值，如果右子树不为空，则右子树上所有节点的值均大于根节点的值， 左、右子树也都是二叉查找树。

当所有节点的值是有序时，二叉查找树就退化了，此时需要二叉树的自平衡了。二叉树自平衡的方式有多种，如红黑树、AVL树、树堆等

深度优先遍历（前序遍历、中序遍历、后序遍历）

  1. 递归
  2. 非递归，使用栈

####中序遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        func(root, ans);
        return ans;
    }
    void func(TreeNode* root, vector<int>& ans){
        if(!root)return;
        func(root->left, ans);
        ans.push_back(root->val);
        func(root->right, ans);
    }
};

https://leetcode.cn/problems/binary-tree-inorder-traversal/

翻转二叉树

TreeNode* invertTree(TreeNode* root) {
        if(!root)return root;
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;   
        return root;
    }

https://leetcode.cn/problems/invert-binary-tree/

广度优先遍历（层序遍历）

使用队列，令出队节点的左右子节点分别入队即可。

翻转二叉树

TreeNode* invertTree(TreeNode* root) {
        if(!root)return root;
        queue<TreeNode*> Que;
        Que.push(root);
        while(!Que.empty()){
            auto t = Que.front();
            Que.pop();
            auto tmp = t->left;
            t->left = t->right;
            t->right = tmp;
            if(t->left)Que.push(t->left);
            if(t->right)Que.push(t->right);
        }
        return root;
    }

https://leetcode.cn/problems/invert-binary-tree/

递归

树的深度

左右子树的最大深度 + 1 = root的深度

int maxDepth(TreeNode* root) {
        if(!root)return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;

    }

https://leetcode.cn/problems/maximum-depth-of-binary-tree/

对称二叉树

比较根节点的左右值是否相同，如果相同，进一步比较左的左和右的右是否相同，以及左的右和右的左是否相同。

bool isSymmetric(TreeNode* root) {
        if(!root)return true;
        return func(root->left, root->right);
    }
    bool func(TreeNode* left, TreeNode* right){
        if(!left && !right)return true;
        if(!left || !right)return false;
        if(left->val != right->val){
            return false;
        }
        return func(left->left, right->right) && func(left->right, right->left);
    }

https://leetcode.cn/problems/symmetric-tree/

7. 二叉堆

二叉堆本质上是一种完全二叉树，二叉堆的所有节点都存储在数组中，分为两个类型。

最大堆的任何一个父节点的值，都大于或等于它左、右孩子节点的值
最小堆的任何一个父节点的值，都小于或等于它左、右孩子节点的值

二叉堆的根节点叫作堆顶。最大堆和最小堆的特点决定了：最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

插入节点：新节点插在最后，然后与父节点比较大小，进行上浮，逐级进行上述操作。
删除根节点：最后一个节点补上，然后与子节点比较，逐级下沉
把一个无序的完全二叉树调整为二叉堆：从最后一个非叶子节点开始，将所有非叶子节点与其子节点对比并下沉。

堆的插入和删除操作，时间复杂度是O(logn)。但构建堆的时间复杂度是O(n)。

二叉堆是实现堆排序及优先队列的基础

优先队列

优先队列不遵循先入先出的原则，而是分为两种情况。
最大优先队列，无论入队顺序如何，都是当前最大的元素优先出队
最小优先队列，无论入队顺序如何，都是当前最小的元素优先出队

优先队列入队和出队的时间复杂度也是O(logn)

以用最大堆来实现最大优先队列，每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点

堆排序

把无序数组构建成二叉堆。需要从小到大排序，则构建成最大堆；需要从大到小排序，则构建成最小堆。

循环删除堆顶元素，替换到二叉堆的末尾，调整堆产生新的堆顶。最终的数组就是排序结果。

整体的时间复杂度是O(nlogn)

经典算法

1. 动态规划

  • 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决

爬楼梯

设爬x层楼，有方法f(x)个，则f(x) = f(x-1) + f(x-2)，因为每次只能爬 1 级或 2 级

int climbStairs(int n) {
        int dp[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; ++i){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

https://leetcode.cn/problems/climbing-stairs/

买卖股票

遍历卖出的天，最大利润就是在卖出天前的最低价格。

int maxProfit(vector<int>& prices) {
        int minprice = 1e6;
        int ans = 0;
        for(int i = 0; i < prices.size(); i++){
            ans = max(ans, prices[i] - minprice);
            minprice = min(prices[i], minprice);
        }
        return ans;
    }

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/343217.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Camtasia2023最新版本新功能及快捷键教程

Camtasia2023最新版本新功能及快捷键教程

使用Camtasia&#xff0c;您可以毫不费力地在计算机的显示器上录制专业的活动视频。除了录制视频外&#xff0c;Camtasia还允许您从外部源将高清视频导入到录制中。Camtasia的独特之处在于它可以创建包含可单击链接的交互式视频&#xff0c;以生成适用于教室或工作场所的动态视…
阅读更多...
UDS诊断之DTC码构成

UDS诊断之DTC码构成

DTC(Diagnostic Trouble Code)表示诊断故障码&#xff08;全局唯一&#xff09;&#xff0c;是故障类型的"身份ID"&#xff1b;用于汽车故障时对故障部位及原因的排查。 格式如下&#xff1a; 其中&#xff0c;DTCHighByte、DTCMiddleByte这两个字节表示故障内码&…
阅读更多...
nvm控制node版本

nvm控制node版本

安装 nvm 1、下载 nvm 官网安装包&#xff1a; github 选择 nvm-setup.exe 下载 2、安装 1、选择 nvm 安装目录&#xff08;可自定义&#xff09; 2、选择 node 安装目录&#xff08;如有安装过&#xff0c;可以选择以前安装目录&#xff0c;可 cdm 输入 where node 查看原nod…
阅读更多...
嵌入式Qt 开发一个音乐播放器

嵌入式Qt 开发一个音乐播放器

上篇文章&#xff1a;RK3568源码编译与交叉编译环境搭建&#xff0c;进行了OK3568开发板软件开发环境搭建&#xff0c;通过编译RK3568的源码&#xff0c;可以得到Qt开发的交叉编译相关工具。 本篇&#xff0c;就来在搭建好的软件开发中&#xff0c;进行Qt软件的开发测试。由于…
阅读更多...
package-lock.json，深度内容

package-lock.json，深度内容

前言 看完本文&#xff0c;你将从整体了解依赖版本锁定原理&#xff0c;package-lock.json 或 yarn.lock 的重要性。首先要从最近接连出现两起有关 npm 安装 package.json 中依赖包&#xff0c;由于依赖包版本更新 bug 造成项目出错问题说起。 事件一&#xff1a;新版本依赖包…
阅读更多...
JavaScript 二叉树

JavaScript 二叉树

文章目录前言一、何为 树1.根节点2.外&内部节点3.子树4.深度5.高度二、二叉树 & 二叉搜索树1.二叉搜索树插入值2.遍历二叉搜索树I.中序遍历II.先序遍历III.后序遍历3.查找节点4.移除节点总结前言 同前面说到的散列表结构, 树也是一种非顺序数据结构, 对于存储需要快速…
阅读更多...
【浅学Nginx】Nginx安装和基础使用

【浅学Nginx】Nginx安装和基础使用

Nginx安装和基础使用1. Nginx是什么2. Nginx的安装3. Nginx的目录结构4. Nginx的配置文件结构5. Nginx的具体应用5.1 部署静态资源5.2 反向代理5.3 负载均衡1. Nginx是什么 Nginx是一个轻量级的 web服务器 / 反向代理服务器及电子邮件&#xff08;IMAP/POP3&#xff09;代理服…
阅读更多...
kettle开发-Day37-SQ索引优化

kettle开发-Day37-SQ索引优化

前言&#xff1a;在上一个生产项目中&#xff0c;有个单表数据超249G了&#xff0c;里面存储的数据时间跨度就1年左右&#xff0c;那为啥会出现这种情况呢&#xff1f;数据来源为&#xff0c;一个生产基地所有电表的每分钟读数&#xff0c;一个基地大概500个电表左右&#xff0…
阅读更多...
【C++】---Stack和Queue的用法及其模拟实现

【C++】---Stack和Queue的用法及其模拟实现

文章目录Stack最小栈栈的弹出压入序列逆波兰表达式求值用栈实现队列模拟实现queue用队列实现栈模拟实现Stack stack是一种容器适配器&#xff0c;专门用在具有后进先出操作的上下文环境中&#xff0c;其删除只能从容器的一端进行元素的插入与提取操作。它的使用和之前学习的ve…
阅读更多...
KDZD880 智能蓄电池放电测试仪

KDZD880 智能蓄电池放电测试仪

一、产品概述 智能蓄电池放电测试仪主要用于电信、移动、联通、电力直流行业的后备电源铅酸蓄电池的放电测试&#xff0c;具备蓄电池快速容量测试、在线监测及容量核对测试三大功能于一体的产品&#xff0c;集成化程度高、体积小巧、功能完善。 该设备是针对整组 12V-600V 蓄…
阅读更多...
JavaScript高级程序设计读书分享之3章——3.4数据类型

JavaScript高级程序设计读书分享之3章——3.4数据类型

JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 ECMAScript 有 6 种简单数据类型&#xff08;也称为原始类型&#xff09;&#xff1a;Undefined、Null、Boolean、Number、String 和 Symbol&#xff08;es6新增&#xff09;。 还有一种复杂数据类型叫…
阅读更多...
vim编辑器和gcc/g++编译器和gdb调试器和make/makefile自动化构建工具的使用

vim编辑器和gcc/g++编译器和gdb调试器和make/makefile自动化构建工具的使用

vim的三种模式(其实有好多模式 )&#xff08;1&#xff09;.命令模式&#xff08;2&#xff09;.插入模式&#xff08;3&#xff09;.底行模式vim的基本操作vim的命令模式的基本操作vim的插入模式的基本操作vim的底行模式的基本操作vim的配置gcc和g相关操作&#xff08;1&#…
阅读更多...
XCP实战系列介绍11-几个常用的XCP命令解析

XCP实战系列介绍11-几个常用的XCP命令解析

本文框架 1.概述2. 常用命令解析2.1 CONNECT连接(0xFF)2.2 SHORT_UPLOAD 命令(0xF4)2.2 SET_MTA (0xF6)2.3 MOVE命令(0x19)2.4 GET_CAL_PAGE(0xEA)2.5 SET_CAL_PAGE(0xEB)2.6 DOWNLOAD(0xF0)1.概述 在文章《看了就会的XCP协议介绍》中详细介绍了XCP的协议，在《XCP实战系列介绍…
阅读更多...
Python面试——装饰器

Python面试——装饰器

知识链接&#xff1a; 装饰器 装饰器可调用的对象&#xff0c;其参数是被装饰的函数。装饰器可能会处理被装饰的函数然后把它返回&#xff0c;或者将其替换成另外一个函数或者可调用对象。 装饰器有两大特性&#xff1a; 能把被装饰的函数替换成其他函数&#xff08;在元编程…
阅读更多...
面试腾讯测试岗后感想，真的很后悔这5年一直都干的是基础测试....

面试腾讯测试岗后感想，真的很后悔这5年一直都干的是基础测试....

前两天&#xff0c;我的一个朋友去大厂面试&#xff0c;跟我聊天时说&#xff1a;输的很彻底… 我问她&#xff1a;什么情况&#xff1f;她说&#xff1a;很后悔这5年来一直都干的是功能测试… 相信许多测试人也跟我朋友一样&#xff0c;从事了软件测试很多年&#xff0c;却依…
阅读更多...
树莓派用默认账号和密码登录不上怎么办；修改树莓派的密码

树莓派用默认账号和密码登录不上怎么办；修改树莓派的密码

目录 一、重置树莓派的默认账号和密码 二、修改树莓派的密码 三、超级用户和普通用户的切换 一、重置树莓派的默认账号和密码 在SD卡中根目录建立文件userconf 在userconf中输入如下内容&#xff1a; pi:$6$/4.VdYgDm7RJ0qM1$FwXCeQgDKkqrOU3RIRuDSKpauAbBvP11msq9X58c8Q…
阅读更多...
STM32开发（10）----CubeMX配置基本定时器

STM32开发（10）----CubeMX配置基本定时器

CubeMX配置基本定时器前言一、定时器的介绍二、实验过程1.实验材料2.STM32CubeMX配置基本定时器2.代码实现3.编译烧录4.硬件连接5.实验结果总结前言 本章介绍使用STM32CubeMX对基本定时器进行配置的方法&#xff0c;STM32F103高性能系列设备包括基本定时器、高级控制定时器、通…
阅读更多...
JavaEE-HTTP协议(一)

JavaEE-HTTP协议(一)

目录什么是HTTP协议&#xff1f;协议格式如何看到HTTP的报文格式&#xff1f;HTTP请求HTTP响应URLURL encode/decode什么是HTTP协议&#xff1f; 计算机网络&#xff0c;核心概念&#xff0c;网络协议 网络协议种类非常多&#xff0c;其中一些耳熟能详的&#xff0c;IP,TCP,UD…
阅读更多...
shell命令行并行神器 - parallel

shell命令行并行神器 - parallel

shell命令行并行神奇 - parallel 概述 GNU parallel 是一个 shell 工具&#xff0c;用于使用一台或多台计算机并行执行作业。作业可以是单个命令或必须为输入中的每一行运行的小脚本。典型的输入是文件列表、主机列表、用户列表、URL 列表或表列表。作业也可以是从管道读取的…
阅读更多...
98年的确实卷，公司新来的卷王，我们这帮老油条真干不过.....

98年的确实卷，公司新来的卷王，我们这帮老油条真干不过.....

都说00后躺平了&#xff0c;但是有一说一&#xff0c;该卷的还是卷。这不&#xff0c;前段时间我们公司来了个00后&#xff0c;工作没两年&#xff0c;跳槽到我们公司起薪18K&#xff0c;都快接近我了。后来才知道人家是个卷王&#xff0c;从早干到晚就差搬张床到工位睡觉了。 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023