文章目录
- 问题引入
- 关于权重
- 权重共享
- RNN Cell
- RNN原理
- RNN计算过程
- 代码实现
- RNN Cell
- 维度说明
- 代码
- RNN
- 维度说明
- NumLayers
- 说明
- 计算过程
- 代码
- 参考实例
- 问题分析
- 多分类问题
- 代码
- RNN Cell
- RNN
- 改进
- Embedding
- 网络结构
- Embedding说明
- Linear说明
- 代码
课程来源: 链接
课程文本参考:Birandaの
问题引入
在前篇中所提到的线性网络,大致上都是稠密网络(DNN)这种网络的输入大多是样本的多维度的特征,以此来得到一个想要的输出。
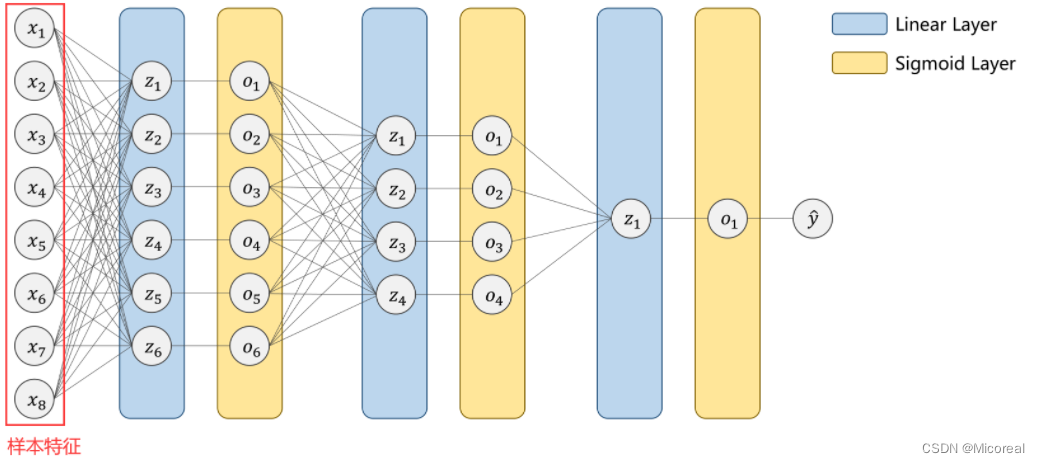
显然,面对序列问题,即处理视频流、预测天气、自然语言等等问题时,此时输入的
x
1
⋯
x
n
x_1 \cdots x_n
x1⋯xn实际上是一组有序列性即存在前后关系的样本。每个
x
i
x_i
xi为一个样本的所包含的特征元组。
针对这样的问题,我们也会想到利用线性的全连接网络来进行处理,但事实上,全连接网络所需要计算的权重太多,并不能够解决问题。
关于权重
对于一张128通道的图片,若想要利用
5
×
5
5 \times 5
5×5的卷积核将它转换成一张64通道的图片,则需要计算的权重有大约20W个
128
×
5
2
×
64
=
204800
128 \times 5^2 \times 64 = 204800
128×52×64=204800
即卷积层的权重数目只与通道数以及卷积核大小有关,但全连接层的权重数与转成一维向量以后的整个数据量有关
若转为一维向量以后,输入为4096个元素,输出为1024个元素,则需要计算的权重大约有400W个
4096
×
1024
=
4194304
4096 \times 1024 = 4194304
4096×1024=4194304
显然,全连接层所需要计算的权重远多于卷积层
权重共享
给定一张输入图片,用一个固定大小的卷积核去对图片进行处理,卷积核内的参数即为权重,而卷积核是对输入图片进行步长为stride的扫描计算,也就是说原图中的每一个像素都会参与到卷积计算中,因此,对于整个卷积核而言,权重都是一样的,即共享。
权重共享,实际上是计划通过将输入图片的一个局部特征映射成输出图片的一个像素点而发挥作用的,也就是通过卷积核,使得输出层的每一个像素只与输入层一个局部的方块相连接,这就避免了在全连接情形下的,输出层的每个像素都在或多或少的被输入层的任意一个像素影响这一复杂的情况。
另外,图像信息的特征:图片底层特征与特征在图片中的位置无关,也是权重共享的一个依据。例如对于图像的边缘特征,无论边缘处在图像的什么位置,都是以同样的方法定义,作为同样的特征进行区别的。
因此,为了能够较好地解决序列问题,也要利用到权重共享的思路方法,来减少在计算过程中所需要的权重。因此产生了RNN
RNN Cell
RNN原理
| 模块名称 | 作用 |
|---|---|
| x t x_t xt | 表时刻 t t t时的输入数据 |
| RNN Cell | 本质上是一个线性层 |
| h t h_t ht | 表时刻 t t t时得到的输出(隐含层) |
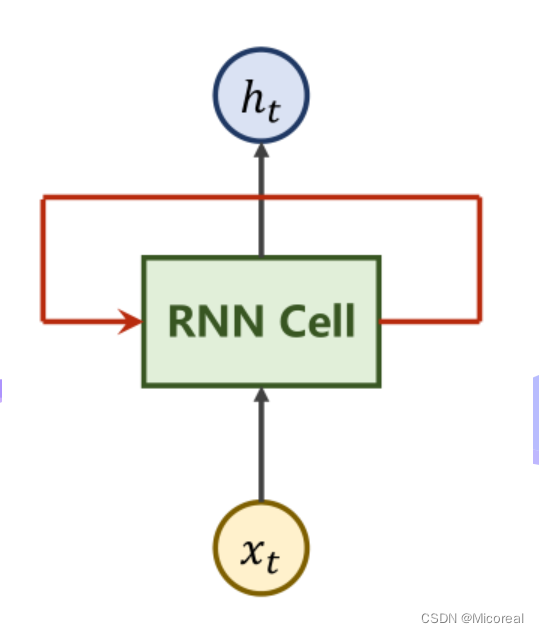
本质上,RNN Cell为一个线性层Linear,在
t
t
t时刻下的
N
N
N维向量,经过Cell后即可变为一个
M
M
M维的向量
h
t
h_t
ht,而与其他线性层不同,RNN Cell为一个共享的线性层。即重复利用,权重共享。将上图展开来看如下。
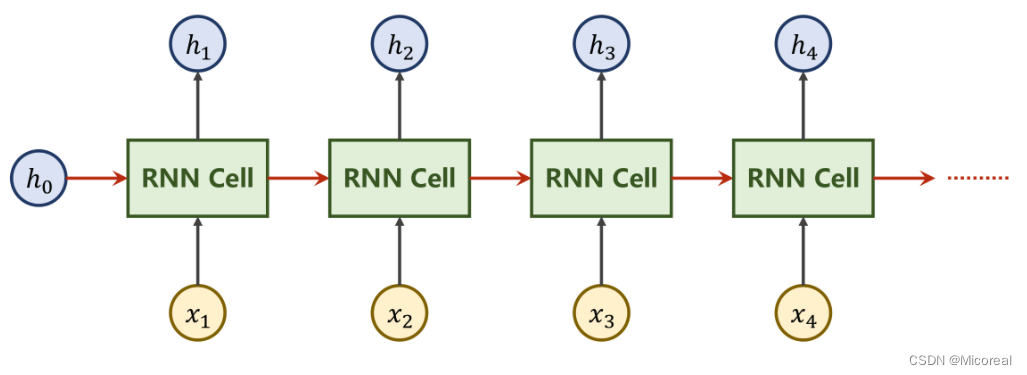
由于
x
1
⋯
x
n
x_1 \cdots x_n
x1⋯xn,为一组序列信息,每一个
x
i
x_i
xi都至少应包含
x
i
−
1
x_{i-1}
xi−1的信息。也就是说,针对
x
2
x_2
x2的操作所得到的
h
2
h_2
h2中,应当包含
x
1
x_1
x1的信息,因此在设计中,把
x
1
x_1
x1处理后得到的
h
1
h_1
h1一并向下传递。
上图中的
h
0
h_0
h0是一种前置信息。例如若实现图像到文本的转换,可以利用CNN+FC对图像进行操作,再将输出的向量作为
h
0
h_0
h0参与到RNN的运算中。
若没有可获知的前置信息,可将
h
0
h_0
h0设置为与
x
i
x_i
xi同维度的零向量。
图中的RNN Cell为同一个Linear,即让设计好的Linear反复参与运算,实现权重共享。
RNN计算过程
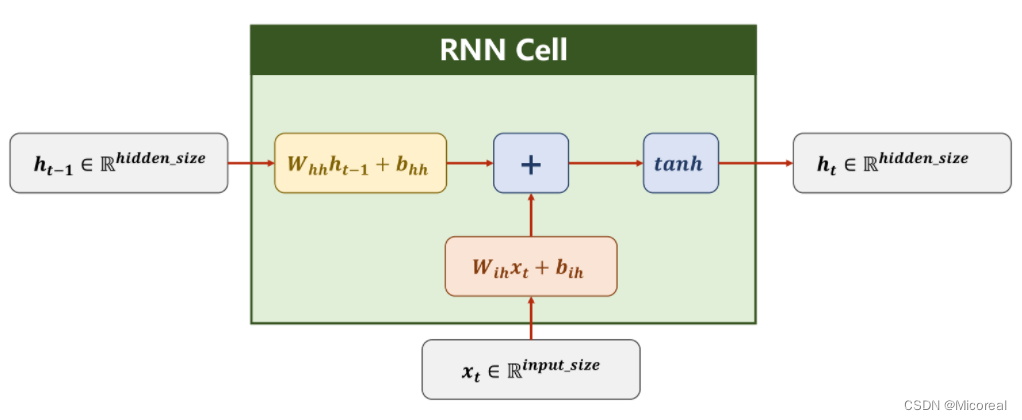
对上图中的符号做出解释如下
| 符号 | 标注 |
|---|---|
| h t h_t ht h t − 1 h_{t-1} ht−1 | 隐藏层hidden的结果向量 |
| x t x_t xt | 输入层的输入向量 |
| R h i d d e n _ s i z e R ^{hidden\_size} Rhidden_size | 表隐藏层的向量维度 |
| R i n p u t _ s i z e R^{input\_size} Rinput_size | 表输入层的向量维度 |
| W i h W_{ih} Wih | 用于计算输入的权重,维度大小为 h i d d e n _ s i z e × i n p u t _ s i z e hidden\_size \times input\_size hidden_size×input_size |
| b i h b_{ih} bih | 用于计算输入时的偏置量 |
| W h h W_{hh} Whh | 用于计算隐藏层的权重,维度大小为 h i d d e n _ s i z e × h i d d e n _ s i z e hidden\_size \times hidden\_size hidden_size×hidden_size |
| b h h b_{hh} bhh | 用于计算隐藏层时的偏置量 |
| tanh | 激活函数,值域为 ( − 1 , + 1 ) (-1, +1) (−1,+1) |
| + | 求和模块 |
在RNN计算过程中,分别对输入
x
t
x_t
xt以及前文的隐藏层输出
h
t
−
1
h_{t-1}
ht−1进行线性计算,再进行求和,对所得到的一维向量,利用tanh激活函数进行激活,由此可以得到当前隐藏层的输出
h
t
h_t
ht,其计算过程如下:
h
t
=
t
a
n
h
(
W
i
h
x
t
+
b
i
h
+
W
h
h
h
t
−
1
+
b
h
h
)
h_t = tanh(W_{ih}x_t + b_{ih} + W_{hh}h_{t-1} + b_{hh})
ht=tanh(Wihxt+bih+Whhht−1+bhh)
实际上,在框中的RNN Cell,的计算过程中为线性计算。
W
h
h
h
t
−
1
+
W
i
h
x
t
=
[
W
h
h
W
i
h
]
[
h
x
]
W_{hh}h_{t-1}+W_{ih}x_{t} = \begin{bmatrix} {W_{hh}}&{W_{ih}} \end{bmatrix} \begin{bmatrix} h\\ x \end{bmatrix}
Whhht−1+Wihxt=[WhhWih][hx]
即在实际运算的过程中,这两部分是拼接到一起形成矩阵再计算求和的,最终形成一个大小为
h
i
d
d
e
n
_
s
i
z
e
×
1
hidden\_size \times 1
hidden_size×1的张量。
代码实现
代码实现有两种模式,一是实现自己的RNN Cell,再自己重写循环调用等逻辑。二是直接调用RNN的网络。
重点在于控制其输入输出的维度。
RNN Cell
#输入维度input_size,隐藏层维度hidden_size
cell = torch.nn.RNNCell(input_size = input_size, hidden_size = hidden_size)
#输入的input 的维度(B*input_size), hidden的维度(B*hidden_size)
#输出的hidden维度(B*hidden_szie)
hidden = cell(input, hidden)
维度说明
为说明输入输出维度大小,假定当前有如下配置的数据
| 参数 | 值 | 说明 |
|---|---|---|
| BatchSize | 1 | 批量大小 |
| SeqLen | 3 | 样本数目 x 1 x_1 x1 x 2 x_2 x2 x 3 x_3 x3 |
| InputSize | 4 | 输入维度 |
| HiddenSize | 2 | 隐藏层(输出)维度 |
对于RNN Cell而言在hidden = cell(input, hidden)中
| 参数 | 值 | 说明 |
|---|---|---|
| input | ([1, 4]) | i n p u t . s h a p e = ( b a t c h _ s i z e , i n p u t _ s i z e ) input.shape = (batch\_size, input\_size) input.shape=(batch_size,input_size) |
| hidden | ([1, 2]) | o u t p u t . s h a p e = ( b a t c h _ s i z e , h i d d e n _ s i z e ) output.shape = (batch\_size, hidden\_size) output.shape=(batch_size,hidden_size) |
而整个数据集的维度应为
d
a
t
a
s
e
t
.
s
h
a
p
e
=
(
s
e
q
L
e
n
,
b
a
t
c
h
_
s
i
z
e
,
i
n
p
u
t
_
s
i
z
e
)
dataset.shape = (seqLen, batch\_size, input\_size)
dataset.shape=(seqLen,batch_size,input_size)
代码
import torch
batch_size = 1
seq_len = 3
input_size = 4
hidden_size =2
cell = torch.nn.RNNCell(input_size = input_size, hidden_size = hidden_size)
#维度最重要
dataset = torch.randn(seq_len,batch_size,input_size)
#初始化时设为零向量
hidden = torch.zeros(batch_size, hidden_size)
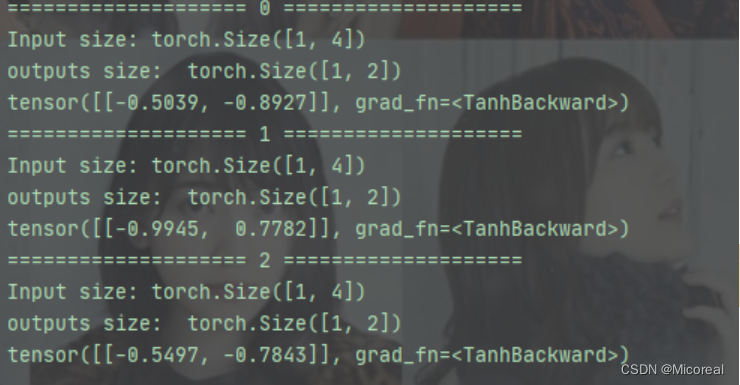
for idx,input in enumerate(dataset):
print('=' * 20,idx,'=' * 20)
print('Input size:', input.shape)
hidden = cell(input, hidden)
print('outputs size: ', hidden.shape)
print(hidden)
RNN
#说明input维度,hidden维度,以及RNN层数
#RNN计算耗时大,不建议层数过深
cell = torch.nn.RNN(input_size = input_size, hidden_size = hidden_size, num_layers = num_layers)
#inputs指的是X1……Xn的整个输入序列
#hidden指的是前置条件H0
#out指的是每一次迭代的H1……Hn隐藏层序列
#hidden_out指的是最后一次迭代得到输出Hn
out, hidden_out = cell(inputs, hidden)
维度说明
为说明输入输出维度大小,假定当前有如下配置的数据
| 参数 | 值 | 说明 |
|---|---|---|
| BatchSize | 1 | 批量大小 |
| SeqLen | 5 | 样本数目 x 1 x_1 x1 x 2 x_2 x2 x 3 x_3 x3 x 4 x_4 x4 x 5 x_5 x5 |
| InputSize | 4 | 输入维度 |
| HiddenSize | 2 | 隐藏层(输出)维度 |
| numLayers | 3 | RNN层数 |
对于RNN而言,在out, hidden_out = cell(inputs, hidden)
| 参数 | 值 | 说明 |
|---|---|---|
| input | ([5, 1, 4]) | i n p u t . s h a p e = ( s e q L e n , b a t c h _ s i z e , i n p u t _ s i z e ) input.shape = (seqLen, batch\_size, input\_size) input.shape=(seqLen,batch_size,input_size) |
| hidden | ([3, 1, 2]) | h i d d e n . s h a p e = ( n u m L a y e r s , b a t c h _ s i z e , h i d d e n _ s i z e ) hidden.shape = (numLayers, batch\_size,hidden\_size) hidden.shape=(numLayers,batch_size,hidden_size) |
| out | ([5, 1, 2]) | o u t . s h a p e = ( s e q L e n , b a t c h _ s i z e , h i d d e n _ s i z e ) out.shape = (seqLen, batch\_size,hidden\_size) out.shape=(seqLen,batch_size,hidden_size) |
| hidden_out | ([3, 1, 2]) | h i d d e n _ o u t . s h a p e = ( n u m L a y e r s , b a t c h _ s i z e , h i d d e n _ s i z e ) hidden\_out.shape = (numLayers, batch\_size,hidden\_size) hidden_out.shape=(numLayers,batch_size,hidden_size) |
NumLayers
说明
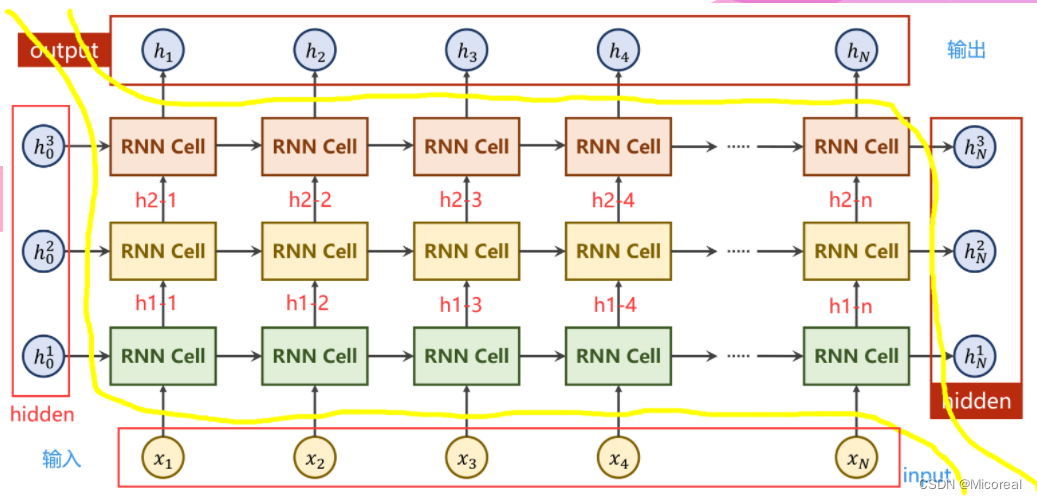
其中,左侧及下侧为输入部分,右侧及上侧为输出部分。
左侧是每一层RNN的前置条件,下侧为输入序列。右侧为每一层的隐藏层最终输出,上侧为隐藏层输出序列。
计算过程
在输入序列中的第
j
j
j个样本经过第
i
i
i层RNN Cell计算过后,所产生的隐藏层输出记为
h
j
i
h^i_j
hji,该输出分别向更深层的Cell即
i
+
1
i+1
i+1层RNN Cell,以及更靠后的序列即第
j
+
1
j+1
j+1个样本进行传递。
若
i
i
i为最后一层,则作为该样本的最终结果out_put输出。否则将继续向第
i
+
1
i+1
i+1层RNN传递。
若
j
j
j为序列中最后一个样本,则作为本层RNN的隐藏层最终结果hidden_out输出。否则将继续向第
j
+
1
j+1
j+1个样本传递。
图示是一张展开图,实际上,每一层的RNN Cell是同一个网络,以此来实现权重共享。
代码
import torch
batch_size = 1
seq_len = 5
input_size = 4
hidden_size =2
num_layers = 3
#其他参数
#batch_first=True 维度从(SeqLen*Batch*input_size)变为(Batch*SeqLen*input_size)
cell = torch.nn.RNN(input_size = input_size, hidden_size = hidden_size, num_layers = num_layers)
inputs = torch.randn(seq_len, batch_size, input_size)
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print("Output size: ", out.shape)
print("Output: ", out)
print("Hidden size: ", hidden.shape)
print("Hidden: ", hidden)
输出结果:
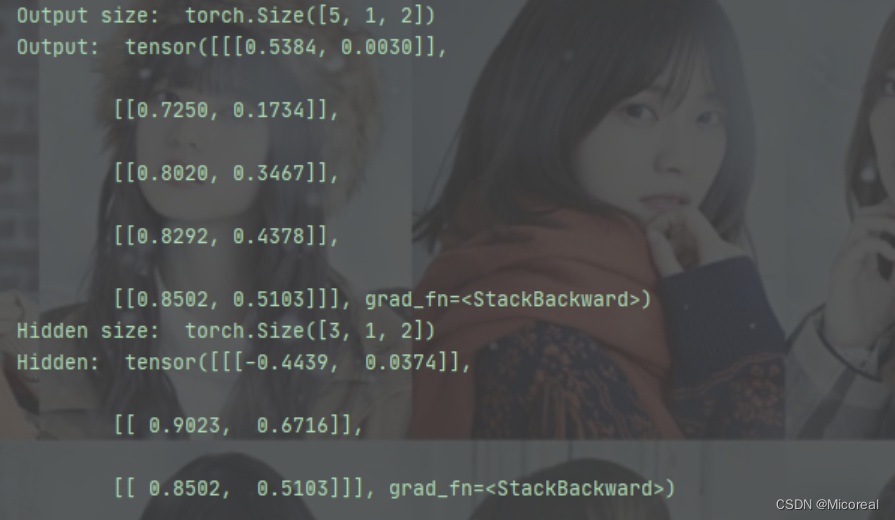
参考实例
假定现在有一个序列到序列 ( s e q → s e q ) (seq \to seq) (seq→seq)的任务,比如将“hello”转换为“ohlol”。
即利用RNN实现如下输出
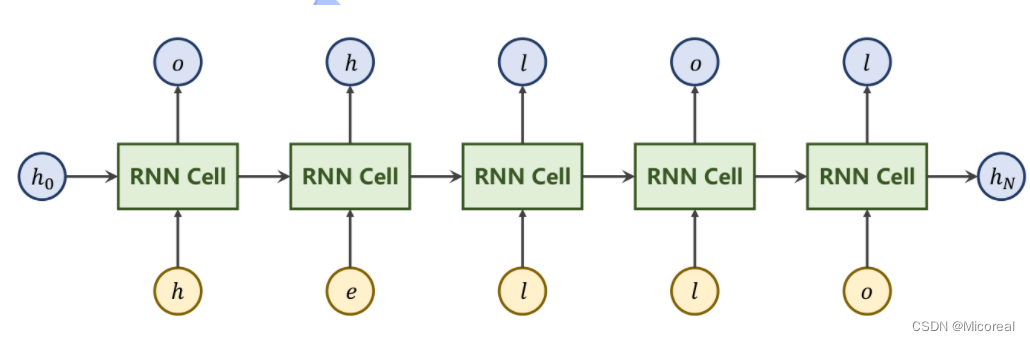
问题分析
原输入“hello”并不是一个向量,需要将其转变为一组数字向量。
对输入序列的每一个字符(单词)构造字典(词典),此时每一个字符都会有一个唯一的数字与其一一对应。即将字符向量转换为数字向量。之后利用独热编码(One-Hot)的思想,即可将每个数字转换为一个向量。
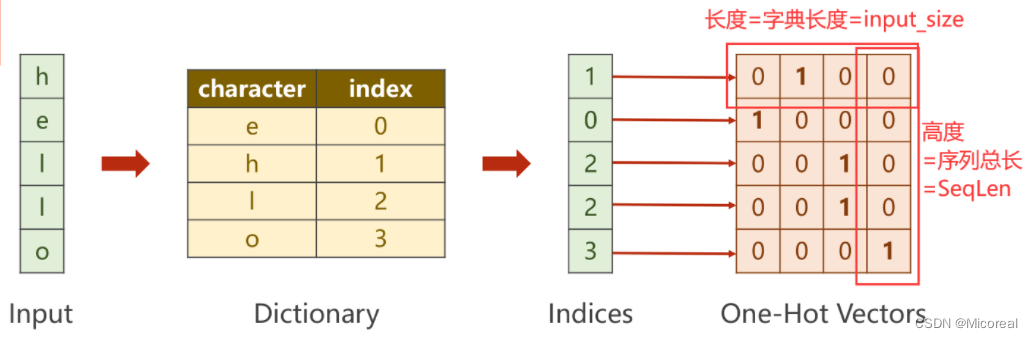
对输出序列按照上述要求构造字典。
多分类问题
对于序列中的每一个输入,都有一个数字输出与其对应,即本质上是在求当前输入所映射到输出字典中最大概率的值。即变为多分类问题。而此时的输出维度为3。
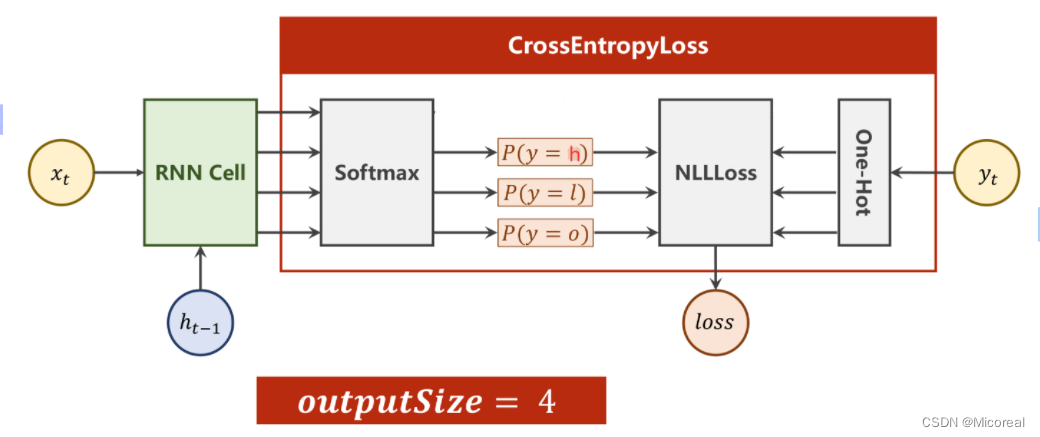
其中RNNCell的输出维度为4,经过Softmax求得映射之后的概率分别是多少,再利用输出对应的独热向量,计算NLLLoss。
代码
RNN Cell
import torch
input_size = 4
hidden_size = 3
batch_size = 1
#构建输入输出字典
idx2char_1 = ['e', 'h', 'l', 'o']
idx2char_2 = ['h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [2, 0, 1, 2, 1]
# y_data = [3, 1, 2, 2, 3]
one_hot_lookup = [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
#构造独热向量,此时向量维度为(SeqLen*InputSize)
x_one_hot = [one_hot_lookup[x] for x in x_data]
#view(-1……)保留原始SeqLen,并添加batch_size,input_size两个维度
inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)
#将labels转换为(SeqLen*1)的维度
labels = torch.LongTensor(y_data).view(-1, 1)
class Model(torch.nn.Module):
def __init__(self, input_size, hidden_size, batch_size):
super(Model, self).__init__()
self.batch_size = batch_size
self.input_size = input_size
self.hidden_size = hidden_size
self.rnncell = torch.nn.RNNCell(input_size = self.input_size,
hidden_size = self.hidden_size)
def forward(self, input, hidden):
# RNNCell input = (batchsize*inputsize)
# RNNCell hidden = (batchsize*hiddensize)
hidden = self.rnncell(input, hidden)
return hidden
#初始化零向量作为h0,只有此处用到batch_size
def init_hidden(self):
return torch.zeros(self.batch_size, self.hidden_size)
net = Model(input_size, hidden_size, batch_size)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.1)
for epoch in range(15):
#损失及梯度置0,创建前置条件h0
loss = 0
optimizer.zero_grad()
hidden = net.init_hidden()
print("Predicted string: ",end="")
#inputs=(seqLen*batchsize*input_size) labels = (seqLen*1)
#input是按序列取的inputs元素(batchsize*inputsize)
#label是按序列去的labels元素(1)
for input, label in zip(inputs, labels):
hidden = net(input, hidden)
#序列的每一项损失都需要累加
loss += criterion(hidden, label)
#多分类取最大
_, idx = hidden.max(dim=1)
print(idx2char_2[idx.item()], end='')
loss.backward()
optimizer.step()
print(", Epoch [%d/15] loss = %.4f" % (epoch+1, loss.item()))
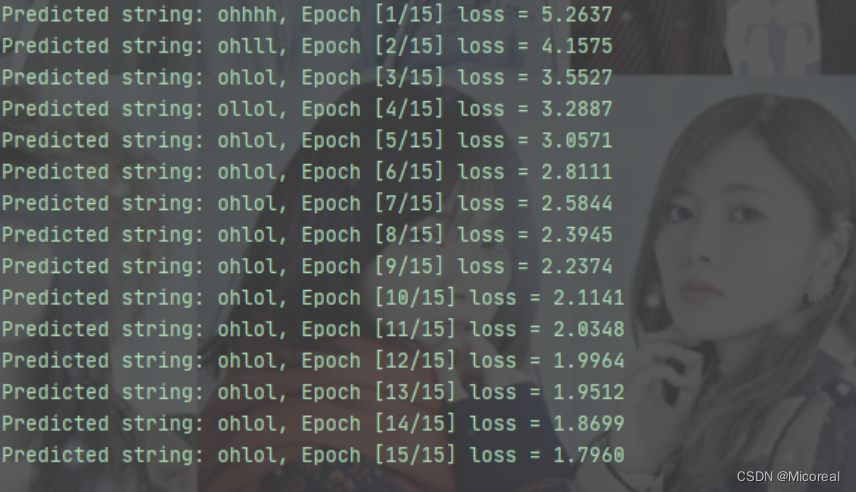
RNN
import torch
input_size = 4
hidden_size = 3
batch_size = 1
num_layers = 1
seq_len = 5
#构建输入输出字典
idx2char_1 = ['e', 'h', 'l', 'o']
idx2char_2 = ['h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [2, 0, 1, 2, 1]
# y_data = [3, 1, 2, 2, 3]
one_hot_lookup = [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]
inputs = torch.Tensor(x_one_hot).view(seq_len, batch_size, input_size)
#labels(seqLen*batchSize,1)为了之后进行矩阵运算,计算交叉熵
labels = torch.LongTensor(y_data)
class Model(torch.nn.Module):
def __init__(self, input_size, hidden_size, batch_size, num_layers=1):
super(Model, self).__init__()
self.batch_size = batch_size #构造H0
self.input_size = input_size
self.hidden_size = hidden_size
self.num_layers = num_layers
self.rnn = torch.nn.RNN(input_size = self.input_size,
hidden_size = self.hidden_size,
num_layers=num_layers)
def forward(self, input):
hidden = torch.zeros(self.num_layers,
self.batch_size,
self.hidden_size)
out, _ = self.rnn(input, hidden)
#reshape成(SeqLen*batchsize,hiddensize)便于在进行交叉熵计算时可以以矩阵进行。
return out.view(-1, self.hidden_size)
net = Model(input_size, hidden_size, batch_size, num_layers)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)
#RNN中的输入(SeqLen*batchsize*inputsize)
#RNN中的输出(SeqLen*batchsize*hiddensize)
#labels维度 hiddensize*1
for epoch in range(15):
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print('Predicted string: ',''.join([idx2char_2[x] for x in idx]), end = '')
print(", Epoch [%d/15] loss = %.3f" % (epoch+1, loss.item()))
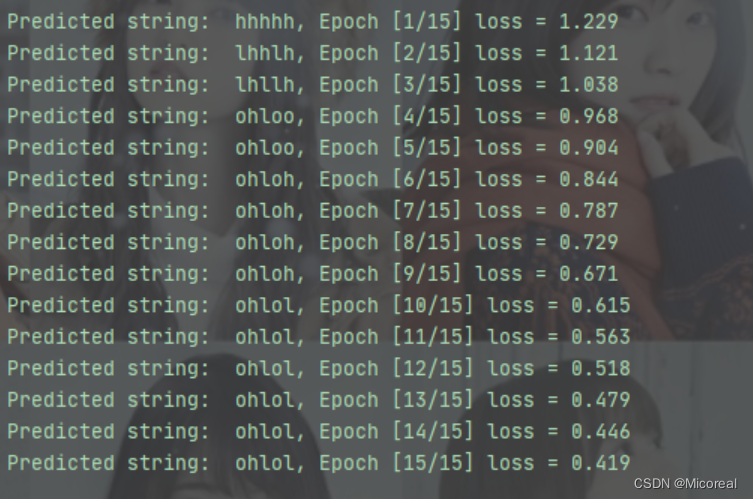
改进
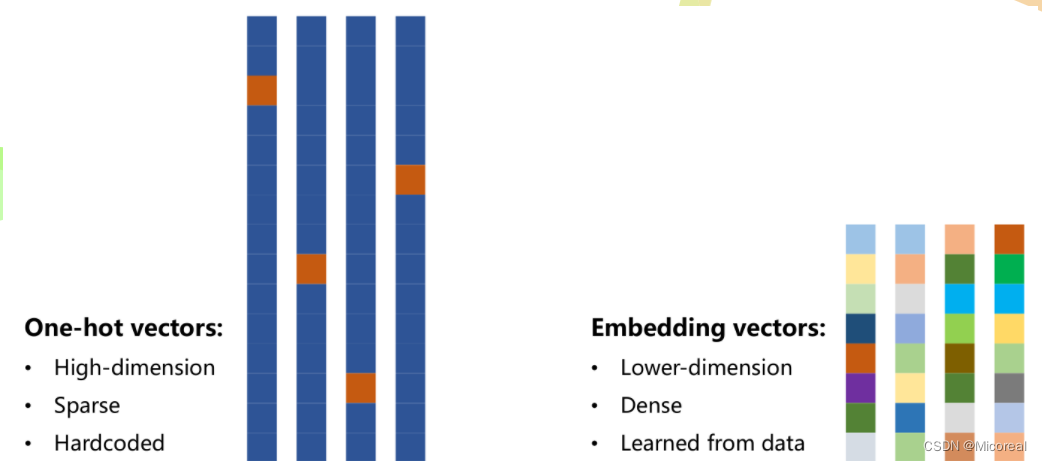
独热编码在实际问题中容易引起很多问题:
- 独热编码向量维度过高,每增加一个不同的数据,就要增加一维
- 独热编码向量稀疏,每个向量是一个为1其余为0
- 独热编码是硬编码,编码情况与数据特征无关
综上所述,需要一种低维度的、稠密的、可学习数据的编码方式
Embedding
目的是为了对数据进行降维
若从Input_Size转化为Embedding_Size,以下图为例,即需要把四维的向量转换为5维,则仅需要如下图所示的矩阵,将独热编码的向量与Embedding的矩阵相乘即可。
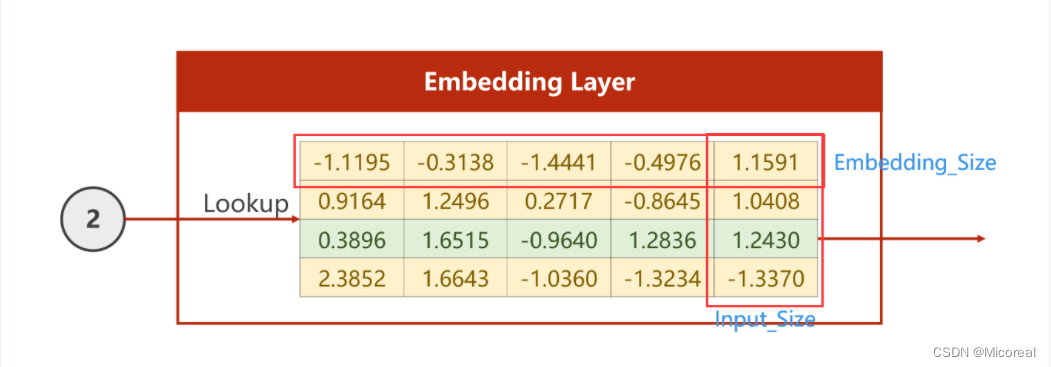
即将上图矩阵转置,再右乘向量即可

如此即可将原先四维的One-Hot编码变为五维的Embedding编码
网络结构
增加Embedding层实现降维,增加线性层使之在处理输入输出维度不同的情况下更加稳定。
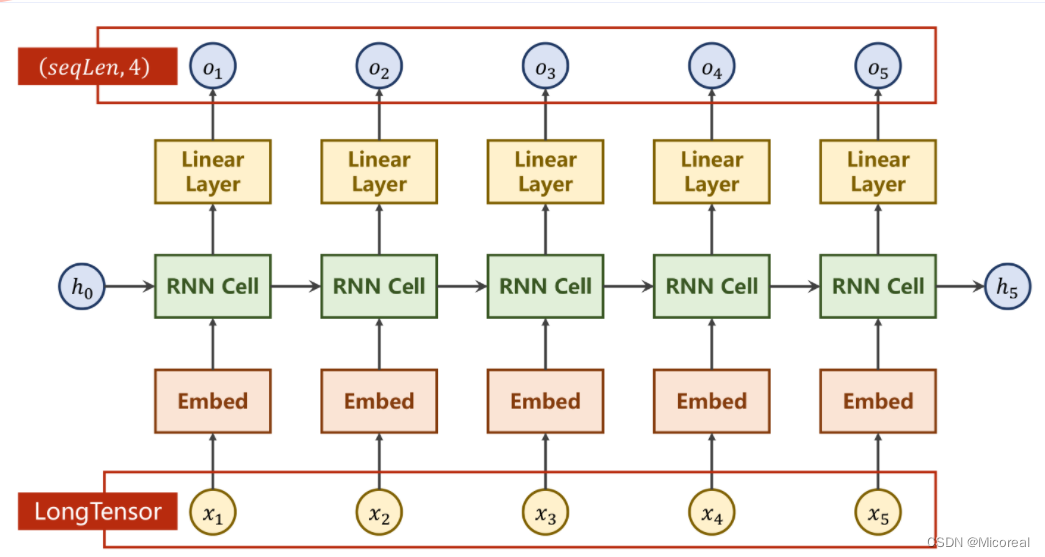
其中的Embedding层的输入必须是LongTensor类型。
Embedding说明
| 字段 | 类型 | 说明 |
|---|---|---|
| num_embedding | torch.nn.Embedding的参数 | 表示输入的独热编码的维数 |
| embedding_dim | torch.nn.Embedding的参数 | 表示需要转换成的维数 |
| Input | torch.nn.Embedding的输入量 | LongTensor类型 |
| Output | torch.nn.Embedding的输出量 | 为数据增加一个维度(embedding_dim) |
Linear说明
对于线性层,输入和输出的第一个维度(Batch)一直到倒数第二个维度都会保持不变。但会对最后一个维度(in_features)做出改变(out_features)

代码
import torch
input_size = 4
num_class = 4
hidden_size = 8
embedding_size =10
batch_size = 1
num_layers = 2
seq_len = 5
idx2char_1 = ['e', 'h', 'l', 'o']
idx2char_2 = ['h', 'l', 'o']
x_data = [[1, 0, 2, 2, 3]]
y_data = [3, 1, 2, 2, 3]
#inputs 作为交叉熵中的Inputs,维度为(batchsize,seqLen)
inputs = torch.LongTensor(x_data)
#labels 作为交叉熵中的Target,维度为(batchsize*seqLen)
labels = torch.LongTensor(y_data)
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self .emb = torch.nn.Embedding(input_size, embedding_size)
self.rnn = torch.nn.RNN(input_size = embedding_size,
hidden_size = hidden_size,
num_layers=num_layers,
batch_first = True)
self.fc = torch.nn.Linear(hidden_size, num_class)
def forward(self, x):
hidden = torch.zeros(num_layers, x.size(0), hidden_size)
x = self.emb(x)
x, _ = self.rnn(x, hidden)
x = self.fc(x)
return x.view(-1, num_class)
net = Model()
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)
for epoch in range(15):
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print('Predicted string: ',''.join([idx2char_1[x] for x in idx]), end = '')
print(", Epoch [%d/15] loss = %.3f" % (epoch+1, loss.item()))
输出结果: