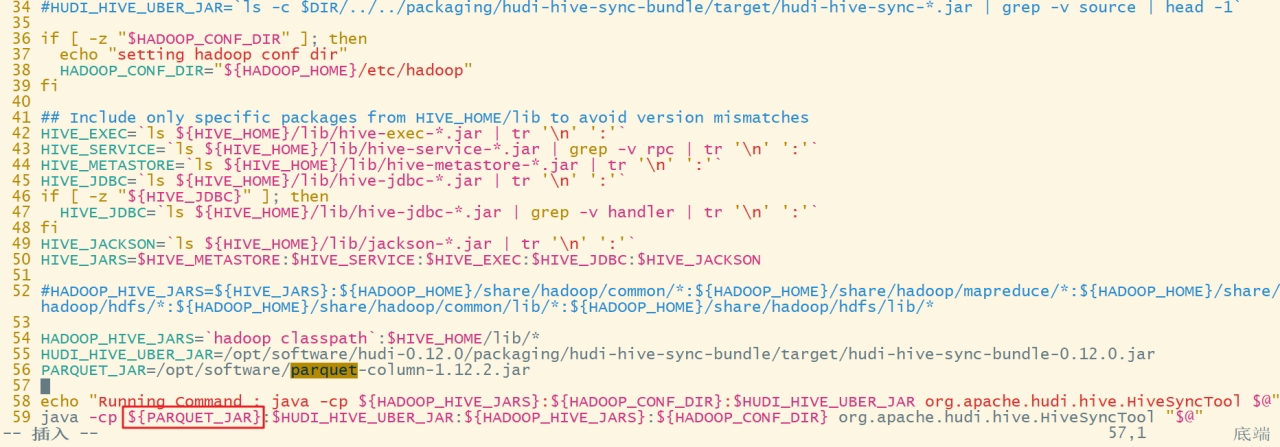
题目

做题过程
注:黄色高亮表示需要注意的地方,蓝色粗体表示代码思路
根据题意可以第一位数字为2,因此只需要考虑后面n-1位的排列,在这n-1位数字中,0和1的总数可能取2,3,……,n-2,当总数为 i 时,n-1个位置被0和1的组合所占用的情况有 C n − 1 i C_{n-1}^i Cn−1i种。我的第一个错误思路就直接将所有的 C n − 1 i C_{n-1}^i Cn−1i进行累加,这就忽略了组合内部的排序。在n-1位数字中,当0和1的总数为 i 时,对于每种对n-1个位置的占用情况,0出现的个数可能为1,2,……,i-1,因此共有 i-1 种排列。我的第二个错误思路将这考虑在内,但是却忽视了另一个组合2和3的组合中的内部排序。在n-1位数字中,当0和1的总数为 i 时,2和3的总数便为 n-1-i ,2出现的次数可能为0,1,2,……,n-2-i,共有 n-1-i 种情况。因此答案应该为 ∑ 2 n − 2 C n − 1 i × ( i − 1 ) × ( n − 1 − i ) \sum_2^{n-2}{C_{n-1}^i×(i-1)×(n-1-i)} ∑2n−2Cn−1i×(i−1)×(n−1−i)。这下思路就没有问题了。但是提交到系统后却只有30分,我便想到是不是int数据类型装不下大数,于是将一些可能涉及大数的变量类型更改为
long long,然而,分数只提高了10分。在网上参考了别人的代码后,发现别人的代码在很多地方进行了取模操作,而我只在最后一步取了模。我便去百度了一下模运算的性质,果然不出所料,问题就出现在这里。首先模运算的一些性质如下:
原来,如果我在中间操作过程中不去摸,会因为数太大而丢失数据,最后的答案自然不正确,而当在中间操作中进行取模后,根据运算规则可以保证最后取模的结果是正确的。
以后碰到操作大数的问题,一定要注意long long和取模这两个地方。
代码
#include <bits/stdc++.h>
using namespace std;
long long *Cs; //用动态数组表示杨辉三角
#define mod 1000000007
//杨辉三角位置到序号的映射
int GetOrder(int i, int j){//要定位的元素在杨辉三角的第i行第j列
return (i-1)*i/2 + j;
}
//构造杨辉三角
void makeC( ){
long long number = 999 * 500 + 1;
Cs = (long long *)malloc(sizeof(long long) * number);//元素从1位置拜访
Cs[1] = Cs[2] = Cs[3] = 1;
for(int i = 3; i < 1000; i++){
Cs[GetOrder(i,1)] = 1;
Cs[GetOrder(i,i)] = 1;
for(int j = 2; j < i; j++)
Cs[GetOrder(i,j)] = (Cs[GetOrder(i-1,j-1)] + Cs[GetOrder(i-1,j)])%mod;
}
}
//计算组合数
long long C(int a, int b){
return Cs[GetOrder(a+1,b+1)];
}
int main(){
int n;
long long ans = 0;
makeC();
scanf("%d",&n);
for(int i = 2; i < n-1; i++){
ans += ((C(n-1, i) * (i - 1)%mod) * (n - i - 1))%mod;
}
ans%=mod;
printf("%d",ans);
return 0;
}
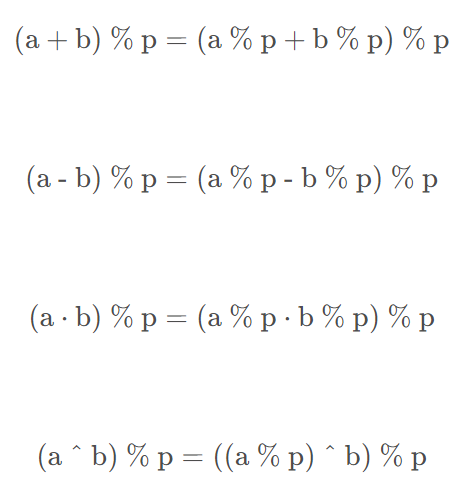






![[chatGPT] 如何通过JNI在Android上显示实时视频流](https://img-blog.csdnimg.cn/de6c4256ef734f3d90544d68d613ebec.png)