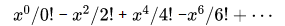前言

shapely是基于笛卡尔坐标的几何对象操作和分析Python库。底层基于GEOS和JTS库。shapely无法读取和写数据文件，但可以基于应用广泛的一些格式和协议进行序列化(serialize)和去序列化(deserialize)操作。而且shapely不关注数据格式和坐标系统，但shapely的整合性很强，可以和GIS之类的工具协同工作。这种黏性类似python。

1、安装

（1）基于构建的发行版

windows

conda install shapely

基于 wheels 安装 (http://www.lfd.uci.edu/~gohlke/pythonlibs/#shapely)

Mac OS和Linux

pip install shapely，如果需要针对向量化加速版本可通过pip install shapely[vectorized]安装

通过系统包管理器，比如 apt，yum 和 Homebrew等。

也可以通过Canopy和Anaconda等Python发行版工具安装，比如Anaconda，conda install shapely

（2）基于源码

当需要兼容基于GEOS的更多模块，或者想要使用不同的GEOS版本，可以基于源码进行安装：

pip install shapely --no-binary shapely

如果使用自定义GEOS版本进行安装时，可能需要指定geos-config程序的路径，

GEOS_CONFIG=/path/to/geos-config pip install shapely

2、基本操作

（1）创建点

from shapely.geometry import Point
  
point = Point(0, 0) # Point((0, 0))
  
point.area    # 获取点的面积
point.length  # 获取点的长度
point.bounds  # 获取点的边界

（2）创建圆

In [20]: circle = Point(0, 0).buffer(10) # 创建以(0, 0)为圆心，10为半径的圆
  
In [25]: circle.area  # 获取创建的圆的面积
Out[25]: 313.6548490545939

从上述结果可以看出，所创建的圆的面积小于 $\text{[math]}$ ，这是因为buffer方法默认参数resolution为16，resolution 的值越大圆越完整。

In [30]: circle = Point(0, 0).buffer(10, resolution=1000)
  
In [31]: circle.area
Out[31]: 314.15913616617644
      
In [32]: circle = Point(0, 0).buffer(10, resolution=1000000)
  
In [33]: circle.area
Out[33]: 314.1592653588436

（3）创建多边形

from shapely.geometry import Polygon
  
polygon = Polygon([(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3), (0, 3)])

Polygon 函数仅能基于有序的点创建多边形，且点的集合必须要是闭合的。使用MultiPoint 函数创建，并使用 convex_hull 方法创建多边形。

from shapely.geometry import MultiPoint
  
coords = [(0, 1), (1, 2), (1, 4), (2, 0), (3, 2)]  # coords不一定要是闭合点集合
poly = MultiPoint(coords).convex_hull

3、集合操作

（1）判断点是否在多边形

In [50]: p1 = Point(24.952242, 60.1696017)
In [51]: p2 = Point(24.976567, 60.1612500)
In [52]: coords = [(24.950899, 60.169158), (24.953492, 60.169158), (24.953510, 60.170104), (24.950958, 60.169990)]
In [53]: poly = Polygon(coords)

In [54]: poly.contains(p1)
Out[54]: True

In [55]: p1.within(poly)
Out[55]: True

In [56]: poly.contains(p2)
Out[56]: False

（2）判断多边形的集合操作

In [57]: poly2 = Polygon([(23.2154, 59.1156), (24.83151, 59.41516), (25.11667, 60.311561), (24.16178, 60.13315)] )
    
In [58]: poly2.intersects(poly)
Out[58]: True
    
In [59]: poly2.contains(poly)
Out[59]: True
    
In [60]: poly.contains(poly2)
Out[60]: False