数楼梯(加强版)

题目背景:

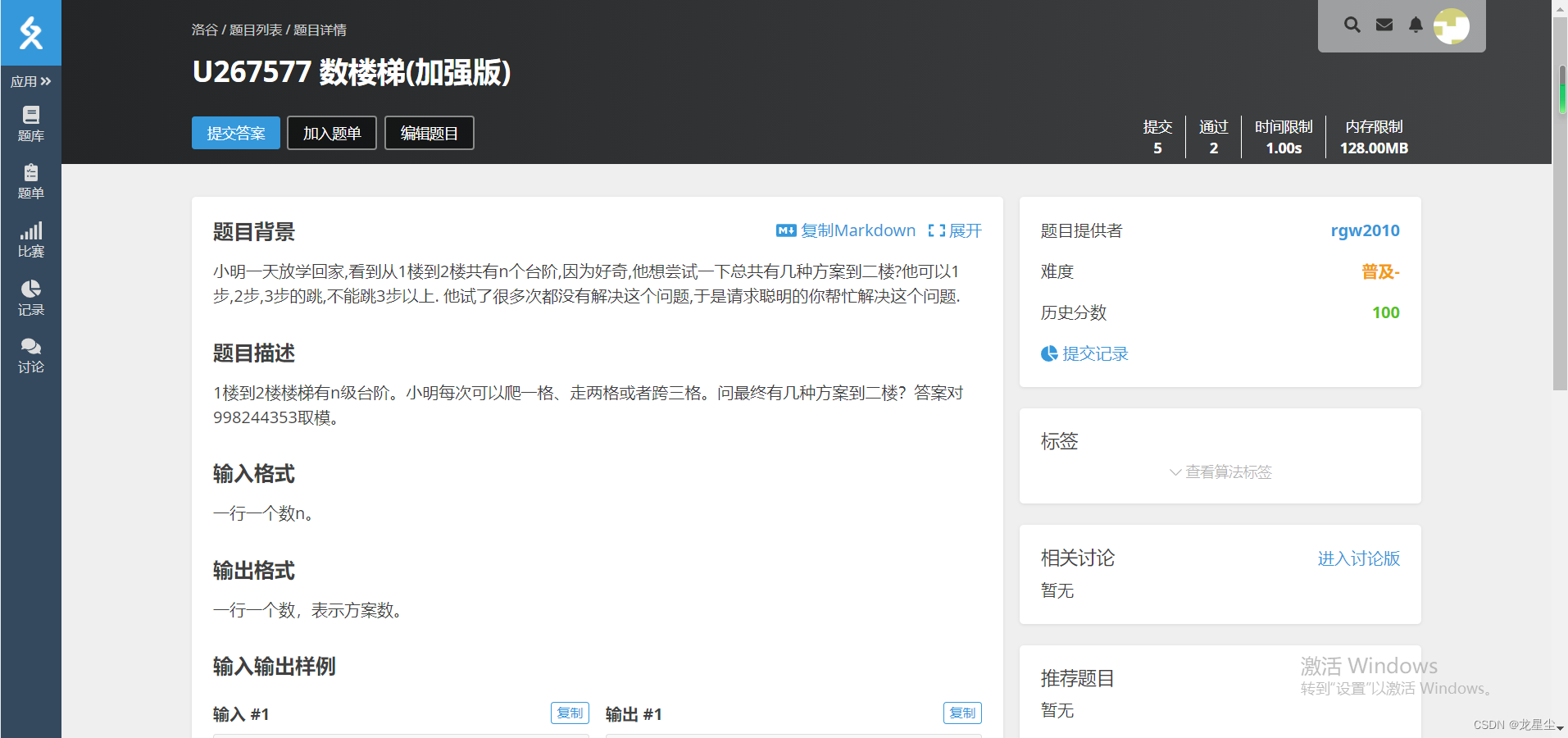
小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上.
他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题.

题目描述:

1楼到2楼楼梯有n级台阶。小明每次可以爬一格、走两格或者跨三格。问最终有几种方案到二楼？答案对998244353取模。

输入格式:

一行一个数n。

输出格式:

一行一个数，表示方案数。

输入输出样例

输入 #1:

输出 #1:

输入 #2:

输出 #2:

提示说明:

n≤1000
时间：1000ms
空间：256M
(上楼梯时不能往回走)
如果觉得这道题太难可以前往P1255先做数楼梯简单版：
https://www.luogu.com.cn/problem/P1255

思路:

1.暴力法

很容易看出来，这是一道递归题，我们可以用暴力递归来解决。

#include<iostream> 
using namespace std; 
static const int mod=998244353;
long long sum=0;
int n;
long long fun(int x){
	if(x==n)
	  return 1;
	if(x>n)
	  return 0;
	long long s1=0,s2=0,s3=0;
	s1+=fun(x+1)%mod;
	s2+=fun(x+2)%mod;
	s3+=fun(x+3)%mod;
	return (s1+s2+s3)%mod;
}
int main(){
	cin>>n;
	cout<<fun(0)<<endl;		
    return 0;
}

但是这个份代码会超时，非常慢，所以要进行优化！

2.递推法

我们用 f(x) 表示爬到第 x 级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以我们可以列出如下式子：
f(x)=f(x−1)+f(x−2)
它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解，因为每次只能爬 1 级或 2 级，所以 f(x) 只能从 f(x−1)和 f(x−2) 转移过来，而这里要统计方案总数，我们就需要对这两项的贡献求和。

以上是动态规划的转移方程，下面我们来讨论边界条件。我们是从第 0 级开始爬的，所以从第 0 级爬到第 0 级我们可以看作只有一种方案，即 f(0)=1；从第 0 级到第 1 级也只有一种方案，即爬一级，f(1)=1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下，根据转移方程得到 f(2)=2，f(3)=3，f(4)=5，……，我们把这些情况都枚举出来，发现计算的结果是正确的。

我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n)的实现，但是由于这里的 f(x) 只和 f(x−1)) 与 f(x−2)有关，所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。下面的代码中给出的就是这种实现。

#include<iostream> 
using namespace std; 
static const int mod=998244353;
void fun(int n){
	long long max[1001];
	int i=0;
	max[0]=1;
	max[1]=2;
	max[2]=4;
	for(int j=3;j<n;j++)
	  max[j]=(max[j-1]+max[j-2]+max[j-3])%mod;
	cout<<max[n-1]<<endl;
}
int main(){
	int n;
	cin>>n;
	fun(n);		
    return 0;
}