电子技术——DC偏移

因为差分放大器是直接耦合的并且对于DC有着有限的增益，因此本节我们讨论差分放大器在DC相关方面的问题。

MOS差分放大器的输入偏移电压

考虑下面的电路，我们将MOS差分放大器的输入端都置地：

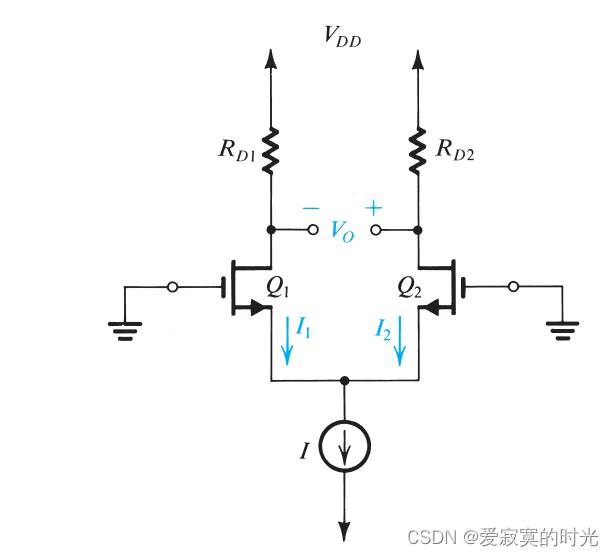
此时假如电路完全对称，那么 $V_O$ 本应该等于零，但是由于实际电路中的非理想因素存在，若电路不完全对称，那么即使输入两端均置地 $V_O$ 也不为零。我们称此时的 $V_O$ 为 输出DC偏移电压 。进一步我们将其除以差分增益 $A_d$ 我们称其为 输入偏移电压 ：

$$V_{OS}=V_O/A_d$$

若我们在输入端应用差分电压 $-V_{OS}$ 那么 $V_O$ 就会减小到零，如图：

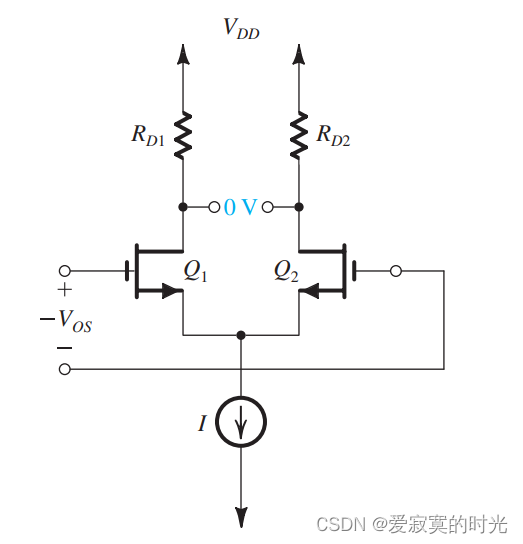
这对于偏移电压给了我们一个直观的感受。应该注意，因为偏移电压是电路不匹配造成的，因此极性无法提前预知。

总共有三个因数造成了DC偏移：负载电阻不匹配， $W/L$ 不匹配，以及 $V_t$ 不匹配。

首先我们考虑 $Q_1$ 和 $Q_2$ 完全匹配，但是负载电阻不匹配的情况，也就是：

$$R_{D1}=R_D+\frac{\Delta R_D}{2}$$

$$R_{D2}=R_D-\frac{\Delta R_D}{2}$$

因此输出电压为：

$$V_{D1}=V_{DD}-\frac{I}{2}(R_D+\frac{\Delta R_D}{2})$$

$$V_{D2}=V_{DD}-\frac{I}{2}(R_D-\frac{\Delta R_D}{2})$$

因此差分电压为：

$$V_O=V_{D2}-V_{D1}=\frac{I}{2}\Delta R_D$$

通过除以 $A_d=g_m{R}_D$ 得到：

$$V_{OS}=\frac{V_{OV}}{2}\frac{\Delta R_D}{R_D}$$

接下来，考虑 $W/L$ 不匹配的情况：

$$(\frac{W}{L}{)}_1=\frac{W}{L}+\frac{1}{2}\Delta (\frac{W}{L})$$

$$(\frac{W}{L}{)}_2=\frac{W}{L}-\frac{1}{2}\Delta (\frac{W}{L})$$

因为 $V_{GS1}=V_{GS2}$ 所以两个漏极电流之比等于 $W/L$ 之比，并且总和仍为 $I$ 解得：

$$I_1=\frac{I}{2}[1+\frac{\Delta (\frac{W}{L})}{2(\frac{W}{L})}]$$

$$I_2=\frac{I}{2}[1-\frac{\Delta (\frac{W}{L})}{2(\frac{W}{L})}]$$

则输出电压为：

$$V_O=\frac{I}{2}\frac{\Delta (\frac{W}{L})}{(\frac{W}{L})}{R}_D$$

除以 $A_d$ 得到：

$$V_{OS}=(\frac{V_{OV}}{2})(\frac{\Delta (W/L)}{(W/L)})$$

最后我们考虑 $V_t$ 不匹配的情况，即：

$$V_{t1}=V_t+\frac{\Delta V_t}{2}$$

$$V_{t2}=V_t-\frac{\Delta V_t}{2}$$

这给出电流：

$$I_1=\frac{1}{2}{k}_n^{\prime }\frac{W}{L}(V_{GS}-V_t-\frac{\Delta V_t}{2}{)}^2=\frac{1}{2}{k}_n^{\prime }\frac{W}{L}(V_{GS}-V_t{)}^2(1-\frac{\Delta V_t}{2(V_{GS}-V_t)}{)}^2$$

假设 $\Delta V_t\ll 2(V_{GS}-V_t)$ 则：

$$I_1\simeq \frac{1}{2}{k}_n^{\prime }\frac{W}{L}(V_{GS}-V_t{)}^2(1-\frac{\Delta V_t}{V_{GS}-V_t})$$

$$I_2\simeq \frac{1}{2}{k}_n^{\prime }\frac{W}{L}(V_{GS}-V_t{)}^2(1+\frac{\Delta V_t}{V_{GS}-V_t})$$

因为 $V_t$ 的变化不会引起 $V_{GS}$ 的变化，所以：

$$\frac{1}{2}{k}_n^{\prime }\frac{W}{L}(V_{GS}-V_t{)}^2=\frac{I}{2}$$

则电流差为：

$$V_O=\frac{I\Delta V_t}{V_{OV}}{R}_D$$

则除以 $g_m{R}_D$ 为：

$$V_{OS}=\Delta V_t$$

最终，我们发现三个因素是不相关因素，因此存在一个简单的模型来综合这三个因素的影响：

$$V_{OS}=\sqrt{(\frac{V_{OV}}{2}\frac{\Delta R_D}{R_D}{)}^2+[(\frac{V_{OV}}{2})(\frac{\Delta (W/L)}{(W/L)}){]}^2+(\Delta V_t{)}^2}$$

BJT差分放大器的输入偏移电压

同样的BJT差分放大器也存在输入偏移电压，这是由：负载电阻不匹配，截面积不匹配， $\beta$ 不匹配和其他BJT不匹配因素造成的。

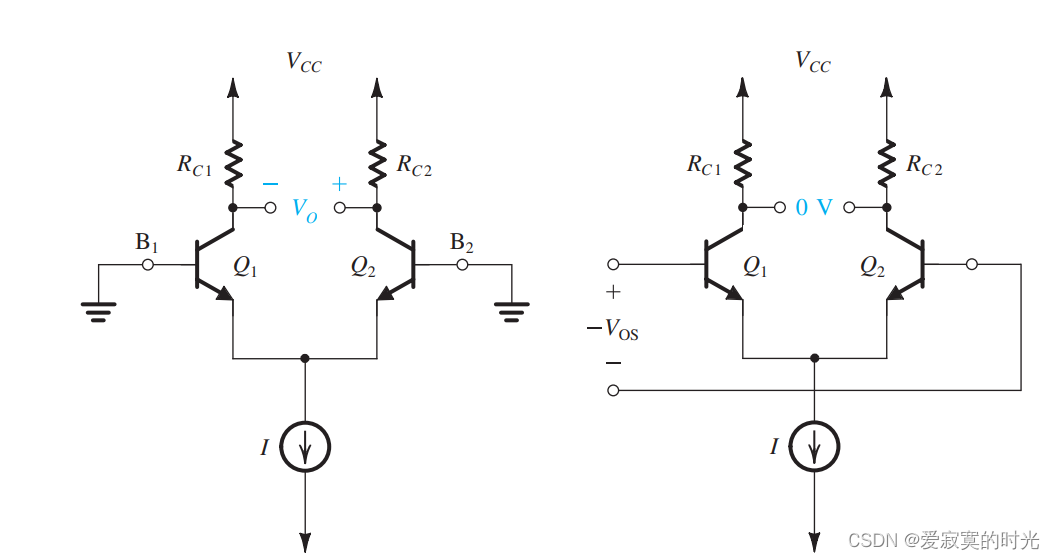
首先考虑负载电阻不匹配：

$$R_{C1}=R_C+\frac{\Delta R_C}{2}$$

$$R_{C2}=R_C-\frac{\Delta R_C}{2}$$

假设BJT完全匹配，则输出电压为：

$$V_{C1}=V_{CC}-(\frac{\alpha I}{2})(R_C+\frac{\Delta R_C}{2})$$

$$V_{C2}=V_{CC}-(\frac{\alpha I}{2})(R_C-\frac{\Delta R_C}{2})$$

则输出电压为：

$$V_O=V_{C2}-V_{C1}=\alpha (\frac{I}{2})(\Delta R_C)$$

增益为：

$$A_d=g_m{R}_C=\frac{\alpha I/2}{V_T}{R}_C$$

则输入电压偏移为：

$$|V_{OS}|=V_T\frac{\Delta R_C}{R_C}$$

需要注意的一点是 $V_T$ 要小于 $V_{OV}/2$ ，说明在同等的情况下，BJT的DC偏移要比MOS的DC偏移小。

接下来我们考虑 $Q_1$ 和 $Q_2$ 不匹配。特别的，我们假设BJT的截面积不相同，这给出缩放电流 $I_S$ 不相同：

$$I_{S1}=I_S+\frac{\Delta I_S}{2}$$

$$I_{S2}=I_S-\frac{\Delta I_S}{2}$$

注意到 $V_{BE1}=V_{BE2}$ 所以发射极电流只和 $I_S$ 成正比，并且保存和为 $I$ 解得：

$$I_{E1}=\frac{I}{2}(1+\frac{\Delta I_S}{2I_S})$$

$$I_{E2}=\frac{I}{2}(1-\frac{\Delta I_S}{2I_S})$$

则输出电压为：

$$V_O=\alpha (\frac{I}{2})(\frac{\Delta I_S}{I_S})R_C$$

对应的输入偏移为：

$$|V_{OS}|=V_T(\frac{\Delta I_S}{I_S})$$

再一次我们注意到，BJT不想MOS正比于 $V_{OV}$ 而是正比于 $V_T$ ，说明在同等的情况下，BJT的DC偏移要比MOS的DC偏移小。

因为两个因素不相同，所以存在一个估算模型：

$$V_{OS}=\sqrt{(V_T(\frac{\Delta I_S}{I_S}){)}^2+(V_T\frac{\Delta R_C}{R_C}{)}^2}$$

我们只推算这两种情况，实际上BJT还受 $\beta$ 和 $r_o$ 的影响。无论是MOS还是BJT都存在DC偏移电压，因此在电路设计师通常设计 偏移归零 电路，使得当输入相等电压的时候，输出总为零。

BJT差分放大器的输入偏置和偏移电流

由于BJT存在有限的基极电流，当BJT完美匹配的时候，此时基极电流相等：

$$I_{B1}=I_{B2}=\frac{I/2}{\beta +1}$$

这称为BJT差分放大器的 输入偏置电流 。

当BJT不完美匹配的时候，此时基极电流不相等，我们称此时基极电流的差值为 输入偏移电流 $I_{OS}$ ：

$$I_{OS}=|I_{B1}-I_{B2}|$$

特别的，我们假设 $\beta$ 不同：

$${\beta }_1=\beta +\frac{\Delta \beta }{2}$$

$${\beta }_2=\beta -\frac{\Delta \beta }{2}$$

我们假设 $\Delta \beta$ 足够小，则两路电流仍可看成相等均为 $I/2$ ，然后：

$$I_{B1}=\frac{I}{2}\frac{1}{\beta +1+\Delta \beta /2}\simeq \frac{I}{2}\frac{1}{\beta +1}(1-\frac{\Delta \beta }{2\beta })$$

$$I_{B2}=\frac{I}{2}\frac{1}{\beta +1-\Delta \beta /2}\simeq \frac{I}{2}\frac{1}{\beta +1}(1+\frac{\Delta \beta }{2\beta })$$

$$I_{OS}=\frac{I}{2(\beta +1)}(\frac{\Delta \beta }{\beta })$$

一般的，我们定义偏移电流为：

$$I_B\equiv \frac{I_{B1}+I_{B2}}{2}=\frac{I}{2(\beta +1)}$$

因此：

$$I_{OS}=I_B(\frac{\Delta \beta }{\beta })$$

最后一点，MOS因为其没有栅极电流，因此MOS不受输入偏置和偏移电流的影响。