哈希表(Hash table)
也叫散列表,是根据键(Key)而直接访问在内存存储位置的数据结构。也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
一、什么是哈希表
在讨论哈希表之前,我们先大概了解下其他数据结构
数组:
采用一段连续的存储单元来存储数据。
对于指定下标的查找,时间复杂度为O(1);
通过给定值进行查找,需要遍历数组,逐一比对给定关键字和数组元素,时间复杂度为O(n),
对于有序数组,则可采用二分查找,插值查找,斐波那契查找等方式,可将查找复杂度提高为O(logn);对于一般的插入删除操作,涉及到数组元素的移动,其平均复杂度也为O(n)
线性链表:
对于链表的新增,删除等操作(在找到指定操作位置后),仅需处理结点间的引用即可,时间复杂度为O(1),而查找操作需要遍历链表逐一进行比对,复杂度为O(n)
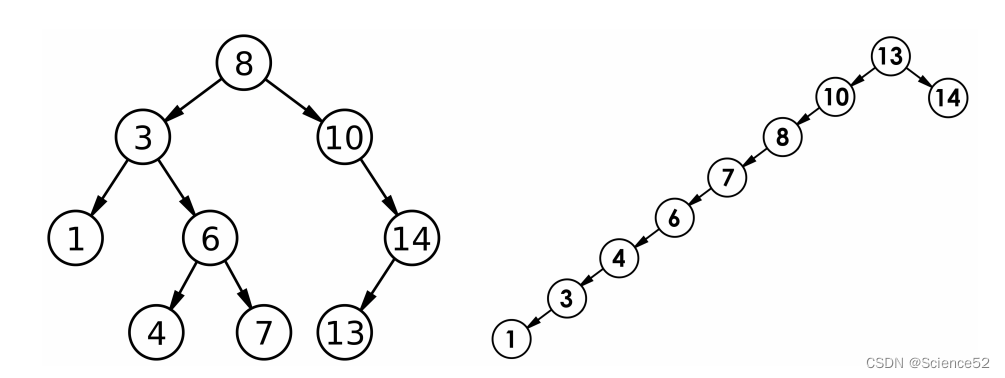
二叉树:
对一棵相对平衡的有序二叉树,对其进行插入,查找,删除等操作,平均复杂度均为O(logn)。
哈希表:
相比上述几种数据结构,在哈希表中进行添加,删除,查找等操作,性能十分之高,不考虑哈希冲突的情况下(后面会探讨下哈希冲突的情况),仅需一次定位即可完成,时间复杂度为O(1),接下来我们就来看看哈希表是如何实现达到惊艳的常数阶O(1)的。
我们知道,数据结构的物理存储结构只有两种:顺序存储结构和链式存储结构(像栈,队列,树,图等是从逻辑结构去抽象的,映射到内存中,也这两种物理组织形式),而在上面我们提到过,在数组中根据下标查找某个元素,一次定位就可以达到,哈希表利用了这种特性,哈希表的主干就是数组。
比如我们要新增或查找某个元素,我们通过把当前元素的关键字 通过某个函数映射到数组中的某个位置,通过数组下标一次定位就可完成操作。
这个函数可以简单描述为:存储位置 = f(关键字) ,这个函数f一般称为哈希函数,这个函数的设计好坏会直接影响到哈希表的优劣。
插入过程如下图所示
哈希冲突
如果两个不同的元素,通过哈希函数得出的实际存储地址相同怎么办?
也就是说,当我们对某个元素进行哈希运算,得到一个存储地址,然后要进行插入的时候,发现已经被其他元素占用了,其实这就是所谓的哈希冲突,也叫哈希碰撞。
前面我们提到过,哈希函数的设计至关重要,好的哈希函数会尽可能地保证 计算简单和散列地址分布均匀,但是,我们需要清楚的是,数组是一块连续的固定长度的内存空间,再好的哈希函数也不能保证得到的存储地址绝对不发生冲突。
那么哈希冲突如何解决呢?
哈希冲突的解决方案有多种:
开放定址法(发生冲突,继续寻找下一块未被占用的存储地址),再散列函数法,链地址法,而HashMap即是采用了链地址法,也就是数组+链表的方式。
HashMap
基于哈希表的 Map 接口的实现。此实现提供所有可选的映射操作,并允许使用 null 值和 null 键。(除了非同步和允许使用 null 之外,HashMap 与 Hashtable 大致相同)此类不保证映射的顺序,特别是它不保证该顺序恒久不变。
实现假定哈希函数将元素适当地分布在各桶之间,可为基本操作(get 和 put)提供稳定的性能。迭代 collection 视图所需的时间与 HashMap 实例的“容量”(桶的数量)及其大小(键-值映射关系数)成比例。所以,如果迭代性能很重要,则不要将初始容量设置得太高(或将加载因子设置得太低)。
二、HashMap的实现原理
1、HashMap的内部结构

HashMap是数组加链表组成的复合结构,HashMap的主干是数组,其中数组被分为一个个桶(bucket),每个桶存储有一个或多个键值对,每个键值对也称为 Entry ,通过哈希值决定了Entry对象在这个数组的下标;哈希值相同的Entry对象(键值对),则以链表形式存储。
注意:HashMap中数组长度的原始大小为16,且数组的初始值都为null。
2.工作过程
(1)存(Put)
传入第一个键值对Entry1时,会通过哈希函数hash()计算key的值,那么就将键值对 Entry1 放入到对应下标中。
插入的Entry会越来越多,这个时候又该如何存储呢?
这个时候就需要用到链表了。
如果 Entry2 通过哈希函数计算得到的下标,而此下标处有一个 Entry1,这时就出现了“hash冲突”。该如何插入呢?
HashMap数组的每一个元素不止是一个Entry对象,每一个Entry对象通过Next指针指向它的下一个Entry节点。当新来的Entry映射到冲突的数组位置时,只需要插入到对应的链表即可,而插入是根据“头插法”进行插入。
(2)修改Entry中value的过程:
修改Entry中value的过程和存是差不多的,多了一个比较
先查询链表,根据equals方法,查询当前的key是否存在,如果存在,则用新的Entry覆盖旧的Entry。如果不存在则再次使用“头插法”将当前Entry插入到链表中。
(3)读(Get)
首先根据哈希函数计算出key的hash值,这就是HashMap对应的下标,根据下标的链表来查询key。
使用equals方法比对Entry的key,如果返回结果为false,则继续查询,如果返回结果为ture,表示已经匹配到了正确的key,再获取对应的value
三丶JDK1.7月JDK1.8中HashMap的区别
在jdk1.7中HashMap主要结构为:数组+链表。
在jdk1.8中HashMap主要结构为:数组+链表+红黑树。
为什么要加入红黑树呢?学过的人都应该知道,红黑树查询是非常快的。
设想一个情况,当我们插入的Entry非常多时,我们的链表会长的可怕,这个时候去遍历链表寻找对应的key,所花费的时间可想而知的恐怖。
加入红黑树可以优化查询的时间,使查询效率快上不少。
那么在jdk1.8的HashMap中,当链表的长度超过8时,链表会自动转化为红黑树,优化查询速度。
同时还有一个区别:发生“hash冲突”时,我们上面的做法是“头插法”,这是jdk1.7的做法,而在jdk1.8中,使用的是“尾插法”。