原始值函数

原始GAN的值函数是
$$mi{n}_{G}ma{x}_{D}V(D,G)=E_{x\sim p_{data}(x)}[logD(x)]+E_{z\sim p_z(z)}[log(1-D(G(z)))]$$
其中$E_{x\sim p_{data}(x)}$表示从真实样本采样，$E_{z\sim p_z(z)}$表示从噪声样本中采样
进一步将V(D,G)写成积分格式就是
$$\begin{gathered} V(G,D)={\int }_x{p}_{data}(x)log(D(x))dx+{\int }_z{p}_z(z)log(1-D(g(z)))dz \\ V(G,D)={\int }_x{p}_{data}(x)log(D(x))dx+p_g(x)log(1-D(x))dx \end{gathered}$$
For any (a, b) ∈ R2, the function y → a log(y) + b log(1 − y) achieves its maximum at a/(a+b).

优化饱和

**在实际训练中，早期G很差，G生成的样本很容易被D识别，使得D回传给G的梯度极小，达不到训练目标，这种现象叫做优化饱和。**进一步解释一下优化饱和的原因，将D的sigmoid输出层的前一层记为o，那么D(x)=Sigmoid(o(x))，那么
$$\nabla D(x)=\nabla Sigmoid(o(x))=D(x)(1-D(x))\nabla o(x)$$
所以训练G时候的梯度里包含的D(G(x))就趋近于0
解决方案是把$log(1-D(G(z)))$改成$log(D(G(z)))$,$mi{n}_G$变成了$ma{x}_G$

WGAN-GP

普通的GAN可以看做是优化JS距离，但是只用JS距离会进入坍缩模式（拿图片举例，反复生成一些相近或相同的图片，多样性太差。生成器似乎将图片记下，没有泛化，更没有造新图的能力，好比一个笨小孩被填鸭灌输了知识，只会死记硬背，没有真正理解，不会活学活用，更无创新能力）。猜测问题根源和JS距离维度低有关系，因此引入了Wasserstein距离（也叫推土机距离，Earth Mover distance）。

为什么Wasserstein距离能克服JS距离解决不了的问题？理论上的解释很复杂，需要证明当生成器分布随参数θ变化而连续变化时，生成器分布与真实分布的Wasserstein距离也随θ变化而连续变化，并且几乎处处可导，而JS距离不保证随θ变化而连续变化。
推土机距离实际中非常难求，但是有个Wasserstein距离对偶式比较好求解：
$$mi{n}_{G}ma{x}_{||f|{|}_L<=1}E(f(x))-E(f(\tilde{x}))$$
其中$||f|{|}_L<=1$是1-Lipschitz函数（对于函数f(x),若其任意定义域中的x1,x2，都存在L>0，使得|f(x1)-f(x2)|≤L|x1-x2|。 大白话就是：存在一个实数L，使得对于函数f（x）上的每对点，连接它们的线的斜率的绝对值不大于这个实数L。）。其实x是real，$\tilde{x}$是生成，上面这个其实就是把原始GAN值函数的Log也去掉。

实际中发现The interaction between the weight constraint and the loss function makes training of WGAN difficult and leads to exploding or vanishing gradients.解决方案直接把1-Lipschitz的约束变成了Gradient Penalty（The idea of Gradient Penalty is to enforce a constraint such that the gradients of the critic’s output w.r.t the inputs to have unit norm）。因此最终的目标函数变成了

判别器也换了一个名字叫做Critic评分器

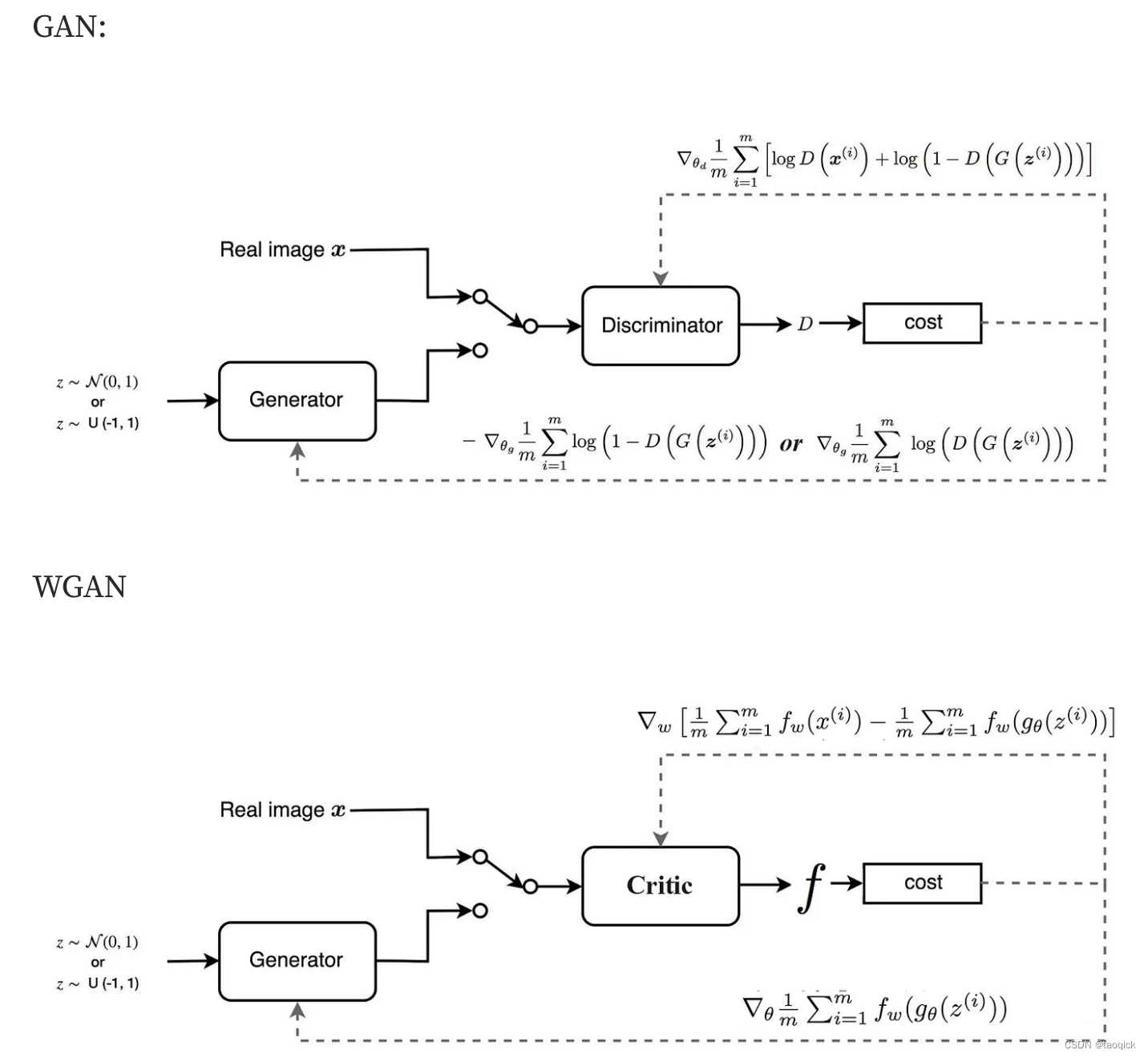
Spectral Normalization

为了让判别器函数满足 1-Lipschitz continuity，W-GAN 和之后的 W-GAN GP 分别采用了 weight-clipping 和 gradient penalty 来约束判别器参数。这里的谱归一化，则是另一种让函数满足 1-Lipschitz continuity 的方式。谱归一化会对每一层的权重做奇异值分解，并对奇异值做归一化以将其限制在1以内

IPM(Integral Probability Metrics)-GAN

IPM-GAN基于积分概率度量两个分布的距离，WGAN是一种典型的IPM-GAN，另外一种典型的IPM-GAN叫做McGAN（Mean and Covariance Feature Matching GAN）。它从最小化IPM的角度将分布之间距离的度量定义为有限维度特征空间的分布匹配。

首先，分类超平面搜索；然后，判别器向远离超平面的方向更新；最后，生成器向超平面的方向更新。实际上，这种几何解释同样可以应用在其他GAN上，包括f-GAN、WGAN等。各种GAN之间的主要区别就在于分类超平面的构建方法以及特征向量的几何尺度缩放因子的选择

DC-GAN

DCGAN全称Deep Convolutional GAN，发表于ICLR2016。DCGAN的主要贡献反卷积操作又称为“分数步长卷积”（fractional-strided convolution）或“转置卷积”（transposed convolution），可以视为一种与正常卷积“相反”的操作，这里不是指反卷积是卷积的逆变换，而是使用一种类似卷积的方法实现了上采样

ALI(Adversarially learned inference)

Adversarially Learned Inference（简称ALI）与Adversarial feature learning（简称BiGAN）类似，GAN中的生成器实现了从Latent向量空间z到图像空间x的转换，ALI和BiGAN模型则添加了图像空间x到Latent向量空间z的转换。判别器不仅需要学习区分生成的样本和真实的样本，还需要区分两个不同的数据和潜在变量联合分布。

IRGAN

给定q，生成模型会在整个文档集中按照概率分布$p_{\theta }(d|q)$挑选出文档dθ，它的目标是逼近真实数据的概率分布ptrue(d|q)，进而迷惑判别器；同时，判别模型试图将生成器伪造的(q,dθ)从真实的(q,dtrue)中区分出来。原本的判别模型是用来鉴别与Query相关或不相关的文档，而在GAN框架下判别模型的目标发生了微妙变化，区分的是来自真实数据的相关文档和模拟产生的潜在相关文档。当然，最终的判别模型仍可鉴别与Query相关或不相关的文档。我们用一个MiniMax目标函数来统一生成模型和判别模型。最终利用强化学习中策略梯度求期望和重参数技巧显式地表达$p_{\theta }(d|q)$