一、题目

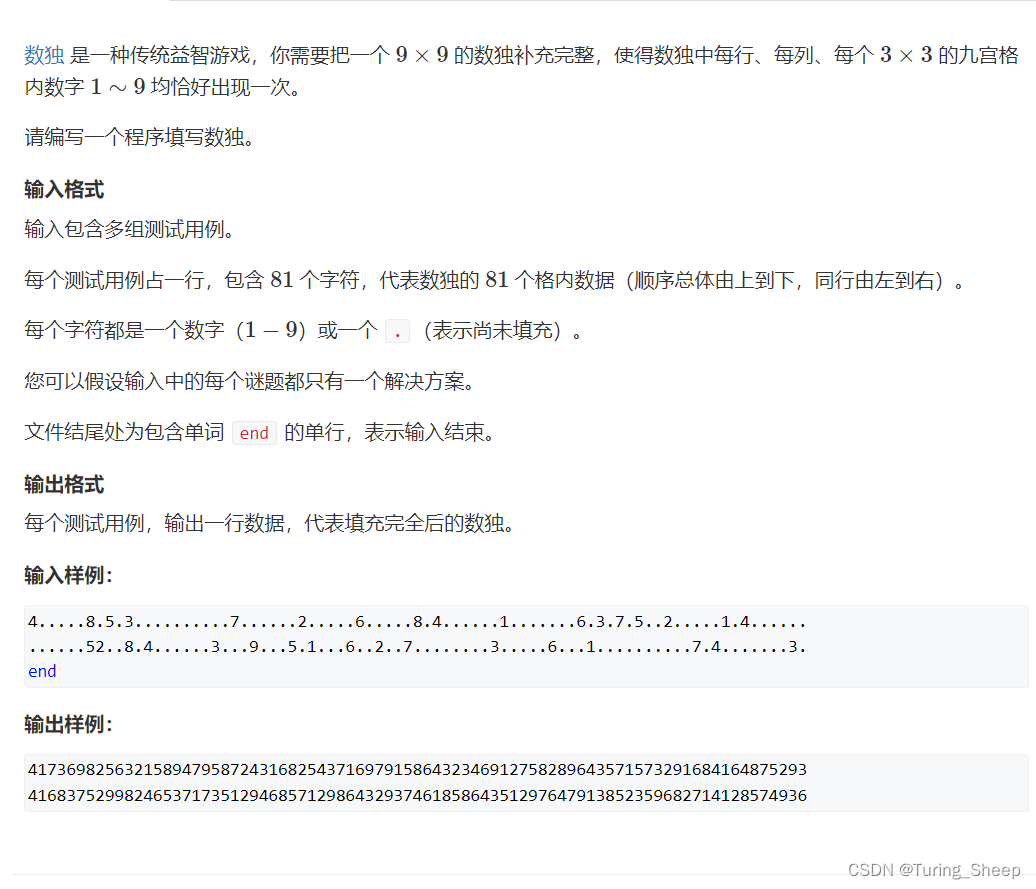
二、分析

1、状态压缩

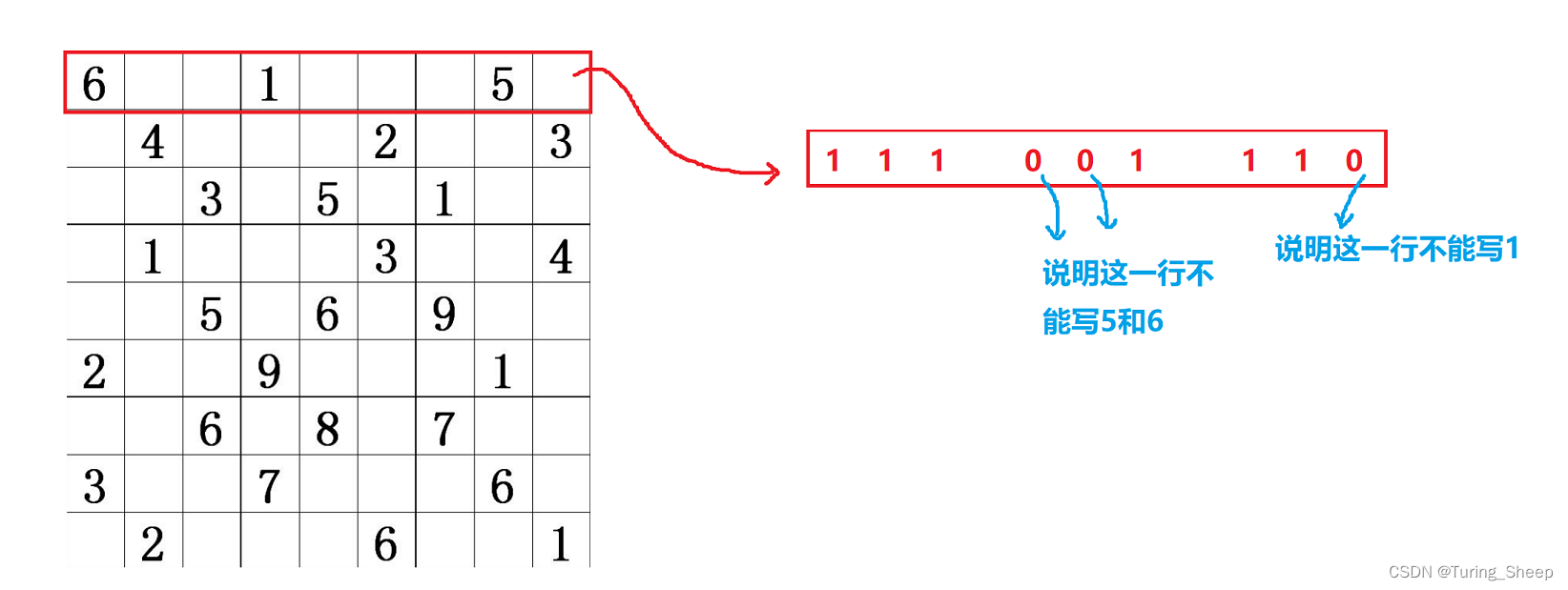
那么如果针对某一个格子而言，我们需要看一看这个格子所在的九宫格，行和列。如果这三种情况下都合法的数字，我们就可以填写。

既然需要三种情况都满足的话，我们就需要看一看这三种请况下所形成的数字中，在对应的位置上，是否是1。

只有三种情况下该位都是1的时候，这一位所代表的数字才有可能填写在该格子上。

此时，我们就可以通过一个式子：$A\&B\&C$ 表示。

2、lowbit函数

（1）函数作用

这个函数的作用是求出一个数的二进制表示中，从右向左数的第一个1。

（2）函数实现

int lowbit(int x)
{
	return x & (-x);
}

比如：

3、DFS思路

DFS的整体思路其实是比较简单的，但是优化起来可能比较麻烦。
整体思路的话，其实就是去枚举每一个需要我们填写的格子可能填写的数字，然后依次向后枚举，直到出现答案。但是这个时间复杂度是非常的恐怖的。

那么我们该如何优化呢？

4、剪枝优化

我们知道对于一棵树而言，它靠近根节点的点，如果子树越多的话，那么整棵树的点就会很多。那么为了减少节点的个数，我们就需要让靠近跟节点的点的子树比较少。那么放到这道题中，就是说我们需要先去枚举那些可填写的合法数字比较少的格子。

这样的话，我们就能对DFS进行一定的优化。

那么在判断一个格子上所填数字是否合法的时候，我们需要去看横行，竖行，九宫格。那么加起来就是27次询问。还是比较低效的，但是根据我们刚刚状态压缩，我们只需要一个式子即可。

这也是其中的一个优化。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 9;
int row[N], col[N], ones[1 << N], cell[3][3];
char str[100];
int ma[1 << N];
int lowbit(int x)
{
	return x & -x;
}

int get(int x, int y)
{
	return row[x] & col[y] & cell[x / 3][y / 3];
}

void init()
{
	for(int i = 0; i < N; i ++ )
		row[i] = col[i] = (1 << N) - 1;

	for(int i = 0; i < 3; i ++ )
		for(int j = 0; j < 3; j ++ )
			cell[i][j] = (1 << N) - 1;
}

void draw(int x, int y, int nums, bool flag)
{
	if(flag)
		str[x * N + y] = '1' + nums;
	else
		str[x * N + y] = '.';
	int v = 1 << nums;
	
	if(!flag)v = -v;

	row[x] -= v;
	col[y] -= v;
	cell[x / 3][y / 3] -= v;
}

bool dfs(int cnt)
{
	if(!cnt)return true;

	int minv = INF;
	int x, y;
	for(int i = 0; i < N; i ++ )
	{
		for(int j = 0; j < N; j ++ )
		{
			if(str[i * N + j] == '.')
			{
				//看看这个格子能写哪几个数字。
				int state = get(i, j);
				//看看能写几个数，我们从情况小的开始枚举，目的是优化。
				if(ones[state] < minv)
				{
					minv = ones[state];
					x = i, y = j;
				}
			}	
		}
	}
	int state = get(x, y);
	for(int i = state; i ; i -= lowbit(i))
	{
		//枚举当前所有可以写的数字
		int t = ma[lowbit(i)];
		//在该位补上合适的数字，并更新行，列，九宫格的状态
		draw(x, y, t, true);
		if(dfs(cnt - 1))return true;
		//复原
		draw(x, y, t, false);
	} 
	return false;
}

void solve()
{
	for(int i = 0; i < N; i ++ )ma[1 << i] = i;//记录1 << i代表的是哪个数字
	for(int i = 0; i < 1 << N; i ++ )
		for(int j = 0; j < N; j ++ )
			ones[i] += i >> j & 1;//记录二进制数字中1的个数

	while(cin >> str, str[0] != 'e')
	{
		init();
		int cnt = 0;//记录需要我们写的格子的数目
		for(int i = 0, k = 0; i < N; i ++ )
			for(int j = 0; j < N; j ++, k ++ )
			{
				if(str[k] != '.')
				{
					int t = str[k] - '1';
					draw(i, j, t, true);
				}
				else
					cnt ++;
			}
		dfs(cnt);
	    cout << str << endl;	
	}

}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	solve();	
}