关系模型简述

形象地说，一个关系就是一个table。

关系模型就是处理table的，它由三个部分组成：

• 描述DB各种数据的基本结构形式；
• 描述table与table之间所可能发生的各种操作；
• 描述这些操作所应遵循的约束条件；

关系模型就是研究：table如何描述，有哪些操作，结果是什么，有哪些约束等。

关系模型的三个要素：

• 基本结构
• 基本操作
• 完整性约束：实体完整性、参照完整性和用户自定义的完整性

关系

域：一组值的集合，这组值具有相同的数据类型。

集合中元素的个数称为域的基数。

笛卡尔积：

元组中的每一个值叫做一个分量。

关系：一组域的笛卡尔积的子集。

关系模式与关系：

• 同一关系模式下，可有很多的关系；
• 关系模式是关系的结构，关系是关系模式在某一时刻的数据；
• 关系模式是稳定的，而关系是某一时刻的值，是随时间可能变化的；

关系的特性：

• 列是同质：即每一列中的分量来自同一域，是同一类型的数据；
• 不同的列可来自同一个域，称其中的每一列为一个属性；
• 关系的任意两个元组不能完全相同；
• 属性不可再分特性：关系第一范式；

候选码/候选键

关系中的一个属性组，其值能唯一标识一个元组，若从该属性组中去掉任何一个属性，他就不具有这一性质了，这样的属性组称作候选码。

主码/主键

当有多个候选码时，可以选定一个作为主码。

主属性：包含在任何一个候选码中的属性被称作主属性；

非主属性：而其他属性被称作非主属性。

所有属性构成这个关系的候选码，称为全码。

外码/外键

关系R中的一个属性组，它不是R的候选码，但它与另一个关系S的候选码相对应，则称这个属性组为R的外码。

关系模型的完整性

实体完整性：关系的主码中的属性值不能为空值（不知道或无意义的值）；

参照完整性：如果关系R1的某个元组t1参照了关系R2的某个元组t2，则t2必须存在；

• 空值，表示尚未分配；
• 非空值则必须时相应元组中存在的值；

用户自定义完整性：用户针对具体的应用环境定义的完整性约束条件。

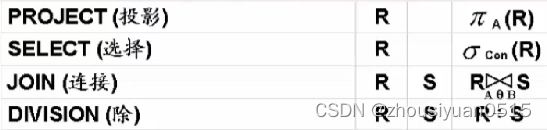
关系代数

关系代数基于集合，提供了一系列的关系代数操作：并、差、笛卡尔积（广义积）、选择、投影和更名等基本操作，以及交、连接和关系除等扩展操作，是一种集合思维的操作语言。

关系代数操作以一个或多个关系为输入，结果是一个新的关系。

集合操作

纯关系操作

 

并相容性

某些关系代数操作，如并、差、交等，需满足并相容性。

参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意义关联性。

• 关系R与关系S的属性数目必须相同；
• 属性的域也相同；

并：

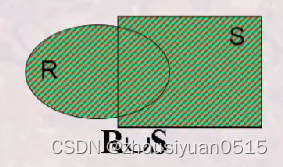
差：

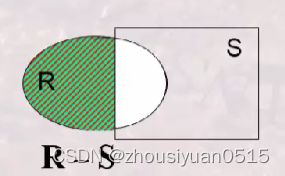
笛卡尔积：

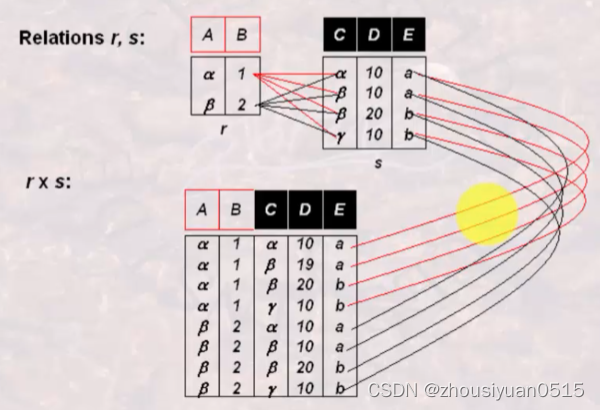
选择：给定一个关系R，同时给定一个选择的条件，选择运算结果也是一个关系。

投影：从关系R中选出包含在A中的列构成。

交：

θ-连接：给定关系R和关系S，R域S的θ连接运算结果也是一个关系，它由关系R域关系S的笛卡尔积中，选取属性A域S中属性B这几件满足θ条件的元组构成。

自然连接：给定关系R和关系S，R与S的自然连接运算结果也是一个关系，它由关系R和关系S的笛卡尔积中选取相同属性组B上值相等的元组所构成。

除：经常用于求解查询所有的/全部的问题

外连接：两个关系R与S连接时，如果找不到相匹配的元组，将该元组和全为空值的元组形成连接，放在结果关系中。

关系演算

关系元组演算

关系演算是以梳理逻辑中的谓词演算为基础的，关系演算是描述关系运算的另一种思维方式。

根据谓词变量的不同，可分为关系元组演算和关系域演算：

• 关系元组演算是以元组变量作为谓词变量的基本对象；
• 关系域演算是以域变量作为谓词变量的基本对象；

关系元组演算公式的基本形式：{ t | P(t) }

上式表示：所有使谓词P为真的元组t的集合；

• t是元组变量
• t∈r表示元组t在关系r中
• t[A]表示元组t的分量，即t在属性A上的值
• P是与谓词逻辑相似的公式，P(t)表示以元组t为变量的公式

这个公式可以递归地构造。

用元组演算实现关系代数

关系域演算

关系域演算公式的基本形式：{ <x1, x2, ..., xn> | P(x1, x2, ..., xn) }

域演算语言QBE

不想写了

 关系运算的安全性

• 关系代数是一种集合运算，是安全的：集合本身是有限的，有限元素集合的有限次运算依旧是有限的；
• 关系演算不一定是安全的；
• 需要对关系演算施加约束条件，即任何公式都在一个集合范围内操作，而不是无限范围内操作，才能保证其安全性；