题目描述

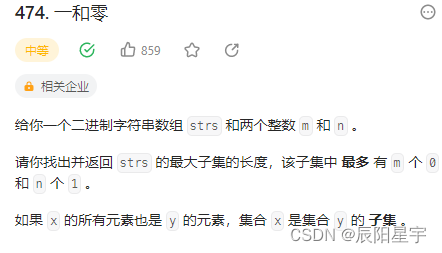
在这里插入图片描述

原题链接：474. 一和零

解题思路

（1）三维数组

本题是要在已有的字符串中，找到给定的m个0和n个1，组出最大的子集。将字符串集合中的各个字符串看作物品，m个0和n个1看作背包的重量，则该题就可以转化为01背包问题，其中m个0和n个1，可看作一个背包中两个不同维度的表示。

动态规划五步曲：
（1）dp[i][j][k]的含义： 选取到第i个字符串时，使用j个0和n个1，可组成的最大子集长度。
（2）递推公式： dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - zeros][k - ones] + 1)，其中zeros和ones分别表示当前字符中0的数量和1的数量。该递推公式的意思是在不选择第i个字符串和选择第i个字符串，看哪个情况可组成最大子集。
（3）dp[i][j][k]初始化： dp[i][0][0] = 0，0和1的数量为0时，不能组成任何非空字符。
（4）遍历顺序： 先遍历字符串，再遍历1的个数，最后遍历0的个数，内层从小到大遍历。
（5）举例：（省略）

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int dp[601][101][101] = {0};
        // 先对字符串进行遍历
        for(int i = 1; i <= strs.size(); i++) {
            // 统计当前字符中零和一的数量
            int zeros = 0, ones = 0;
            for(char ch : strs[i - 1]) {
                if(ch == '0')       zeros++;
                else                ones++;                
            }
            // 再对背包中0维度和1维度进行遍历
            for(int j = 0; j <= m; j++) {
                for(int k = 0; k <= n; k++) {
                    // 0和1的数量不够组成当前字符，则保持原样
                    if(j < zeros || k < ones)           dp[i][j][k] = dp[i - 1][j][k];
                    // 0和1的数量狗组成当前字符，则寻找最大子集长度
                    else if(j >= zeros && k >= ones)    dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - zeros][k - ones] + 1);
                }
            }
        }
        return dp[strs.size()][m][n];
    }
};

（2）优化二维滚动数组

因为一个字符串代表一个物品，其重量为1，因此可以省去该数组维度，将三维数组优化为二维滚动数组。

对“背包”遍历时候从大到小遍历，可以保证max中式子等价于i-1时的情况。 如果是从小到大遍历的话，虽然第一次计算的结果会使i-1时的情况，但后续继续遍历时，由于j - zeros和k - ones可能会出现之前在i时遍历过程中已经被更新的情况，导致重复计数。而如果从大到小遍历的话，就可以保证每次遍历时都是按照i-1时的情况计算，并且在后续遍历时不会出现重复计数。

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int dp[101][101] = {0};
        for(int i = 1; i <= strs.size(); i++) {
            int zeros = 0, ones = 0;
            for(char ch : strs[i - 1]) {
                if(ch == '0')       zeros++;
                else                ones++;                
            }
            // 从大到小遍历，可以保证max里式子，等价于i-1时情况
            for(int j = m; j >= zeros; j--) {
                for(int k = n; k >= ones; k--) {
                    dp[j][k] = max(dp[j][k], dp[j - zeros][k - ones] + 1);
                }
            }
        }
        return dp[m][n];
    }
};