文章全文首发：码农的科研笔记（公众号）

---

原文：https://arxiv.org/abs/2111.01013

1 动机

位置推荐定义为推荐地理位置给用户，现有推荐无法无法很好的建模地理位置属性，这导致推荐结果是次优的。同时作者希望消除 POI (Point-of-Interest) 推荐中的geographical bias (即用户所选择的场所, 可能不是纯兴趣导向的, 而很大程度受距离远近的影响).

2 方法

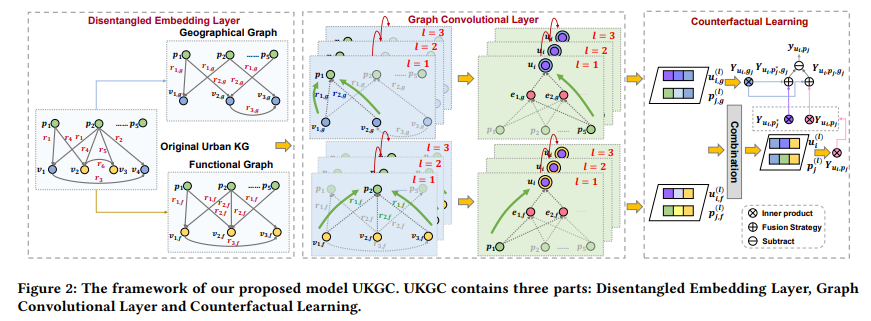
首先构建城市知识图(UrbanKG) （具有兴趣点的地理信息和功能信息）。之后在两个子图上进行信息传播，以获取兴趣点和用户的表示。然后，我们通过反事实学习来融合两部分表征（利用图网络提取特征, 利用 TIE (Total Indirect Effect) 来消除 geographical bias ）以获得最终预测。

• Urban Knowledge Graph Construction：上述模型开始是一个有向图结构，其表示为下图所示。这个图节点类型包含7种（例如：business area、region、brands）和16种关系（例如 locateAt、NearBy）。例如下面 (Apple Store East Nanjing Road, BrandOf, Apple) 信息，实际表示的是POI ‘Apple Store East Nanjing Road’ 的 brand 是 entity ‘Apple’。其中关系又主要分为 geographical (地理上的关系) 和 functional (功能上的关系) 两类。

  

• Disentangled Embedding Layer：将原始图，分解为 geographical and functional attributes 这两个方面的图数据；

• Graph Convolutional Layer：得到disentangled representations of geographical and functional attributes用的方法；

• Counterfactual Learning：反事实推理来减轻地理位置偏置，从而更好的实现POI推荐。

2.1【因果图】

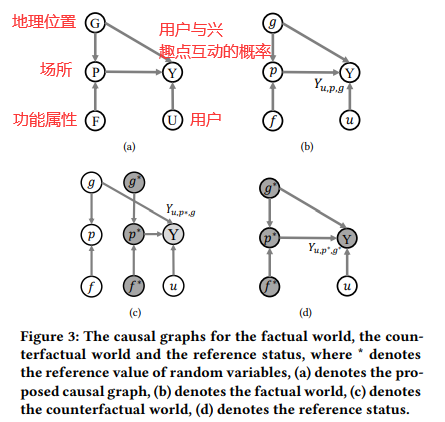
作者希望通过估计TIE从而进行推荐
$${\hat{y}}_{u_i,p_j}=TIE=TE-TDE=Y_{u_i,p_j,g_j}-Y_{u_i,p_j^{\ast },g_j}.$$
其中具体计算作者定义为
$$\begin{array}{l}{\mathrm{Y}}_{u_i,p_j,g_j}=f\left({\mathrm{Y}}_{u_i,p_j},{\mathrm{Y}}_{u_i,g_j}\right)\\ {\mathrm{Y}}_{u_i,p_j^{\ast },g_j}=f\left({\mathrm{Y}}_{u_i,p_j^{\ast }},{\mathrm{Y}}_{u_i,g_j}\right)\end{array}$$
其中 $f(\cdot )$ 函数定义为下面：
$$f\left({\mathrm{Y}}_{u_i,p_j},{\mathrm{Y}}_{u_i,g_j}\right)={\mathrm{Y}}_{u_i,p_j}\ast \tanh \left({\mathrm{Y}}_{u_i,g_j}\right).$$
上式中进一步定义有：

$$\begin{array}{c}{\mathrm{Y}}_{u_i,p_j}={\mathbf{u}}_i^T{\mathbf{p}}_j,{\mathrm{Y}}_{u_i,g_j}={\mathbf{u}}_{i,g}^T{\mathbf{p}}_{j,g},\\ {\mathrm{Y}}_{u_i,p_j^{\ast }}=\mathbb{E}\left({\mathrm{Y}}_{u_i,P}\right)=\frac{1}{|\mathcal{P}|}{\sum }_{p_t\in \mathcal{P}}{\mathrm{Y}}_{u_i,p_t}\end{array}$$
where $\mathcal{P}$ denotes the set of POIs and $|P|$ is the cardinality of the set $|P|$ .

2.2【损失定义】

$$\begin{array}{r}\mathcal{L}={\mathcal{L}}_F+{\lambda }_1({\mathcal{L}}_{\mathrm{IND}g}+{\mathcal{L}}_{\mathrm{IND}f})+{\lambda }_2\Vert \Theta {\Vert }_2\alpha \left({\mathcal{L}}_C+{\lambda }_2{\Vert {\Theta }_g\Vert }_2\right),\end{array}$$

• 为了优化真实场景下 $Y_{u_i,p_j,g_j}$，利用BPR loss，其中 O = { ( u i , p j , p k ) ∣ ( u i , p j ) ∈ O + , ( u i , p k ) ∈ O − } O=\left\{\left(u_{i}, p_{j}, p_{k}\right) \mid\left(u_{i}, p_{j}\right) \in O^{+},\left(u_{i}, p_{k}\right) \in O^{-}\right\} O={(ui​,pj​,pk​)∣(ui​,pj​)∈O+,(ui​,pk​)∈O−} 是训练数据，其中 $O^{+} $表示正交互样本，$O^{-} $表示负交互样本。
  $${\mathcal{L}}_F=\sum _{(u_i,p_j,p_k)\in \mathcal{O}}-\ln \sigma (Y_{u_i,p_j}-Y_{u_i,p_k}),$$

• 为了在反事实场景下获得更好的 $Y_{u_i,p_j^{\ast },g_j}$，其中$ \mathrm{Y}{u{i}, p_{j}^{*}}=\mathbb{E}\left(\mathrm{Y}{u{i}, P}\right)$，作者也是采用 BPR loss进行区分 ${\mathrm{Y}}_{u_i,g_j}$ 和 ${\mathrm{Y}}_{u_i,g_k}$
  $${\mathcal{L}}_C=\sum _{\left(u_i,g_j,g_k\right)\in O}-\ln \sigma \left({\mathrm{Y}}_{u_i,g_j}-{\mathrm{Y}}_{u_i,g_k}\right)$$

• ${\mathcal{L}}_{\mathrm{IND}}$是distance correlation确保用户意图的独立性 携带尽可能多的信息。

3 总结

图谱的构建是文章的亮点，通过两个方面的信息进行建模，之后运用反事实理论得到更好的推荐结果（推荐系统是反应$P\to Y$，而我们建模还是需要更好的反应各个因素对 $Y$ 的影响）。