E-阿宁的生成树_2023牛客寒假算法基础集训营6 (nowcoder.com)

开始慢慢补牛牛的题

题意：

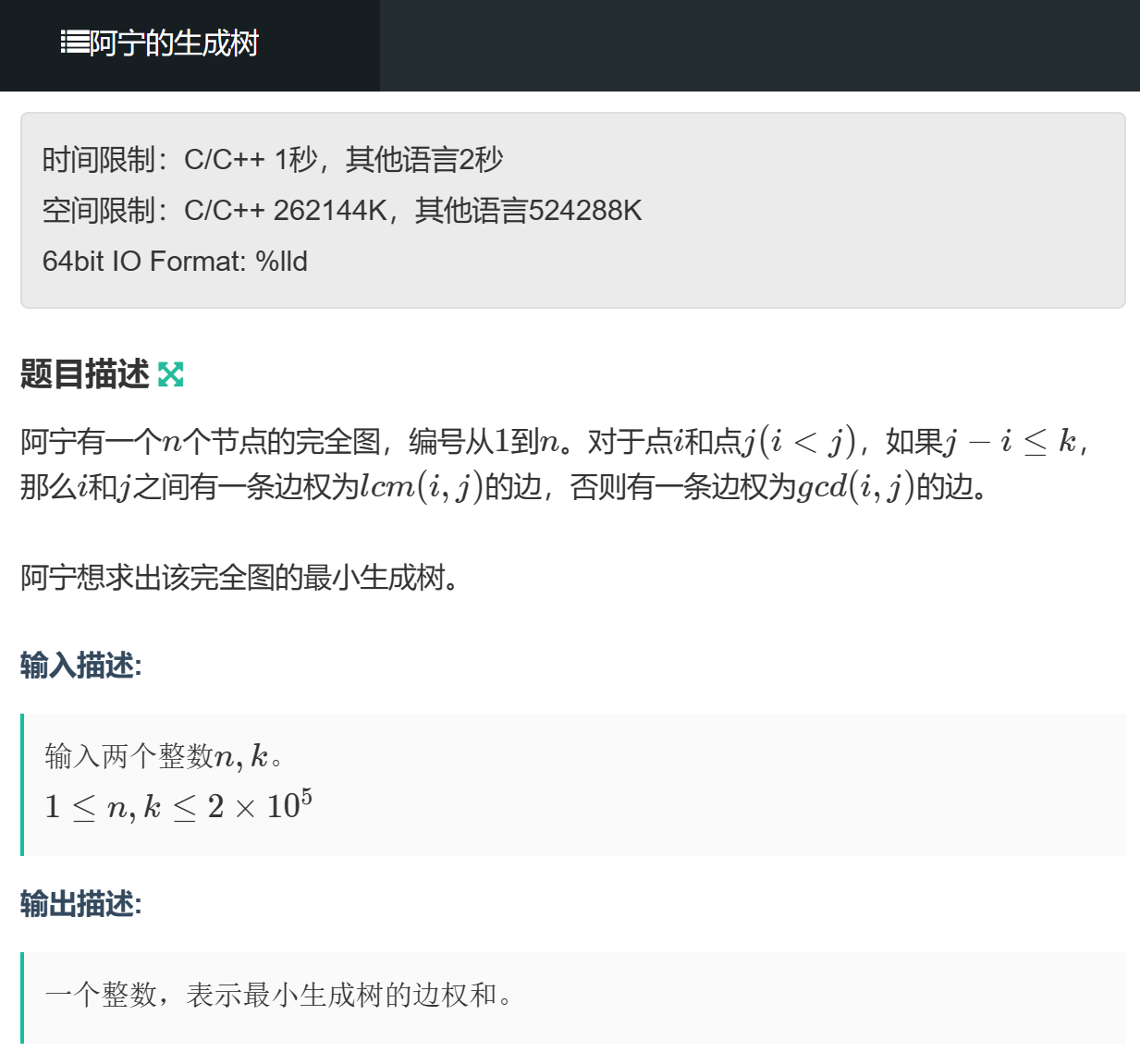
最小生成树+质数距离

思路：

最小生成树一共就两种算法，我们考虑Prim的过程

初始连通块是1，然后考虑拿1和其他的结点连边

当j-i<=k时边权是gcd，j-i>k时边权是lcm

考虑j-1>k的点

即j>k+1

即j>=k+2

显然，对于[k+2,n]的结点来说，边权都是gcd(1,i)，都为1

对于[2,k+2)的点，如果是和结点1连边，边权就是i，因此对于这些点的边权最多就是i

但是如果区间[2,k+2]的点和附近区间k的点连gcd的边，边权可能会变小

这里考虑暴力，用已经松弛的[k+2,n]的结点去松弛区间[2,k+2)的点

如果遍历到的已经松弛的结点是质数，那么边权一定为1，所以可以break

小trick:1e8以内的质数距离最多200，因此时间复杂度是O(n*200)，不会超时

#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;



int n,k,len=0;
int d[mxn],prime[mxn],vis[mxn];
void p_init(int n){
    for(int i=2;i<=n;i++){
        if(!vis[i]) prime[++len]=i;
        for(int j=1;i<=n/prime[j];j++){
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}
void solve(){
    cin>>n>>k;
    for(int i=2;i<=n;i++) d[i]=i;
    for(int i=1+k+1;i<=n;i++) d[i]=1;
    for(int i=2;i<1+k+1;i++){
        for(int j=i+k+1;j<=n;j++){
            d[i]=min(d[i],__gcd(i,j));
            if(!vis[j]) break;
        }
    }
    int ans=0;
    for(int i=2;i<=n;i++) ans+=d[i];
    cout<<ans<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    p_init(2e5);
    while(__--)solve();return 0;
}