Java之动态规划之子序列问题

news2024/9/24 20:31:37

目录

0.动态规划问题

一.最长递增子序列

1.题目描述

2.问题分析

3.代码实现

二.最长递增子序列

1.题目描述

2.问题分析

3.代码实现

三.最长重复子数组

1.题目描述

2.问题分析

3.代码实现

4.代码的优化(滚动数组)

四.最长公共子序列

1.题目描述

2.问题分析

3.代码实现

4.代码优化(滚动数组)

五.不相交的线

1.题目描述

2.问题分析

3.代码实现

4.代码优化(滚动数组)

六.最大子数组和

1.题目描述

2.问题分析

3.代码实现

七.判断子序列

1.题目描述

2.问题分析

3.代码实现

4.双指针代码实现

0.动态规划问题

动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题,进行解决，从而一步步获取最优解的处理算法

动态规划对于解决最优子结构啊和重叠子问题等问题时候,有着很好的应用

对于动态规划问题,大致可以分为以下几步:

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

一.最长递增子序列

1.题目描述

 给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

力扣:力扣

2.问题分析

这一题首先要理解子序列问题,子序列不一定是连续一段的数组(子数组),只需要它的序列是递增的即可(例如index=0,2,3)

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

本题的dp数组定义不是根据题目直接来进行定义,需要根据题意进行变通定义

dp[i]数组的含义:以nums[i]为结尾的最长递增子序列长度为dp[i]

注意:这里一定要以nums[i]为结尾,不可去除这个元素

2.确定递推公式

位置i的元素最长的递增子序列等于位置从0到j-1位置上最长递增子序列+1的最大值

递推公式:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意:这里dp[i] = max(dp[i], dp[j] + 1)是为了取dp[i]的最大值,并不是dp[i]和dp[j] + 1比较

注意:这里它的最大值并不一定出现在dp[nums.length-1]的位置,如何最后一个数字比前边的都小,而dp数组的定义必须以nums[i]为结尾,所有此时dp[i]的值可能为1,因为应该取dp数组元素的最大值

3.dp数组如何初始化

由题意可知,无论前边的nums[j]是否比nums[i]大,总有一个元素满足递增序列,就是它本身自己,所有每一个dp[i]都应该初始化为1

4.确定遍历顺序

因为最长递增子序列是从前到后递增,所以我们也应该从左到右进行遍历

5.举例推导dp数组

对nums = [10,9,2,5,3,7,101,18]进行推导

i01234567
dp[i]11122344

它的最长的递增序列是{2,3,7,101}或者{2,3,7,18}

3.代码实现

    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        int max = 1;
        Arrays.fill(dp, 1);
        for (int i = 1; i < nums.length; ++i) {
            for (int j = 0; j < i; ++j) {
                if (nums[i] > nums[j])
                    dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            max = Math.max(max, dp[i]);
        }

        return max;

    }

二.最长递增子序列

1.题目描述

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

力扣:力扣

2.问题分析

这里明确说了是连续的子序列,所以序列值应该是连在一起的,如:index=1,2,3

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

dp[i]数组的含义是:以nums[i]为结尾的连续递增子序列的最大值

2.确定递推公式

这一题和上一题明显的不同就是连续与否,上一题如何nums[i]<nums[i-1],那么它的递增还有可能和i-1之前的数据构成递增序列,这一题,因为存在一个连续,所以如果nums[i]<nums[i-1],那么他肯定是不能构成连续递增序列了,因此这时dp[i]=1;如果nums[i]>nums[i-1],说明与前边的元素构成连续递增序列,因此dp[i]=dp[i-1]+1;

递推公式为:if (nums[i] > nums[i - 1])     dp[i] = dp[i - 1] + 1;

注意:这一题仍然需要dp数组中的最大值,原因和上一题一样

3.dp数组如何初始化

和上一题一样,所有的初始化为1

4.确定遍历顺序

和上一题一样,从左到右,但这一题只需要一层循环

5.举例推导dp数组

推导nums = [1,3,5,4,7]

i01234
dp[i]12312

 最长连续递增序列为:{1,3,5}

3.代码实现

    public static int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        int max = 0;
        Arrays.fill(dp, 1);
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] > nums[i - 1])
                dp[i] = dp[i - 1] + 1;
            max = Math.max(i, dp[i]);
        }
        return max;

    }

三.最长重复子数组

1.题目描述

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

力扣:力扣

2.问题分析

题目中说的就是子数组就是连续子序列

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

因为这一题是两个数组,所以最好定义为二维数组

dp[i][j]的含义是:以nums1[i]结尾的A和以nums2[j]结尾的B,最长的公共子数组的长度是dp[i][j]

2.确定递推公式

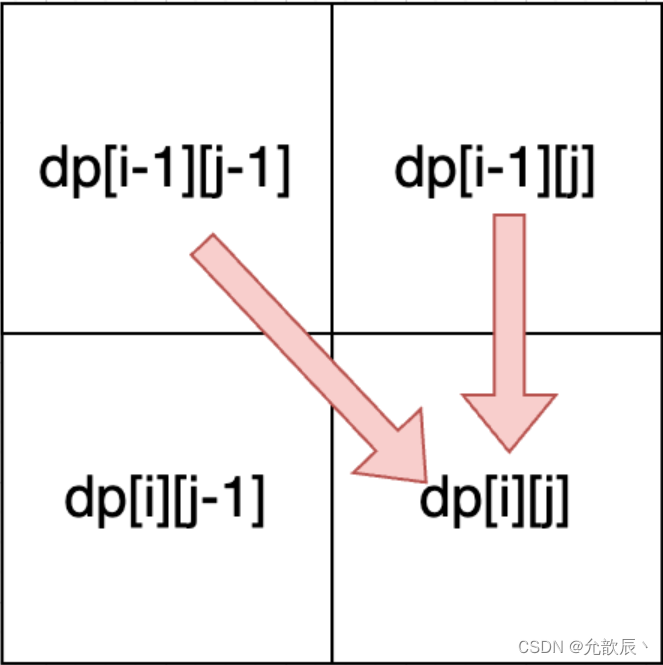
子数组和连续子序列的含义是一样的,如果nums1[i]==nums2[j],此时只需要知道前边的最长的公共子数组的最大长度,就是dp[i-1][j-1](含义是以nums1[i-1]结尾的A和以nums2[j-1]结尾的B,最长的公共子数组的长度),此时+1便等于dp[i][j],如果不相等的话,这个时候公共子数组长度显然为0,不需要赋值

所以递推公式为:if (nums1[i] == nums2[j])  dp[i][j] = dp[i - 1][j - 1] + 1;

注意:这一题仍然需要dp数组中的最大值,原因和上一题一样

3.dp数组如何初始化

由递推公式可以知道由斜上方的元素推导出来的,所以至少要对第一行和第一列进行初始化赋值

具体的初始化代码如下: 

        //对第一列进行初始化
        for (int i = 0; i < nums1.length; i++) {
            if (nums1[i] == nums2[0])
                dp[i][0] = 1;
            result = Math.max(result, dp[i][0]);
        }
        //对第一行进行初始化
        for (int j = 0; j < nums2.length; j++) {
            if (nums1[0] == nums2[j])
                dp[0][j] = 1;
            result = Math.max(result, dp[0][j]);
        }

4.确定遍历顺序

由递推公式可以看出,是由从上到下,从左到右进行遍历的

5.举例推导dp数组

对nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]进行推倒后的dp数组

[0, 0, 1, 0, 0]
[0, 1, 0, 0, 0]
[1, 0, 0, 0, 0]
[0, 2, 0, 0, 0]
[0, 0, 3, 0, 0]

3.代码实现

    public  int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length][nums2.length];
        int result = 0;
        //对第一列进行初始化
        for (int i = 0; i < nums1.length; i++) {
            if (nums1[i] == nums2[0])
                dp[i][0] = 1;
            result = Math.max(result, dp[i][0]);
        }
        //对第一行进行初始化
        for (int j = 0; j < nums2.length; j++) {
            if (nums1[0] == nums2[j])
                dp[0][j] = 1;
            result = Math.max(result, dp[0][j]);
        }
        for (int i = 1; i < nums1.length; i++) {
            for (int j = 1; j < nums2.length; j++) {
                if (nums1[i] == nums2[j]) { // 防止 i-1 出现负数
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                result = Math.max(result, dp[i][j]);
            }
        }

        return result;

    }

也可以进行这样设置 dp数组:以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j],这样的代码实现为  dp[i][0]和dp[0][j]没有意义,全部赋值为0   (推荐)

 public int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        int res = 0;
        for (int i = 1; i <= nums1.length; ++i) {
            for (int j = 1; j <= nums2.length; ++j) {
                if (nums1[i - 1] == nums2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                res = Math.max(res, dp[i][j]);
            }
        }
        return res;


    }

4.代码的优化(滚动数组)

这样其实和01背包的二维数组优化成滚动数组一个思路,都是长度为nums2.length长的数组,然后第一个从左到右遍历,第二个从右到左遍历,为了不影响其他数据使用成为第二次推导出的数据

01背包指路:Java之动态规划的背包问题_允歆辰丶的博客-CSDN博客

第一个dp数组的含义:以nums2[j]为结尾的dp[j]:代码实现

  public int findLength4(int[] nums1, int[] nums2) {
        int[] dp = new int[nums2.length];
        int result = 0;

        //对第一行进行初始化
        for (int j = 0; j < nums2.length; j++) {
            if (nums1[0] == nums2[j])
                dp[j] = 1;
            result = Math.max(result, dp[j]);
        }
        System.out.println(Arrays.toString(dp));
        for (int i = 1; i < nums1.length; i++) {
            for (int j = nums2.length - 1; j >= 0; --j) {
                if (nums1[i] == nums2[j]) { // 防止 i-1 出现负数
                    if (j == 0) {
                        dp[j] = 1;
                        continue;
                    }

                    dp[j] = dp[j - 1] + 1;
                    result = Math.max(result, dp[j]);
                } else {
                    dp[j] = 0;
                }
            }
            System.out.println(Arrays.toString(dp));
        }

        return result;


    }

第二种dp数组的含义:以nums2[j-1]为结尾的dp[j]:代码实现(推荐)

    public int findLength2(int[] nums1, int[] nums2) {
        int[] dp = new int[nums1.length + 1];
        int res = 0;
        for (int i = 1; i <= nums1.length; ++i) {
            for (int j = nums2.length; j >= 1; --j) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else
                    dp[j] = 0;
                res = Math.max(dp[j], res);
            }
        }
        return res;


    }

四.最长公共子序列

1.题目描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

力扣:力扣

2.问题分析

子序列,显然是不连续的

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

dp[i][j]的含义:长度为[0,i-1]的text1和长度为[0,j-1]的text2最最长公共子序列的长度为dp[i][j]

注意:这里不一定一定以text[i-1]结尾,只需要在[0,i-1]任意子字符串最长即可

2.确定递推公式

主要就是两种情况,一种就是text1.charAt(i-1)==text2.charAt(j-1);另一种是不相同

当相等的情况,很显然就是两个字符串长度各-1的最长公共子序列的长度+1,就是            dp[i][j]=dp[i-1][j-1]+1      例如(aab和bab,dp[2][2]=1,dp[3][3]=2)

当不相等的时候,就是text1[0,i-2]的text2和长度为[0,j-1]和text1[0,i-1]的text2和长度为[0,j-2]的最大值作为dp[i][j]的值

dp[i][j]=max(dp[i][j-1],dp[i-1][j])

                if (text1.charAt(i - 1) == text2.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }

3.dp数组如何初始化

因为dp[i][0]和dp[0][j]没有意义,所以初始化为0

,4.确定遍历顺序

 由推导公式可以知道,遍历顺序是从左到右,从上到下的

5.举例推导dp数组

对于text1 = "abcde", text2 = "ace" 进行推导

[0, 0, 0, 0]
[0, 1, 1, 1]
[0, 1, 1, 1]
[0, 1, 2, 2]
[0, 1, 2, 2]
[0, 1, 2, 3]

最长公共子序列是 "ace" ，它的长度为 3 。

3.代码实现

    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];

        for (int i = 1; i <= text1.length(); ++i) {
            for (int j = 1; j <= text2.length(); ++j) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];

    }

4.代码优化(滚动数组)

    public int longestCommonSubsequence2(String text1, String text2) {
        int[] dp = new int[text2.length() + 1];

        for (int i = 1; i <= text1.length(); ++i) {
            int pre=dp[0];
            for (int j = 1; j <= text2.length(); ++j) {
                int cur = dp[j];
                if (text1.charAt(i - 1) == text2.charAt(j - 1))
                    dp[j] = pre + 1;
                else {
                    dp[j] = Math.max(cur, dp[j - 1]);
                }
                pre=cur;
            }
        }

        return dp[text2.length()];

    }

五.不相交的线

1.题目描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

  •  nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

力扣:力扣

2.问题分析

这一题看样子题目意思改变了很多,其实和上一题字符串的意思是一样的,它规定是连线不可以相交的,其实意思就是i与j的相对位置是不可以改变的,比如nums1[i]==nums[j]了,那么这个时候你只能继续向后遍历,不可以反过来遍历,例如(nums1[i+1]==nums[j-1])这样是不行的,只能接着往后面相加,这样就和上一题的意思是一模一样的了

 例如这一题:

5.举例推导dp数组

对于nums1 = [1,4,2], nums2 = [1,2,4]推导

[0, 1, 1, 1]
[0, 1, 1, 2]
[0, 1, 2, 2]

nums1[1]=4 到 nums2[2]=4,所以最多画两条线

3.代码实现

  public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        for (int i = 1; i <= nums1.length; ++i) {
            for (int j = 1; j <= nums2.length; ++j) {
                if (nums1[i - 1] == nums2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }

            }

        }
        return dp[nums1.length][nums2.length];


    }

4.代码优化(滚动数组)

    public static int maxUncrossedLines2(int[] nums1, int[] nums2) {
        int[] dp = new int[nums2.length + 1];
        for (int i = 1; i <= nums1.length; ++i) {
            int pre = dp[0];
            for (int j = 1; j <= nums2.length; ++j) {
                int cur = dp[j];
                if (nums1[i - 1] == nums2[j - 1])
                    dp[j] = pre + 1;
                else {
                    dp[j] = Math.max(cur, dp[j - 1]);
                }
                pre = cur;

            }

        }

        return dp[nums2.length];
        
    }

六.最大子数组和

1.题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

力扣:力扣

2.问题分析

最大子数组说明是连续的

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

dp[i]的含义是:以nums[i]结尾的子数组的最大和是dp[i]

2.确定递推公式

存在两种情况,一种就是i前边的最大子数组和加上nums[i],一种就是从只有nums[i],因为dp[i-1]可能存在已经是负值的情况,如果再加上nums[i],只会使值变小,这个时候从新从nums[i]开始更好,如果前边已经是正数了,加上nums[i](可能使dp[i-1]>dp[i],因为nums[i]可能为负数,因为dp数组定义的缘故,必须加入)

所以递推公式为:dp[i]=max(dp[i-1]+nums[i],nums[i]);

3.dp数组如何初始化

由递推公式可知,只需要初始化dp[0],因为子数组至少有一个值,所以dp[0]=nums[0];

4.确定遍历顺序

由递推公式可知,从左到右进行遍历

5.举例推导dp数组

对[-2,1,-3,4,-1,2,1,-5,4]进行推导

i012345678
dp[i]-21-2435615

3.代码实现

    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        int res=nums[0];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; ++i) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            res=Math.max(res,dp[i]);
        }
        return res;

    }

七.判断子序列

1.题目描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

力扣:力扣

2.问题分析

子序列:是不连续的问题,这一题其实和四.最长公共子序列差不多的问题,略有不同之后说明

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

dp[i][j]的含义是:从[0,i-1]的子字符串s和从[0,j-1]的子字符串t,相同子序列的长度是dp[i][j]

注意:这里和第四题的dp数组还是有一点区别的

2.确定递推公式

主要也是分为两种情况,一种就是当s.charAt[i-1]==t.charAt[j-1],这个时候dp[i][j] = dp[i - 1][j - 1] + 1.这个时候相当于在i位置上的字符在t中找了                                                                                 第二种情况:s.charAt[i-1]!=t.charAt[j-1],这个时候就不能和第四题一样了,因为这一题是要找s是否为 t 的子序列,s数组如果你找到了几个字符在t中,你这个时候是不可以dp[i-1][j],这样就是s向前找,但是s还不可以删除的,例如s="abc"c,t="aacbc",这个时候第一个a==a,然后b!=a,但这个时候你不可以使s字符串找到前边的a.

所以推导公式为:

if (s.charAt(i - 1) == t.charAt(j - 1))
    dp[i][j] = dp[i - 1][j - 1] + 1;
else {
    dp[i][j] = dp[i][j - 1];
}

3.dp数组如何初始化

由递推公式可知,dp[0][j]和dp[i][0]没有意义,初始化为0

4.确定遍历顺序

由递推公式可知,从前到后,从上到下

5.举例推导dp数组

对s = "abc", t = "ahbgdc"进行推导

[0, 1, 1, 1, 1, 1, 1]
[0, 0, 0, 2, 2, 2, 2]
[0, 0, 0, 0, 0, 0, 3]

3.代码实现

    public boolean isSubsequence(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 1; i <= s.length(); ++i) {
            for (int j = 1; j <= t.length(); ++j) {
                if (s.charAt(i - 1) == t.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else {
                    dp[i][j] = dp[i][j - 1];
                }

            }
        }
      return dp[s.length()][t.length()]==s.length();
    }

4.双指针代码实现

当然,这一题也可以选择使用双指针来解决,代码实现

    public boolean isSubsequence2(String s, String t) {
        int j = 0;
        for (int i = 0; i < s.length(); ++i) {
            while (j < t.length() && s.charAt(i) != t.charAt(j)) {
                j++;
            }
            j++;
        }
        return j <= t.length();
    }

八.不同的子序列

1.题目描述

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

力扣:力扣

2.问题分析

这里和第七题有相似之处,但还是有一定的区别

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

dp[i][j]的含义是:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]

2.确定递推公式

其实这一题和上一题一样,dp[i][j]还是分两种情况

一种:当s.charAt[i-1]==t.charAt[j-1],此时dp[i][j]由两部分组成

当t.charAt[j-1]来进行匹配出现次数的时候,这一部分为dp[i-1][j-1]

当t.charAt[j-1]不是匹配出现次数的时候,这一部分为dp[i-1][j]

另一种:当s.charAt[i-1]!=t.charAt[j-1],这个时候只有t.charAt[j-1]不是匹配出现次数的时候为dp[i-1][j]

                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }

 

3.dp数组如何初始化

首先我们需要先回顾一下dp数组的含义

dp[i][0]的含义是t数组为空的时候,以i-1结尾的s出现在t中的个数,因为t为空,这个时候赋值为1

dp[0][j]的含义是s数组为空,s出现在以j-1结尾的t中的个数,这个时候赋值为0

        for (int i = 0; i <= s.length(); ++i) {
            dp[i][0] = 1;
        }

4.确定遍历顺序

由递推公式可知,从前到后,从上到下

5.举例推导dp数组

对s = "rabbbit", t = "rabbit"进行推导

[1, 0, 0, 0, 0, 0, 0]
[1, 1, 0, 0, 0, 0, 0]
[1, 1, 1, 0, 0, 0, 0]
[1, 1, 1, 1, 0, 0, 0]
[1, 1, 1, 2, 1, 0, 0]
[1, 1, 1, 3, 3, 0, 0]
[1, 1, 1, 3, 3, 3, 0]
[1, 1, 1, 3, 3, 3, 3]

 

3.代码实现

    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 0; i <= s.length(); ++i) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= s.length(); ++i) {
            for (int j = 1; j <= t.length(); ++j) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }

            }
        }
        return dp[s.length()][t.length()];

    }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/340650.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C语言学习笔记(五)：数组的使用

C语言学习笔记(五)：数组的使用

数组的定义 数组是一组有序数据的集合。数组中各数据的排列是有一定规律的&#xff0c;下标代表数据在数组中的序号。 用数组名和下标即可唯一地确定数组中的元素。 数组中的每一个元素都属于同一个数据类型。 一维数组 定义与引用 int a[10] {0,1,2,3,4,5,6,7,8&#xf…
阅读更多...
Matlab绘制隐函数总结-二维和三维

Matlab绘制隐函数总结-二维和三维

1.二维隐函数 二维隐函数满足f(x,y)0f(x,y)0f(x,y)0&#xff0c;这里无法得到yf(x)yf(x)yf(x)的形式。不能通过普通函数绘制。 我们要关注的是使用fplot函数和fimplicit函数。 第1种情况&#xff1a;基本隐函数 基本的隐函数形式形如&#xff1a; x2y22x2(x2y2)12x^{2}y^{…
阅读更多...
【Qt】Qt 隐式共享

【Qt】Qt 隐式共享

文章目录一、导读二、隐式共享简介三、源码角度分析隐式共享四、隐式共享在开发中的使用五、隐式共享迭代器问题六、隐式共享类和线程一、导读 在实际开发中&#xff0c;Qt中很多类可以直接作为函数参数传递&#xff0c;这样做是为了什么&#xff1f;其背后的实现机制又是什么…
阅读更多...
进程，线程

进程，线程

进程是操作系统分配资源的基本单位&#xff0c;线程是CPU调度的基本单位。 PCB&#xff1a;进程控制块&#xff0c;操作系统描述程序的运行状态&#xff0c;通过结构体task,struct{…}&#xff0c;统称为PCB&#xff08;process control block&#xff09;。是进程管理和控制的…
阅读更多...
#电子电气架构——Vector工具常见问题解决三板斧

#电子电气架构——Vector工具常见问题解决三板斧

我是穿拖鞋的汉子，魔都中一位坚持长期主义的工科男。 今天在与母亲聊天时，得到老家隔壁邻居一位大姐年初去世的消息，挺让自己感到伤感！岁月如流水，想抓都抓不住。想起平时自己加班的那个程度，可能后续也要自己注意身体啦。 老规矩，分享一段喜欢的文字，避免自己成为高知…
阅读更多...
千锋教育嵌入式物联网教程之系统编程篇学习-03

千锋教育嵌入式物联网教程之系统编程篇学习-03

目录 进程的终止 exit函数 _exit函数 进程退出清理 进程间的替换 进程间通信 常见通信机制 进程间通信的实质 信号 产生信号的方式 信号的默认处理方式 进程对信号的处理方式 kill函数 进程的终止 使用exit函数对进程进行终止&#xff0c;而return只是结束函数&a…
阅读更多...
电子技术——共模抑制

电子技术——共模抑制

电子技术——共模抑制 我们在之前学习过&#xff0c;无论是MOS还是BJT的差分输入对&#xff0c;共模信号并不会改变漏极电流的大小&#xff0c;因此我们说差分输入对共模信号无响应。但是实际上由于各种客观非理想因素&#xff0c;例如电流源有限阻抗等&#xff0c;此时共模是影…
阅读更多...
LINUX提权入门手册

LINUX提权入门手册

前言 发点存货 LINUX权限简介 在学习提权之前我们先了解一下linux里面的权限我们使用命令: ls -al即可查看列出文件所属的权限&#xff1a; 文件头前面都有一段类似的字符&#xff0c;下面我们仔细分析一下里面符号分别代表什么。 -rw-r--r-- 1 root root 第一个符号-的…
阅读更多...
现代 cmake (cmake 3.x) 操作大全

现代 cmake (cmake 3.x) 操作大全

cmake 是一个跨平台编译工具&#xff0c;它面向各种平台提供适配的编译系统配置文件&#xff0c;进而调用这些编译系统完成编译工作。cmake 进入3.x 版本&#xff0c;指令大量更新&#xff0c;一些老的指令开始被新的指令集替代&#xff0c;并加入了一些更加高效的指令/参数。本…
阅读更多...
MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程

MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程

目录 数据库简介 MongoDB数据库的安装 MongoDB数据库的启动 MongoDB数据库环境变量的配置 MongoDB图形化管理工具 数据库简介 在使用MongoDB数据库之前&#xff0c;我们应该要知道我们使用它的原因&#xff1a; 在数据库当中&#xff0c;有常见的三高需求&#xff1a; Hi…
阅读更多...
如何手写一个springboot starter？

如何手写一个springboot starter？

本文主要分享了如何手写一个spring starter&#xff0c;把你的代码作为jar包进行开源。命名规则&#xff08;不要使用spring-boot开头&#xff0c;以避免将来spring-boot官方使用你的starter而重名&#xff09;官方命名格式为&#xff1a;spring-boot-starter-xxx非官方命名格式…
阅读更多...
ucos-ii 的任务调度原理和实现

ucos-ii 的任务调度原理和实现

ucosii 任务调度和原理1、ucos-ii 任务创建与任务调度 1.1、任务的创建 当你调用 OSTaskCreate( ) 进行任务的创建的时候&#xff0c;会初始化任务的堆栈、保存cpu的寄存器、创建任务的控制块&#xff08;OS_TCB&#xff09;等的操作&#xff1b; if (OSTCBPrioTbl[prio] (OS_…
阅读更多...
Python中如何书写文件路径

Python中如何书写文件路径

当程序运行时&#xff0c;变量是保存数据的好方法&#xff0c;但变量、序列以及对象中存储的数据是暂时的&#xff0c;程序结束后就会丢失&#xff0c;如果希望程序结束后数据仍然保持&#xff0c;就需要将数据保存到文件中。Python 提供了内置的文件对象&#xff0c;以及对文件…
阅读更多...
数据库 delete 表数据后，磁盘空间为什么还是被一直占用?

数据库 delete 表数据后，磁盘空间为什么还是被一直占用?

插&#xff1a; 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 坚持不懈&#xff0c;越努力越幸运&#xff0c;大家一起学习鸭~~~ 最近有个上位机获取下位机上报数据的项目&#xff0c…
阅读更多...
计算机网络6：Http协议

计算机网络6：Http协议

目录HTTP1.基本概念1.1.1 URI2. 请求和响应报文2.1.请求报文2.2.响应报文3.HTTP报文实现细节3.1响应头主要字段3.2HTTP状态码3.3 HTTP方法3.3.1 GET方法3.3.2 HEAD3.3.3 POST3.3.4 PUT3.3.5 PATCH3.3.6 DELETE3.3.7 OPTIONS3.3.8 CONNECT3.4 HTTP首部&#xff08;头部&#xff…
阅读更多...
【MT7628】开发环境搭建-Fedora12安装之后无法上网问题解决

【MT7628】开发环境搭建-Fedora12安装之后无法上网问题解决

1.按照如下图所示，打开Network Connections 2.点击Network Connections，弹出如下界面
阅读更多...
面向对象程序（C++）设计基础

面向对象程序（C++）设计基础

一、类&对象C 在 C 语言的基础上增加了面向对象编程&#xff0c;C 支持面向对象程序设计。类是 C 的核心特性&#xff0c;通常被称为用户定义的类型。类提供了对象的蓝图&#xff0c;所以基本上&#xff0c;对象是根据类来创建的。声明类的对象&#xff0c;就像声明基本类型…
阅读更多...
面试题(二十二)消息队列与搜索引擎

面试题(二十二)消息队列与搜索引擎

2. 消息队列 2.1 MQ有什么用&#xff1f; 参考答案 消息队列有很多使用场景&#xff0c;比较常见的有3个&#xff1a;解耦、异步、削峰。 解耦&#xff1a;传统的软件开发模式&#xff0c;各个模块之间相互调用&#xff0c;数据共享&#xff0c;每个模块都要时刻关注其他模…
阅读更多...
Grafana 系列文章（十五）：Exemplars

Grafana 系列文章（十五）：Exemplars

Exemplars 简介 Exemplar 是用一个特定的 trace&#xff0c;代表在给定时间间隔内的度量。Metrics 擅长给你一个系统的综合视图&#xff0c;而 traces 给你一个单一请求的细粒度视图&#xff1b;Exemplar 是连接这两者的一种方式。 假设你的公司网站正经历着流量的激增。虽然…
阅读更多...
ansible的模块详解

ansible的模块详解

ansible 的概述 什么是ansible Ansible是一款为类Unix系统开发的自由开源的配置和自动化工具。 它用Python写成&#xff0c;类似于saltstack和Puppet&#xff0c;但是有一个不同和优点是我们不需要在节点中安装任何客户端。 它使用SSH来和节点进行通信。Ansible基于 Python…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023