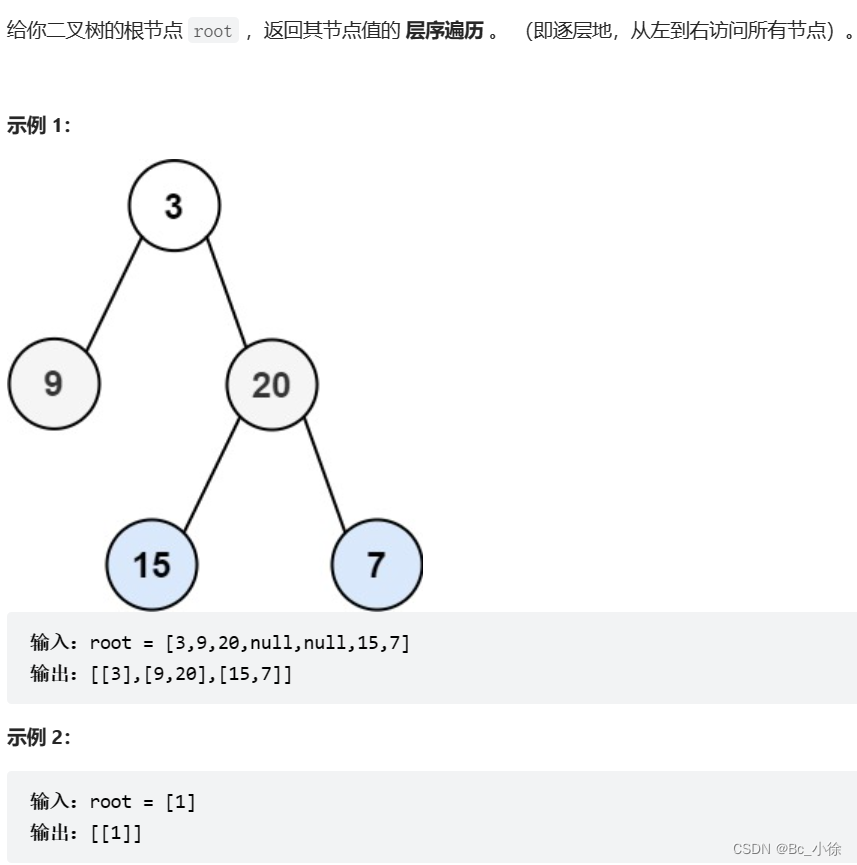
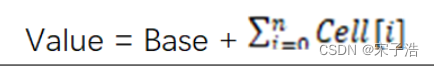文章目录
- Step 1: Function Set
- Step 2: Goodness of a Function
- Step 3: Find the best function
- Why not Logistic Regression + Square Error
- Discriminative v.s. Generative
- Multi-class Classification(3 Class)
- Limitation of Logistic Regression
- Cascading logistic regression models
- Deep Learning!
上次通过贝叶斯推导出了一个线性的函数，这里尝试直接求解这个函数并称其为逻辑回归
Step 1: Function Set
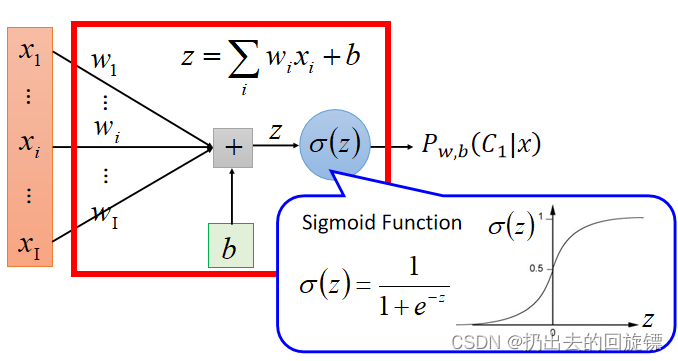
它与linear regression模型不同在于输出：
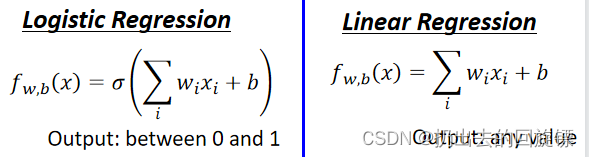
其中
w
:
w
i
g
h
t
w:wight
w:wight ,
b
:
b
i
a
s
b:bias
b:bias ,
x
i
:
i
n
p
u
t
x_i:input
xi:input
Step 2: Goodness of a Function
假设N个training data从函数
f
w
,
b
(
x
)
=
P
w
,
b
(
C
1
∣
x
)
f_{w,b}(x)=P_{w,b}(C_1|x)
fw,b(x)=Pw,b(C1∣x)产生，现在需要找到最好的参数
w
∗
w^*
w∗和
b
∗
b^*
b∗使
L
(
w
,
b
)
L(w,b)
L(w,b)（likelihood）最大，公式表达如下：
通过对数似然可以转化成求解最小值，相乘转化成相加，同时约项有：
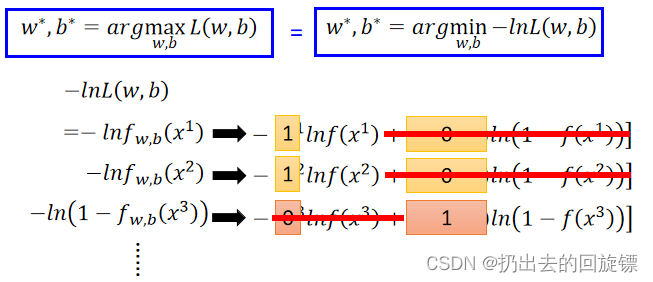
合并累加有：
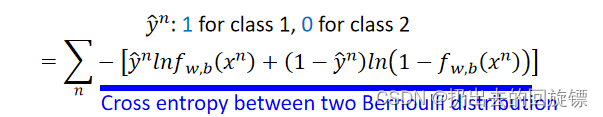
Cross entropy意思是交叉熵，可以理解为两个伯努利分布的损失函数，当两者一样结果为0。与Linear Regression对比如下：
Step 3: Find the best function
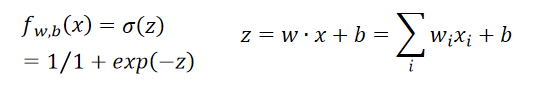
原始求解函式如下：
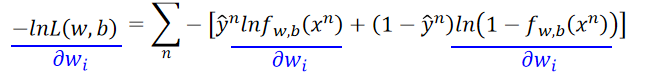
第一项计算得：
第二项计算得：
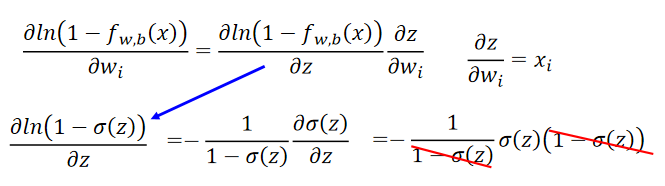
代入原式整理后有：
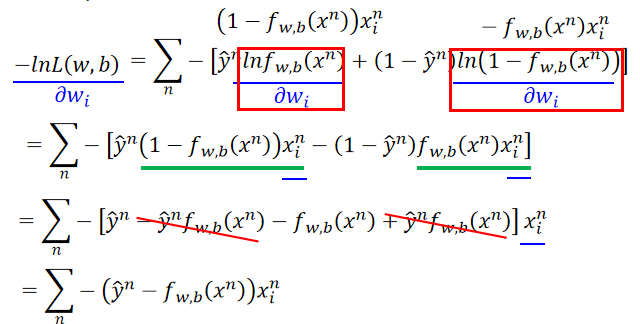
由这个结果可以知道，权重更新由3个参数决定：learning rate，x,
y
^
n
−
f
w
,
b
(
x
n
)
\hat y_n-f_{w,b}(x^n)
y^n−fw,b(xn)即预测与实际的差异，表示如下：
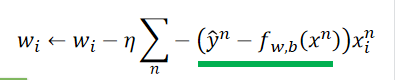
Linear Regression与Logistic Regression梯度下降更新步骤相同：
但要注意Logistic的
y
^
\hat y
y^是0或1，而Linear的是任意实数
Why not Logistic Regression + Square Error
三步建立Model如下：
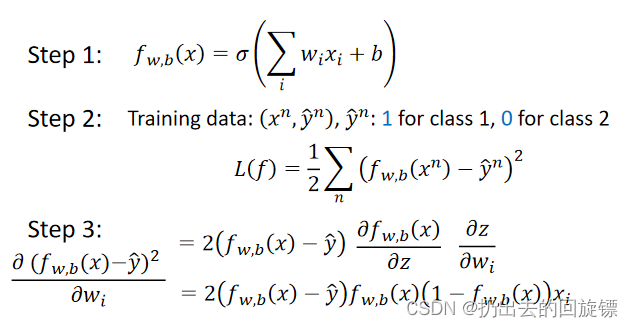
但是这样会出现混淆，样本距离目标很近或很远时梯度计算都很小，这样会导致距离远时收敛过慢
对比图如下：
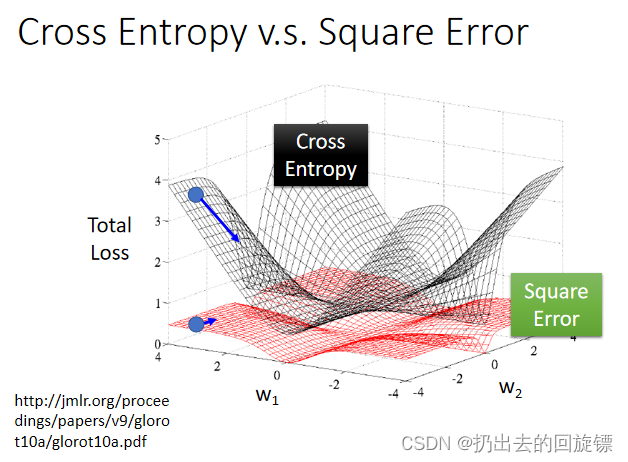
可以看到，Cross Entropy距离目标越远，微分值越大，参数update越快；Square Error距离目标很远时候，微分值很小，参数update就很慢。可能你会想到，我们可以在Square Error的微分值很小的时候把learning rate设的大一点，但微分值很小的时候，也有可能是距离目标值很近，我们分不清楚微分值小时候是距离目标很近还是很远，所以没办法确定learning rate设置是小还是大。所以， 我们使用Cross Entropy可以让training顺利很多。
Discriminative v.s. Generative
- 判别模型：如logistic regression直接寻找w和b
- 生成模型：如Gaussian先假设再寻找（脑补特性）
不同方式具体表示图如下：
在本次实验中两者表现如下：
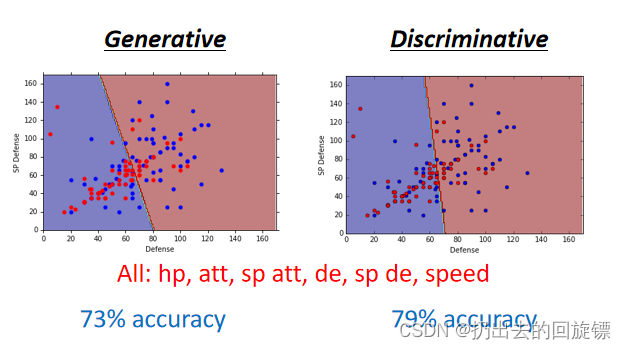
可以看到判别式效果好一些，一般也认为判别式效果更加。生成式有优势具体场景如下：
| Generative | Discriminative | |
|---|---|---|
| 概率 | 联合概率P(X,Y) | 后验概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) |
| 解释 | 首先建立样本的联合概率概率密度模型P(X,Y)，然后再得到后验概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)，再利用它进行分类(所有概率进行比较，取最大的一个） | 输入属性X可以直接得到Y。有限样本条件下建立判别函数，不考虑样本的产生模型，直接研究预测模型 |
| 特点 | 尝试去找到底数据是怎么生成的，基于假设 | 不进行过多假设，不关心数据产生，只关心差异 |
| 优点 | 生成模型收敛速度比较快，即当样本数量较多时，生成模型能更快地收敛于真实模型 | 直接学习 P ( Y ∣ X ) P(Y|X) P(Y∣X)或f(X)，可以对数据进行抽象、定义特征并使用特征，因此可以简化学习问题。直接面对预测，准确率较高 |
| 缺点 | 需要更多的样本和更多计算，只需要做分类任务，就浪费了计算资源 | 决策函数Y=f(X)或者条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)，不能反映训练数据本身的特性 |
Multi-class Classification(3 Class)
计算不同类别的z值，放入Softmax函数中（又称激活函数，即取指数后归一）
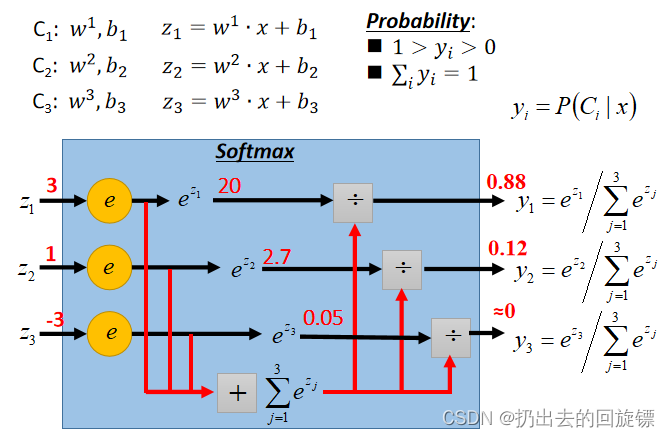Softmax拉大最大值与最小值的差距，即强化最大值。之后就可以计算预测和真实的交叉熵
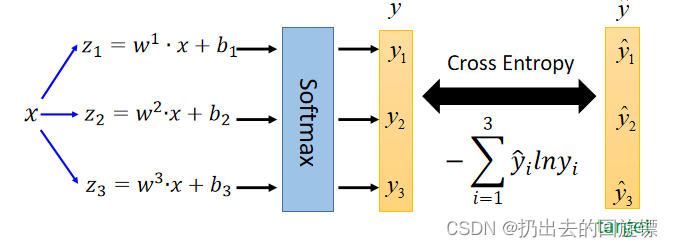
需要注意给分类增加限制，采用one-hot编码
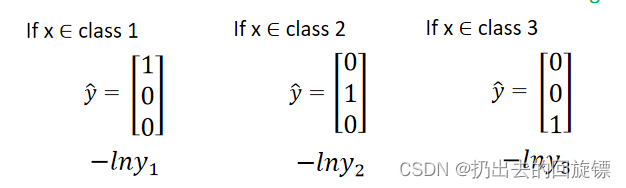
Limitation of Logistic Regression
某些时候，Logistic Regression并不能做到分类成功，但数据有一个异或的关系时，是无论无和都分类不成功的：
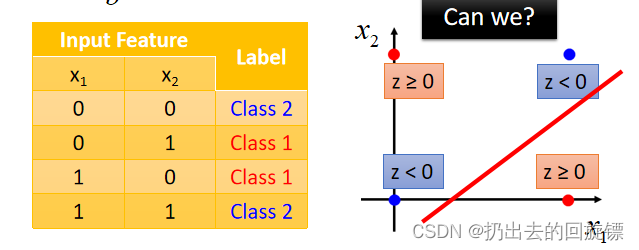
可以人为Feature Transformation将样本位置进行转换尝试分类：
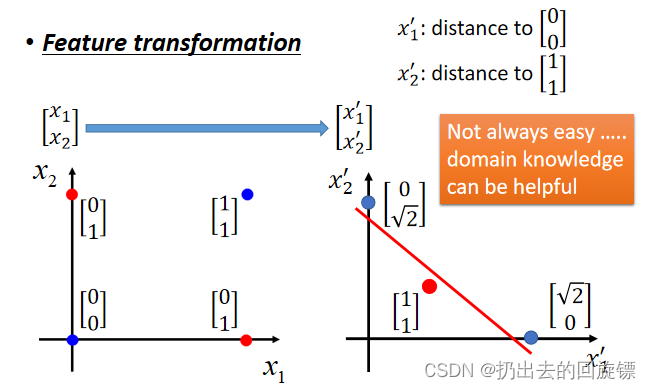
需要一种机器帮助Transformation的算法，下面就是咯！
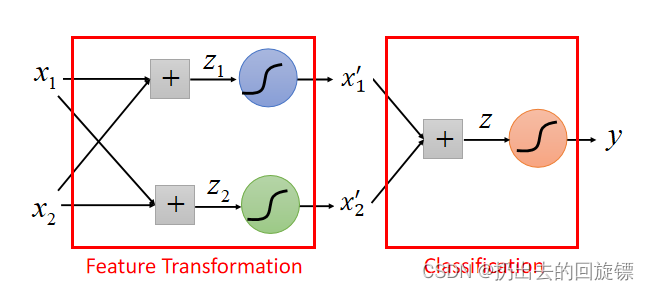
Cascading logistic regression models
将样本的Logistic 用来做feature transformation，再另外用一个Logistic预测，具体图如下：
效果图如下：
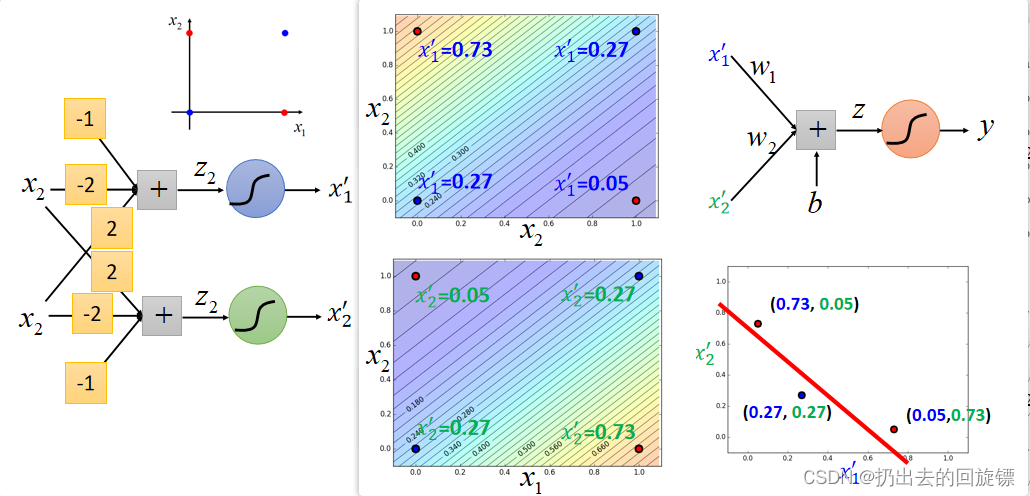
Deep Learning!
多层的特征转换就形成了Neural Network（神经网络）即Deep learning 的领域！
