sklearn降维算法1 - 降维思想与PCA实现

1、概述

1.1 维度概念

shape返回的结果，几维几个方括号嵌套
在这里插入图片描述
特征矩阵特指二维的
一般来说，维度指的是样本的数量或特征的数量
降维算法，指降低特征矩阵中特征的数量。降维是为了让算法运算能更快，效果更好，但还有一种需求：数据可视化（三维以上的无法可视化）

sklearn中降维算法被包括在模块decomposition中，这是一个矩阵分解模块
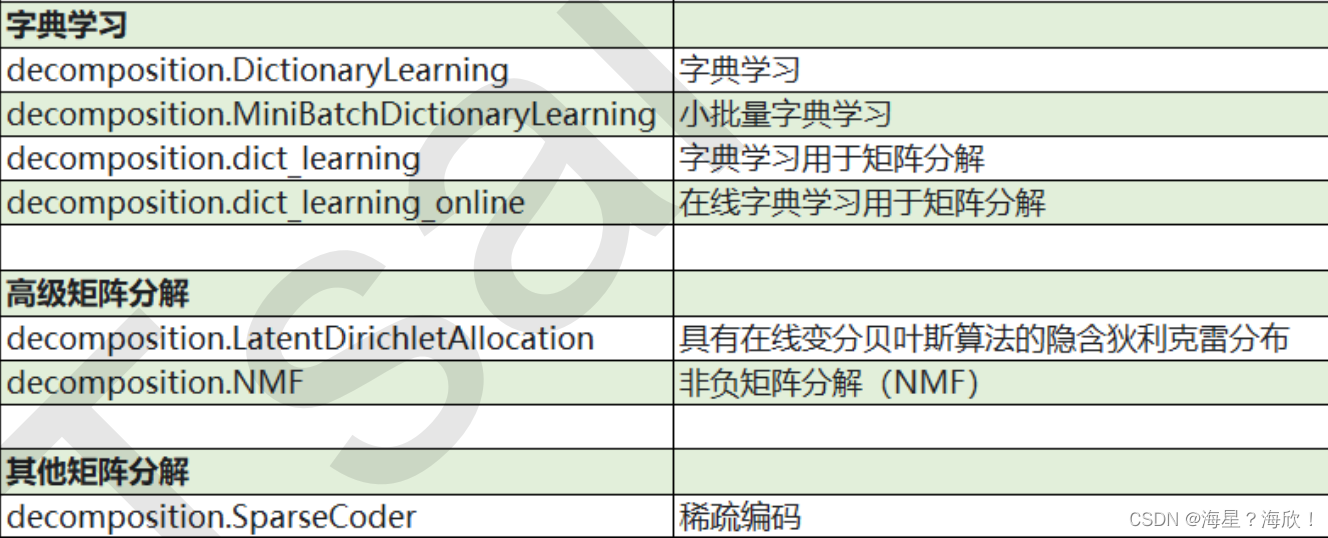
在这里插入图片描述

SVD和主成分分析PCA属于矩阵分解算法中的入门算法，都是通过分解特征矩阵来降维。

2、PCA与SVD

特征选择方法：方差过滤。
如果一个特征的方差很小，则意味着这个特征上很可能有大量取值都相同（比如90%都是1，只有10%是0，甚至100%是1），那这一个特征的取值对样本而言就没有区分度，这种特征就不带有有效信息。从方差的这种应用就可以推断出，如果一个特征的方差很大，则说明这个特征上带有大量的信息。
因此，在降维中，PCA使用的信息量衡量指标，就是样本方差，又称可解释性方差，方差越大，特征所带的信息量越多。

在这里插入图片描述
问：方差计算公式中为什么除数是n-1?
答：这是为了得到样本方差的无偏估计

2.1 降维实现

sklearn.decomposition.PCA

举一个栗子：
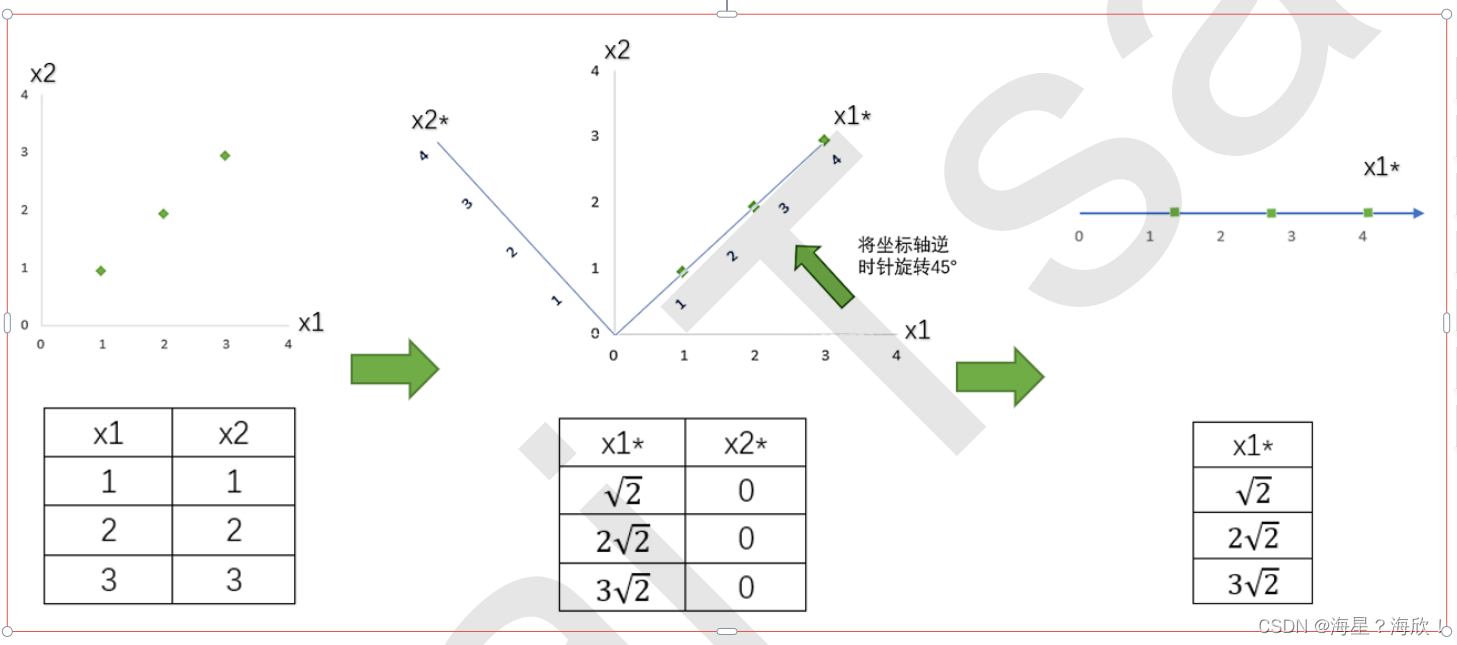
原数据，特征x1和x2，三个样本点，在二维平面中可以作图出来，现在每个数据特征的均值是2，方差计算出来为1

目标：进行降维，只用一个一个特征向量来描述这组数据，即将二维数据降为一维数据，并且尽可能地保留信息量，即让数据的总方差尽量靠近2。于是，我们将原本的直角坐标系逆时针旋转45°，形成了新的特征向量x1和x2组

新数据：x2上的数值此时都变成了0，因此x2明显不带有任何有效信息了（此时x2的方差也为0了）。此时，x1特征上方差为2

结果：根据信息含量的排序，取信息含量最大的一个特征，因为我们想要的是一维数据。所以我们可以将x2删除，同时也删除图中的x2特征向量，剩下的x1*就代表了曾经需要两个特征来代表的三个样本点。
通过旋转原有特征向量组成的坐标轴来找到新特征向量和新坐标平面，我们将三个样本点的信息压缩到了一条直线上，实现了二维变一维，并且尽量保留原始数据的信息。一个成功的降维，就实现了。
在这里插入图片描述
将二维特征矩阵进行推广：
二维特征矩阵：

输入原数据，结构为 (3,2) 找出原本的2个特征对应的直角坐标系，本质是找出这2个特征构成的2维平面
决定降维后的特征数量：1
旋转，找出一个新坐标系。新特征向量让数据能够被压缩到少数特征上，并且总信息量不损失太多
找出数据点在新坐标系上，2个新坐标轴上的坐标
选取第1个方差最大的特征向量，删掉没有被选中的特征，成功将2维平面降为1维

n维特征矩阵：

输入原数据，结构为 (m,n) 找出原本的n个特征向量构成的n维空间V
决定降维后的特征数量：k
通过某种变化，找出n个新的特征向量，以及它们构成的新n维空间V
找出原始数据在新特征空间V中的n个新特征向量上对应的值，即“将数据映射到新空间中”
选取前k个信息量最大的特征，删掉没有被选中的特征，成功将n维空间V降为k维

五步骤：原数据特征 - 降维数 - 变换成新特征空间 - 数据映射到新空间 - 按信息量排序，取前k个

步骤3中，变化找到新特征向量，让数据能够被压缩到少数特征上并且总信息量不损失太多的技术就是矩阵分解。

PCA和SVD比较
PCA和SVD是两种不同的降维算法，但他们都遵从上面的过程来实现降维，只是两种算法中矩阵分解的方法不同，信息量的衡量指标不同罢了。

PCA使用方差作为信息量的衡量指标，并且特征值分解来找出空间V。降维完成之后，PCA找到的每个新特征向量就叫做“主成分”，而被丢弃的特征向量被认为信息量很少，这些信息很可能就是噪音。

而SVD使用奇异值分解来找出空间V，其中Σ也是一个对角矩阵，不过它对角线上的元素是奇异值

问题：
无论是PCA和SVD都需要遍历所有的特征和样本来计算信息量指标。并且在矩阵分解的过程之中，会产生比原来的特征矩阵更大的矩阵
无论是Python还是R，或者其他的任何语言，在大型矩阵运算上都不是特别擅长，无论代码如何简化，我们不可避免地要等待计算机去完成这个非常庞大的数学计算过程。因此，降维算法的计算量很大，运行比较缓慢，但无论如何，它们的功能无可替代

PCA和特征选择都是特征工程的一部分，两者区别？

答：特征工程中有三种方式：特征提取，特征创造和特征选择。
特征选择是从已存在的特征中选取携带信息最多的，选完之后的特征依然具有可解释性，我们依然知道这个特征在原数据的哪个位置，代表着原数据上的什么含义。
而PCA，是将已存在的特征进行压缩，降维完毕后的特征不是原本的特征矩阵中的任何一个特征，而是通过某些方式组合起来的新特征。通常来说，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向量，新特征矩阵生成之后也不具有可读性，我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而来，新特征虽然带有原始数据的信息，却已经不是原数据上代表着的含义了。以PCA为代表的降维算法因此是特征创造的一种。
PCA一般不适用于探索特征和标签之间的关系的模型（如线性回归），因为无法解释的新特征和标签之间的关系不具有意义。在线性回归模型中，我们使用特征选择。

2.2 重要参数n_components

n_components是我们降维后需要的维度，即降维后需要保留的特征数量K，
[0, min(X.shape)]范围中的整数

问题：
如果留下的特征太多，就达不到降维的效果，如果留下的特征太少，那新特征向量可能无法容纳原始数据集中的大部分信息，因此，n_components既不能太大也不能太小
解决：如果降维目标是可视化，希望可视化一组数据来观察数据分布，我们往往将数据降到三维以下，很多时候是二维，即n_components的取值为2。

2.2.1 案例：高维数据的可视化

可视化：至少要降维到3维
1，导模块

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris #鸢尾花数据
from sklearn.decomposition import PCA

2，数据了解

iris = load_iris()
y = iris.target
x = iris.data
x.shape  #(150,4)-150条样本，4个特征，4维度

import pandas as pd
pd.DataFrame(x)

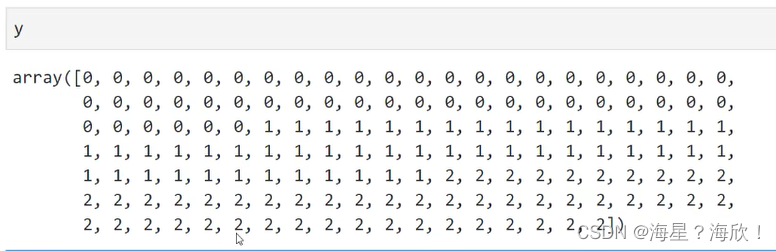
在这里插入图片描述
y的输出,三种可能
3，降维：

#调用PCA
pca = PCA(n_components=2) #实例化
pca = pca.fit(x) #拟合模型
x_dr = pca.transform(x) #获取新矩阵
x_dr.shape  #输出（150，2）降维到了2维

#fit_transform一步到位
#x_dr = PCA(2).fit_transform(x)

4，可视化
对于得到的x_dr
在这里插入图片描述

x_dr[y==0,0]#取出标签为0的记录的，第一列的数据

在这里插入图片描述

plt.figure() #要画图，给一个画布
plt.scatter(x_dr[y==0,0],x_dr[y==0,1],c=c="red", label=iris.target_names[0]) #标签为0的数据，散点图x提供横纵坐标，y表现不同颜色
#iris.target_names特征名字
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()

在这里插入图片描述
上面的作图代码，可以用for循环实现一下：
对数据，名字，颜色都循环

colors = ['red','black', 'orange']

plt.figure()
foriin [0, 1, 2]:
    plt.scatter(X_dr[y == i, 0]
                ,X_dr[y == i, 1]
                ,alpha=.7  #颜色透明度
                ,c=colors[i]
                ,label=iris.target_names[i]               )
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()

鸢尾花数据集，是一个明显的分簇分布。一个有很好效果的数据集

5，探索降维后数据：
explained_variance_，查看降维后每个新特征向量上所带的信息量大小

#属性explained_variance_，查看降维后每个新特征向量上所带的信息量大小（可解释性方差的大小）pca.explained_variance_

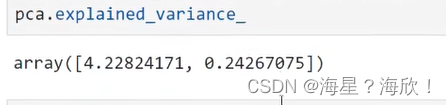
在这里插入图片描述
降维后剩下的x1和x2，所以返回了这两个的方差

explained_variance_ratio，查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比

#属性explained_variance_ratio，查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比#又叫做可解释方差贡献率
pca.explained_variance_ratio_
#大部分信息都被有效地集中在了第一个特征上

在这里插入图片描述
结果显示，原始总信息的92%在新特征x1上，原始总信息的5%在新特征x2上

pca.explained_variance_ratio_.sum()

输出97.76%，说明原始信息的97%都留在了新特征上。特征减掉了两个，而信息损失不到3%。–PCA效果好

6，选择最好的n_components：累积可解释方差贡献率曲线

累积可解释方差贡献率曲线是一条以降维后保留的特征个数为横坐标，降维后新特征矩阵捕捉到的可解释方差贡献率为纵坐标的曲线，能够帮助我们决定n_components最好的取值。

当参数n_components中不填写任何值，则默认返回min(X.shape)个特征，可以画出累计可解释方差贡献率曲线

pca_line = PCA().fit(X)
pca_line.explained_variance_ratio_

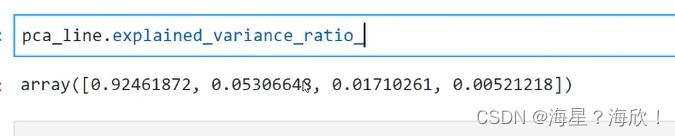
在这里插入图片描述
返回的是，每个特征带有的原始信息的占比

import numpy as np
np.cumsum(pca_line.explained_variance_ratio_) #返回的是累加

import numpy as np
pca_line = PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
#上面的[1,2,3,4]是x的取值，不写，会自动写入坐标
plt.xticks([1,2,3,4]) #这是为了限制坐标轴显示为整数
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

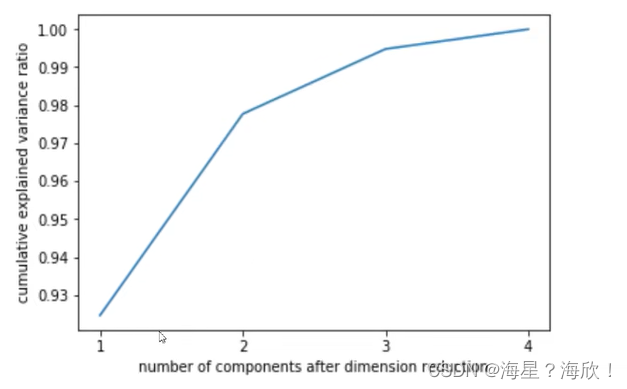
在这里插入图片描述
找图像中的转折点

2.2.2 最大似然估计自选超参数

除了输入整数，n_components还有哪些选择呢？
PCA可以用最大似然估计(maximum likelihood estimation)自选超参数的方法，输入“mle”作为n_components的参数输入，就可以调用这种方法。

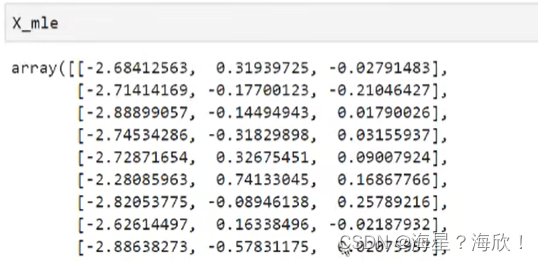
pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)

X_mle #自动选择了三列特征

在这里插入图片描述

pca_mle.explained_variance_ratio_.sum()
#0.994
#得到了比设定2个特征时更高的信息含量，对于鸢尾花这个很小的数据集来说，3个特征对应这么高的信息含量，并不需要去纠结于只保留2个特征，毕竟三个特征也可以可视化

2.2.3 按信息量占比选超参数

输入[0,1]之间的浮点数，并且让参数svd_solver ==‘full’，表示希望降维后的总解释性方差占比大于n_components 指定的百分比，即是说，希望保留百分之多少的信息量。

比如说，如果我们希望保留97%的信息量，就可以输入
n_components = 0.97，PCA会自动选出能够让保留的信息量超过97%的特征数量。

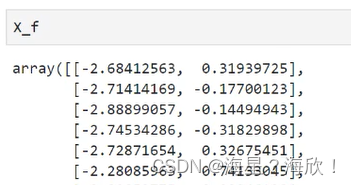
pca_f = PCA(n_components=0.97,svd_solver="full") #帮忙选出总信息占比超过97%的特征
pca_f = pca_f.fit(X)
X_f = pca_f.transform(X)
X_f #自动选择了两维

在这里插入图片描述

pca_f.explained_variance_ratio_  #[0.92,0.053]

pca_f.explained_variance_ratio_.sum() #0.97