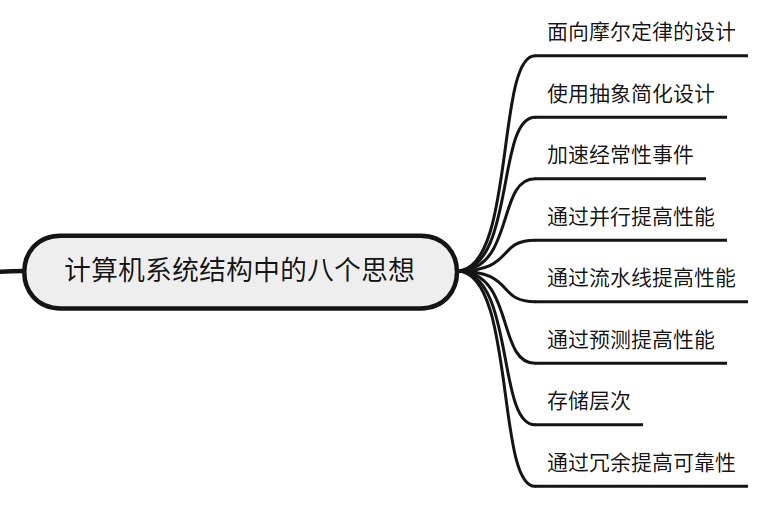
计算机体系结构中的 8 个伟大思想

面向摩尔定律的设计

摩尔定律指出单芯片上所集成的晶体管资源每 18 至 24 个月翻一倍。
由于计算机设计需要花费很长时间，因此项目结束时，每个芯片的可用晶体管资源相对设计开始时可以轻易实现双倍或四倍增长。
计算机架构师必须预测其设计完成时的工艺水平，而不是设计开始时的工艺水平。

使用抽象简化设计

提高硬件和软件生产率的主要技术之一是使用抽象来表示不同的设计层次 —— 隐藏低层细节以提供给高层一个更简单的模型。

相关例子：

• 通过高级语言所编写的应用软件最终需要通过编译器转换为计算机可以识别的机器指令，因为上一级隐藏了低一级的细节。

加速经常性事件

加速经常性事件远比优化罕见情形能够更好地提升性能。
我的理解是：对代码已知可能发生的一些场景进行一些优化处理，而这些场景就是所谓的“经常性事件”，这些场景只有通过仔细的实验和测量才能得出，罕见的情形就不是不经常出现的情况，因此相比之下就显得不那么重要了。

通过并行提高性能

并行计算可以获得更高的性能。

通过流水线提高性能

并行性的一种特殊场景在计算机体系结构中非常普遍，因此它有着专门的名称：流水线。

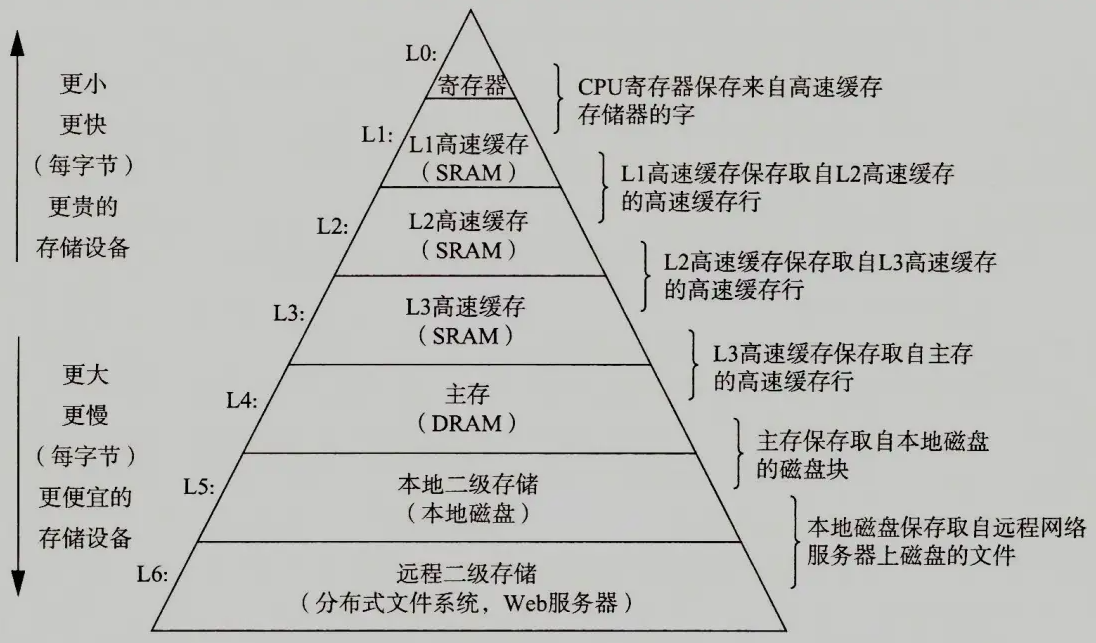
存储层次

通过冗余提高可靠性

由于物理设备可能发生故障，因此可通过引入冗余的组件使系统更可靠，该组件在系统发生故障时可代替失效组件并帮助检测故障。

引入的组件其实就是物理设备的副本，也就是有多个相同的物理设备，若某个设备坏了，这些备用设备可顶替上去。

性能

性能的度量

时间是计算机性能的衡量标准：完成同样的计算任务，用时最短的计算机是最快的。

程序的执行时间一般以秒为单位。响应时间、挂钟时间、运行时间等这些属于均表示某项任务所需的总时间，包括硬盘访问、内存访问、IO活动和操作系统开销等一系列时间。

计算机经常被共享使用，一个处理器可能同时运行多个程序。在这种情况下，系统可能更侧重于优化吞吐率，而不是致力于将单个程序的执行时间变得更短。

疑惑：把程序执行时间缩短了，不就更快了吗？为什么却侧重于优化吞吐率呢？
答：程序的可变因素有很多，例如内存访问、磁盘访问、IO操作等，你可能在执行某部分程序类型的时候快一些，但换到另一种类型的程序时就效果没那么显著了，所以不妨从整体上去优化吞吐率。

因此我们需要把运行任务本身的时间与其它时间区分开。

这里使用 CPU 执行时间来区分，简称 CPU 时间，只表示在 CPU 上所花费的时间，而不包括等待 IO 或运行其它程序的时间。

Tips：用户所感受到的是程序的运行时间，而不是 CPU 时间。

CPU 时间还可继续细分为：

• 用户 CPU 时间： 执行用户程序本身所花费的时间。
• 系统 CPU 时间： 为用户程序执行相关任务所花费的时间。

很难做到精确的区分这两种 CPU 时间，因为通常难以分清哪些操作系统的活动是属于哪个用户进程的，而且不同操作系统的功能也千差万别。

采用 CPU 性能表示用户 CPU 时间。

计算机硬件完成基本功能的速度的度量单位是时钟周期数，也称滴答数、时钟滴答数、时钟数、周期数。

• 时钟周期数：计算机一个时钟周期的时间，通常是指处理器时钟，并在固定频率下运行。
• 时钟周期的表示方式：
  • 完整时钟周期的时间：例如 250皮秒或 250ps。
  • 时钟周期的倒数，即时钟频率，即 1/时钟周期数，例如 4GHz。
• 周期长度：每个时钟周期持续的时间长度。

时钟周期数和时钟周期长度与CPU时间的公式

$$程序的CPU执行时间=程序的CPU时钟周期数\times 时钟周期长度$$

由于时钟频率和时钟周期长度互为倒数，故另一种表达形式为：

$$程序的CPU执行时间=\frac{程序的CPU时钟周期数}{时钟频率}$$

指令性能公式

$$CPU时钟周期数=程序的指令数\times 指令平均时钟周期数$$

指令平均时钟周期数（CPI）： 表示执行每条指令所需的时钟周期平均数。

经典的 CPU 性能公式

$$CPU时间=指令数\times CPI\times 时钟周期长度$$

或考虑到时钟频率和时钟周期长度互为倒数，可写为：
$$CPU时间=\frac{指令数\times CPI}{时钟频率}$$
指令数： 执行某程序所需要的总指令数量。

CPI 计算公式

$$CPI=\frac{CPU时钟周期数}{指令数}$$

CPI 对于不同应用程序是不同的，对于相同指令系统的不同实现方式也是不同的。

程序执行时间计算公式

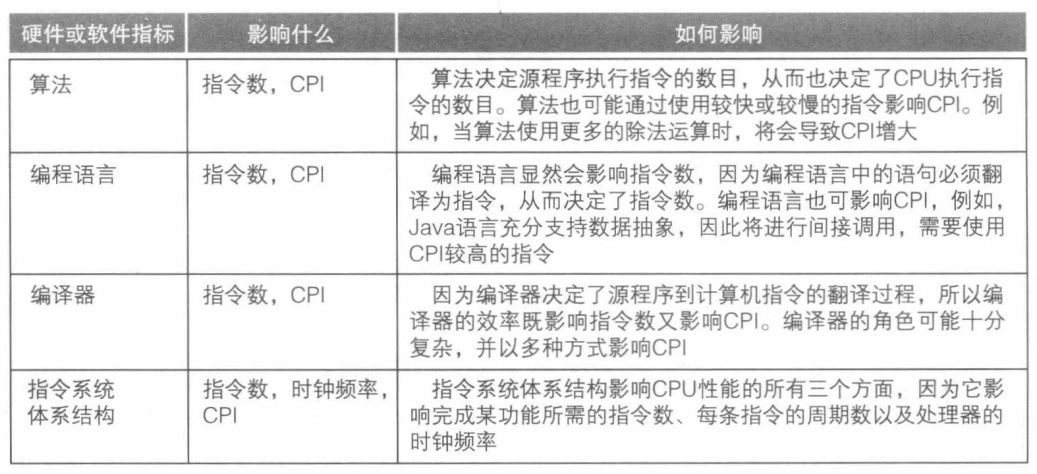
根据图 1-15 所列出的指标，可以计算出程序的执行时间（单位：秒）。
$$执行时间=\frac{秒}{程序}=\frac{指令数}{程序}\times \frac{时钟周期数}{指令}\times \frac{秒}{时钟周期}$$

只用一种因素去评价性能是危险的。当比较两台计算机时必须考虑全部的三个因素，它们组合起来才能确定执行时间。

理解程序性能

程序的性能与算法、编程语言、编译器、体系结构以及实际的硬件有关，如下：

Amdahl 定律

例题：假设一个程序在一台计算机上运行需要 100 秒，其中 80 秒的时间用于乘法操作。如果要把该程序的运行速度提高 5 倍，乘法操作的速度应该要改进多少？
$$改进后的执行时间=\frac{受改进影响的执行时间}{改进量}+不受影响的执行时间$$
本题计算：
$$20=\frac{80}{n}+(100-80)$$
最后得到 $0=\frac{80}{n}$ ，也就是说乘法运算占总负载的 80%，则无论怎样改进乘法，也无法达到性能提高 5 倍的结果。针对特定情况的性能提升，受到被改进的特征所占比例的限制。这个概念在日常生活中被称为收益递减定律。

当我们知道一些功能所消耗的时间及其可能的加速比时，就可以使用 Amdahl 定律对性能提升进行预估。

MIPS 计算公式

$$MIPS=\frac{指令数}{执行时间\times 10^6}$$

MIPS：每秒百万条指令数。

MIPS 是指令执行的速率，它规定了性能与执行时间成反比，越快的计算机具有越高的 MIPS 值。

在同一台计算机上，不同的程序会有不同的 MIPS，因而一台计算机不能拥有单一的 MIPS 分值。例如，将执行时间用 MIPS、CPI、时钟频率代入之后可得：
$$MIPS=\frac{指令数}{\frac{指令数\times CPI}{时钟频率}\times 10^6}=\frac{时钟频率}{CPI\times 10^6}$$

如果一个新程序执行的指令数更多，但每条的执行速度更快，则 MIPS 可能独立于性能而发生变化。

资料

• ABI

• 指令集体系结构

• 动态随机存取存储器

• 静态随机存取存储器

• 只读存储器

• 随机存取存储器

• 快闪存储器

• 辅存