1dB压缩点与三阶交调点

要知道放大器是一个非线性系统，传输函数基本用泰勒级数表示

如果输入信号幅度很小，那么上式中2次及以上的项就可以忽略而成为小信号的情况。在许多情况下我们可以忽略3次以上的项。

如果输入一个正弦信号

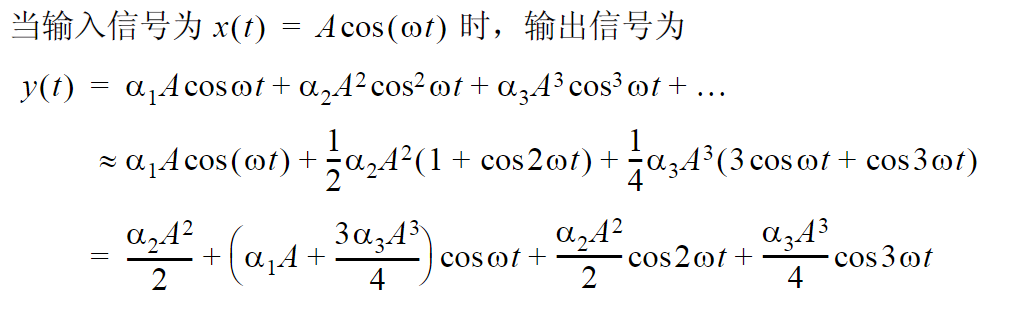
1、可以看到一个单频率信号输入到非线性系统里面就会产生谐波。

2、除了有直流，线性基频，还有一些基频多次方的项，不同谐波频率的项。

如果a1和a3的符号相反，则信号增益将随幅度A的增大而减小。（这种假设并不在所有情况下成立，例如一个共发射极的三极管放大器，其集电极电流与基极电压之间的指数关系使a1和a3的符号相同。这时我们仍然可以观察到增益压缩的情况，这主要是由于晶体管受电源电压的限制工作在非放大区引起的。对于差分电路，包括Bipolar和CMOS，a1和 a3确实具有不同的符号。）

如果用对数(功率)来表示放大器的输入和输出信号幅度，可以清楚地看到输出功率随输
入功率增大而偏离线性关系的情况。

当输出功率与理想的线性情况偏离达到1dB时，放大器的增益也下降了1dB，此时的输入信号功率(或幅度)值称为1-dB增益压缩点(1-dB Gain Compression Point)

如果输入两个正弦信号

相当于信号加一个干扰。会产生谐波和互调分量。

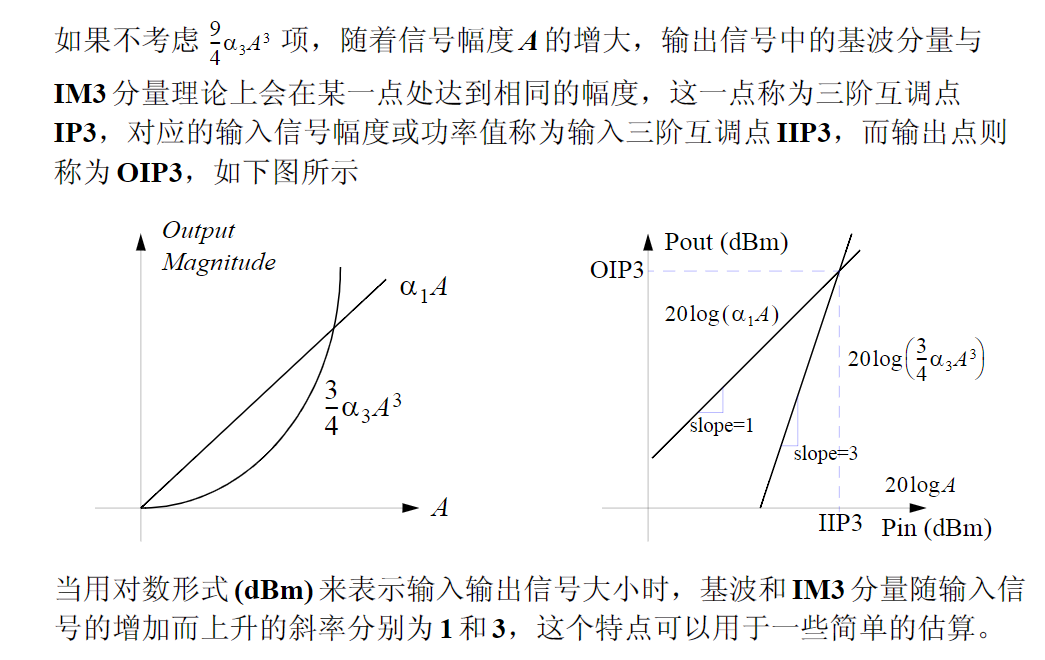
三阶交调点和1dB压缩点的关系，可以知道，三阶交调点相对于1dB压缩点是固定的，1dB压缩点相同，三阶交调点也相同。而1dB压缩点，是由器件本身非线性系数决定，也就是器件本身属性。

从实际数据手册看看是不是对的

HMC504和HMC751，输出三阶交调点接近，分别25.5和25。1dB压缩点应该小10dB左右，15dBm左右。

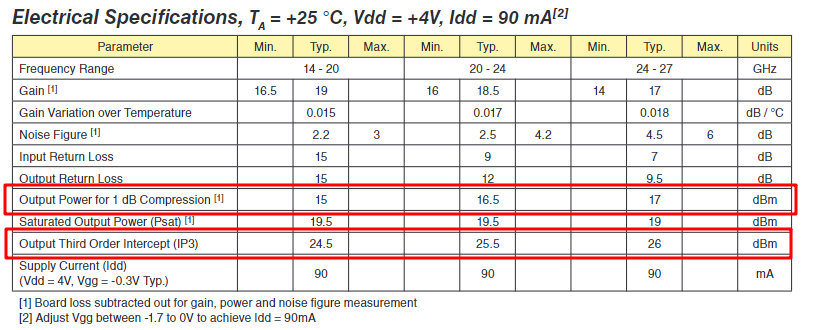
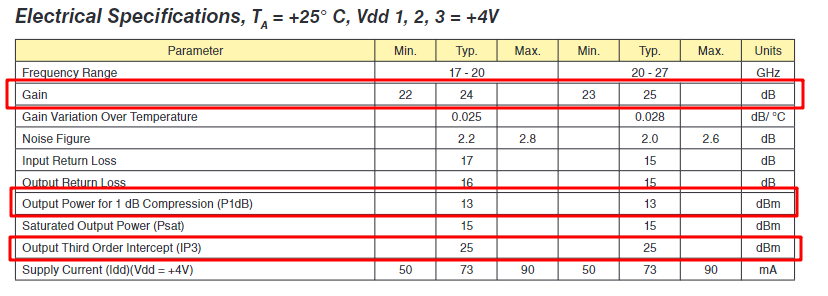
1dB压缩点

这个指标用在放大器上，低噪放和功放都有，通常是OP1dB，输出1dB压缩点。

一个放大器，增益一定，输入多少放大多少倍。但是我一直提高输入，输入多大都可以吗。它都能放大相同的倍数？

1dB压缩点就是用来衡量，它最多能放大多大的信号，输入最大多少。

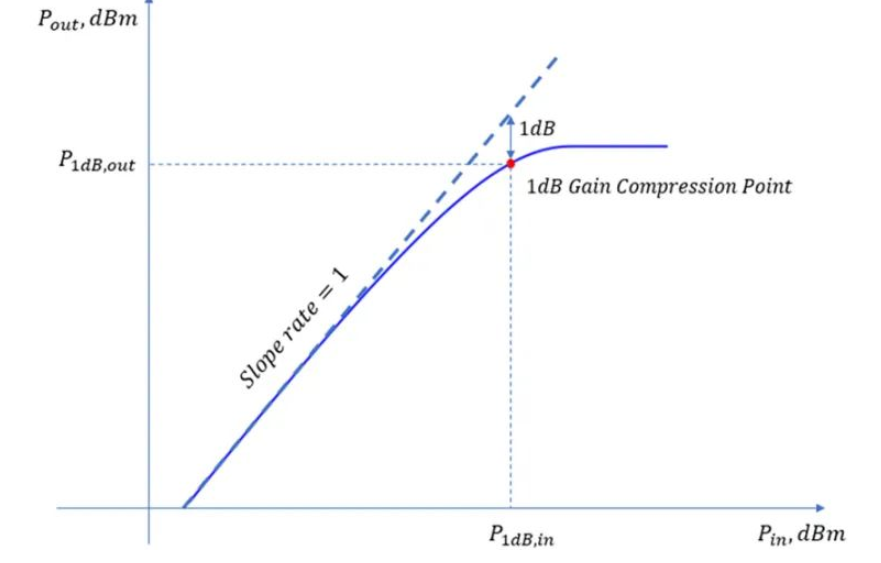
如下面这个图。一个正常的放大器，输入与输出的关系，是下面的曲线。都是用对数表示，dBm。

y=ax，a=y/x，y是输出功率，x是输入功率，a就是增益，也是斜率。

对数形式：Pout(dBm)=Pin (dBm)+G(dB)

可以看到，随着输入功率的增大，输出功率增大得速度变慢，越来越偏离理想的曲线，增益逐步变低，这就是增益压缩效应。

斜率变小，说明增益较小，输出实际减小了，能量肯定跑到其它地方去了。也就是出现非线性效应，信号频率的功率在减小，出现谐波，也就是噪声，它们的功率在快速增大。从而对邻带或带内造成干扰。

实际增益比线性增益跌落1dB的位置，称之为1dB增益压缩点，该点对应的输入、输出功率一般分别标记为P1dB,in 和P1dB,out,OP1dB 。

所以放大器应该工作在1dB压缩点以内。放大区工作在线性区，不会参数谐波分量。

测试：
https://www.cnblogs.com/txqtxg/p/15976492.html

三阶交调点，IP3

三阶交调点，三阶截取点（IP3），一般用输出三阶交调点（OIP3）：主要是表达放大器失真性能的参数。

三阶交调是什么意思呢？

放大器的输入存在两个相近频率的信号。有下面两种情况
1、或者存在相近频率的干扰
2、放大器工作在非线性区，也就是1dB以上或者附近。也会产生谐波。

两个相近频率的信号又会相互影响产生不同频率的信号。如下图所示

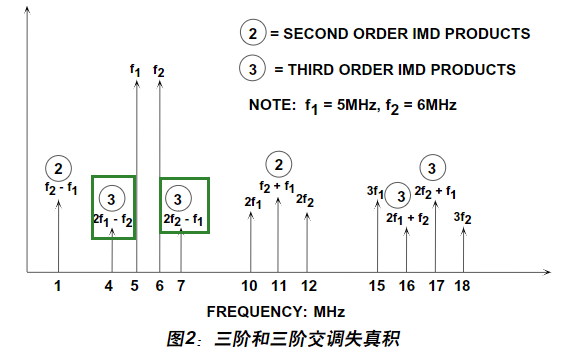
为什么要用三阶交调点呢？

图中即为三阶交调，之所以单独考虑三阶交调，是因为三阶交调距离真实信号非常近，难以通过滤波的方式去除，因此对信号的影响最大。而且三阶交调分量的功率电平最大。

IP3越高表示线性度越好和更少的失真。

三阶截点越高，表征系统线性度越好。

怎么测量得到三阶交调点？

输入两个基频双音信号，即使放大器工作在线性放大区，也会产生三阶交调现象，只要做出输入和输出关系曲线，找到三阶信号和基频信号的1dB压缩点即可，再延长斜率曲线，交点即三阶交调点。

三阶交调信号的增益时基频信号的增益不一样，它们必相交。如下图

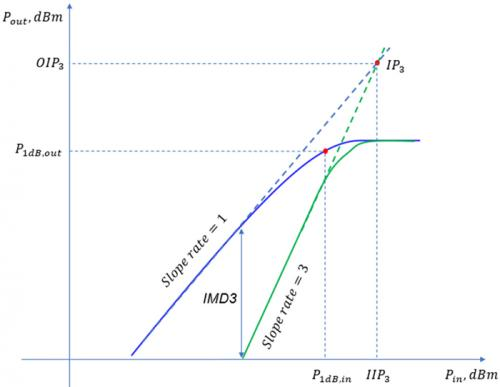
当输入信号足够小放大器工作在线性区，交调失真不会恶化，保持在一个比较均衡的水平；随着输入到DUT的功率的增大，放大器逐渐进入压缩区，交调失真将发生快速恶化。

OIPdBm = GdBm + IIPdBm

参考
https://rf.eefocus.com/article/id-335037

相位差与延迟

同轴电缆中电压信号相位差与延迟的关系

相位差，顾名思义，就是两个波之间相位差的值。

为简化概念，特指正弦波，假设有两个电压信号

$\begin{array}{l}{\mathrm{u}}_1(\mathrm{t})={\mathrm{A}}_1\sin \left({\theta }_1(\mathrm{t})\right)={\mathrm{A}}_1\sin \left({\omega }_1\mathrm{t}+{\phi }_1\right)\\ {\mathrm{u}}_2(\mathrm{t})={\mathrm{A}}_2\sin \left({\theta }_2(\mathrm{t})\right)={\mathrm{A}}_2\sin \left({\omega }_2\mathrm{t}+{\phi }_2\right)\end{array}$$

如果u1和u2的频率相同，则两者的相位差为初始相位之差。

两条曲线频率相同，最大值相同。因为相位不同，导致初始值不同。也就造成某个点时间的幅值不同。

$ \Delta $ $ \varphi $ = $ \varphi _ {1} $ - $ \varphi _ {2} $

$ \frac {\Delta \varphi }{2\pi } $ = $ \frac {\Delta t}{T} $

$ \Delta $ $ \varphi $ = $ \triangle $ t $ \frac {2\pi }{T} $ =2 $ \pi $ f $ \triangle $ t

由上式看到，在恒定延时情况下，相位差Δφ正比于信号频率f。

参考：
https://www.cnblogs.com/qiantuo1234/p/7460506.html