题目：

四平方和定理，又称为拉格朗日定理：

每个正整数都可以表示为至多4个正整数的平方和。

如果把0包括进去，就正好可以表示为4个数的平方和。

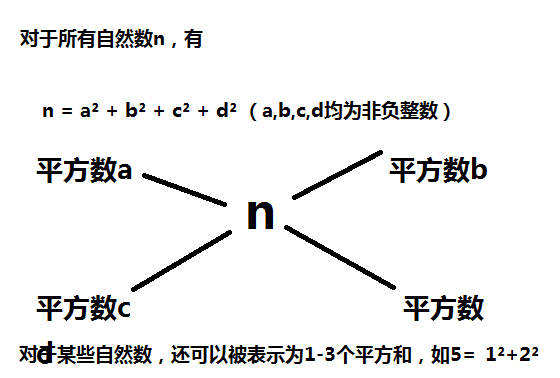
比如：

5 = 0^ 2 + 0^ 2 + 1^ 2 + 2^27 = 1^ 2 + 1^ 2 + 1^ 2 + 2^2
（^符号表示乘方的意思）

对于一个给定的正整数，可能存在多种平方和的表示法。

要求你对4个数排序：

0 <= a <= b <= c <= d

并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法

程序输入为一个正整数N (N<5000000)

要求输出4个非负整数，按从小到大排序，中间用空格分开

例如，输入：

5

则程序应该输出：

0 0 1 2

再例如，输入：

12

则程序应该输出：

0 2 2 2

再例如，输入：

773535

则程序应该输出：

1 1 267 838

分析：

因为题目只需要要一个升序排列的数列，那么我们让每一次循环的开始值都是上一个循环的结束点，这样我们就能确保是升序

首先要建三个循环，分别代表前三个数，那第四个数就是n减去前面三个数的开方，

第一个数的取值范围是n的开方，

第二个取值范围是n减去第一个数的开方

第三个取值范围是n减去第一个数和第二个数的开方

第四个 取值范围是n减去第一个数和第二个数及第三个数的开方

到最后如果四个加起来等于n那么直接输出并结束主函数。

步骤：

用到了math.sqrt开平方的函数

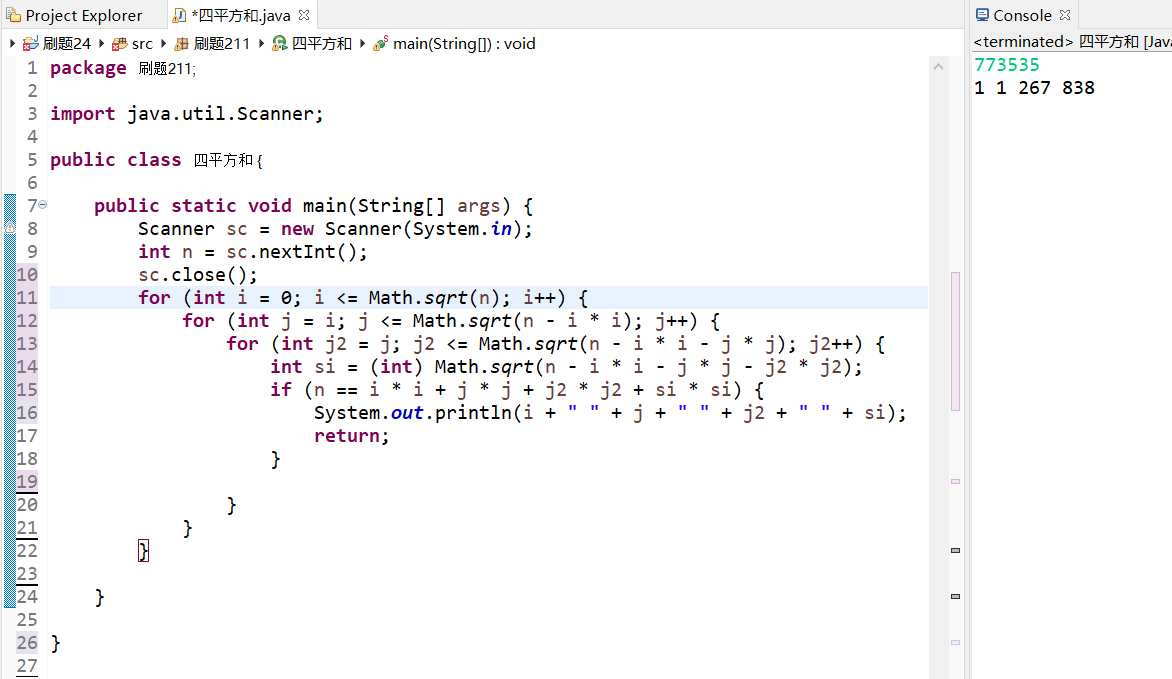
package 刷题211;

import java.util.Scanner;

public class 四平方和 {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        sc.close();
        for (int i = 0; i <= Math.sqrt(n); i++) {
            for (int j = i; j <= Math.sqrt(n - i * i); j++) {
                for (int j2 = j; j2 <= Math.sqrt(n - i * i - j * j); j2++) {
                    int si = (int) Math.sqrt(n - i * i - j * j - j2 * j2);
                    if (n == i * i + j * j + j2 * j2 + si * si) {
                        System.out.println(i + " " + j + " " + j2 + " " + si);
                        return;
                    }

                }
            }
        }
        
    }

}