文章目录
- 前言
- 一、直接插入排序算法
- 二、折半插入排序算法
- 三、2路插入排序算法
- 四、快速排序算法学习
前言
算法是道路生涯的一个巨大阻碍。今日前来解决这其中之一:有关的排序算法,进行实现以及性能分析。
一、直接插入排序算法
插入排序算法实现主要思想是将数据按照一定的顺序一个一个的插入到有序的表中,最终得到的序列就是已经排序好的数据。采用的方法是:在添加新的记录时,使用顺序查找的方式找到其要插入的位置,然后将新记录插入。
直接上代码实现下,学习代码比学习概念容易的多。
代码例子:对一个数组中的元素最终按照从小到大的顺序排列输出出来。
#include<stdio.h>
//自定义的输出函数
void print(int a[],int n,int i)
{
printf("%d:",i);
for(int j=0;j<8;j++)
{
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a[],int n)
{
for(int i=1;i<n;i++)
{
if(a[i]<a[i-1])//若第i个元素大于i-1元素则直接插入;反之,需要找到适当的插入位置后在插入
{
int j=i-1;
int x=a[i];
while(j>-1 && x<a[j])//采用顺序查找方式找到插入的位置,在查找的同时,将数组中的元素进行后移操作,给插入元素腾出空间。
{
a[j+1]=a[j];
j--;
}
a[j+1]=x;
}
print(a,n,i);
}
}
int main()
{
int a[4]={3,1,7,5};
InsertSort(a,4);
}
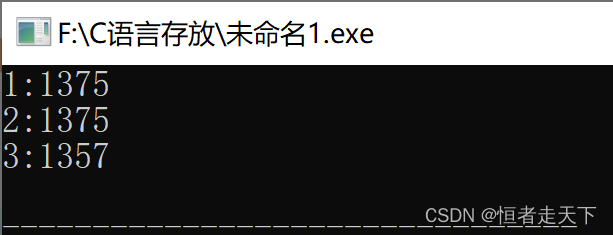
写完了代码也差不多了解了直接插入排序算法。比如上面我们写的代码实例是按照从小到大的顺序排序。
实现的时候,遍历所有元素,看看这个元素要插入的位置的前一个元素是否比它小,如果是的话直接插入。否则,,采用顺序遍历查找,向前遍历寻找这个元素要插入的位置,并且将数组中的元素都进行后移操作,给这个要插入的元素腾出空间。(元素的整体后移)
时间复杂度O(n^2)
二、折半插入排序算法
#include<stdio.h>
void print(int a[],int n,int i)
{
printf("%d:",i);
for(int j=0;j<n;j++)
{
printf("%d",a[j]);
}
printf("\n");
}
void BInsertSort(int a[],int size)
{
int i,j,low=0,high=0,mid;
int temp=0;
for(i=1;i<size;i++)
{
low=0;
high=i-1;
temp=a[i];
//采用折半查找法判断插入的位置,最终变量low表示插入位置
while(low<=high)
{
mid=(low+high)/2;
if(a[mid]>temp)
{
high=mid-1;
}
else
{
low=mid+1;
}
}
//有序表中插入位置后的元素统一后移
for(j=i;j>low;j--)
a[j]=a[j-1];
a[low]=temp;
print(a,8,i);
}
}
int main()
{
int a[8]={3,1,7,5,2,4,9,6};
BInsertSort(a,8);
}
这其实就是把上面的直接遍历换成了二分法寻找
折半插入排序算法相比较于直接插入排序 算法,只是减少了关键字间的比较次数,而记录的移动次数没有进行优化,所以时间复杂度仍然是O(n^2);
三、2路插入排序算法
2-路插入排序算法的具体实现思路为:另外设置一个同存储记录的数组大小相同的数组d,将无序表中第一记录添加进d[0]的位置上,然后从无序表中第二个记录开始,同的d[0]做比较:如果该值比d[0]大,则添加到其右侧;反之添加到其左侧。
接着用上面代码进行改版:
#include<stdio.h>
#include<stdlib.h>
void insert(int arr[],int temp[],int n)
{
int i,first,final,k;
first=final=0; //分别记录temp数组中最大值和最小值的位置
temp[0]=arr[0];
for(i=1;i<n;i++)
{
//待插入元素比最小的元素小
if(arr[i]<temp[first])
{
first=(first-1+n)%n;
temp[first]=arr[i];
}
//待插入元素比最大元素大
else if(arr[i]>temp[final])
{
final=(final+1+n)%n;
temp[final]=arr[i];
}
//插入元素比最小大,比最大小
else
{
k=(final+1+n)%n;
//当插入值比当前值小时,需要移动当前值的位置
while(temp[((k-1)+n)%n]>arr[i])
{
temp[(k+n)%n]=temp[(k-1+n)%n];
k=(k-1+n)%n;
}
//插入该值
temp[(k+n)%n]=arr[i];
//因为最大值的位置改变,所以需要实时更新final的位置
final=(final+1+n)%n;
}
}
//将排序记录复制到原来的顺序表里
for(k=0;k<n;k++)
arr[k]=temp[(first+k)%n];
}
int main()
{
int a[8]={3,1,7,5,2,4,9,6};
int temp[8];
insert(a,temp,8);
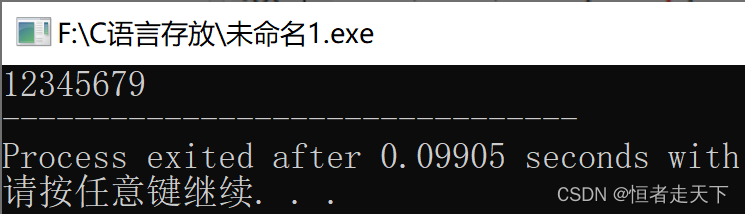
for(int i=0;i<8;i++)
printf("%d",a[i]);
return 0;
}
四、快速排序算法学习
快速排序算法实现的基本思想是:通过一次排序将整个无序表分成相互独立的两部分,其中一部分中的数据都比另一部分中包含的数据的值小,然后继续沿用此方法分别对两部分进行同样的操作,直到每一个小部分不可再分,所得到的整个序列就成为了有序序列。
具体步骤如下:
(1)先从数列中取出一个元素作为基准数
(2)扫描数列,将比基准数小的元素全部放到它的左边,大于或等于基准数的元素全部放到它的右边,得到左右两个区间。
(3)再对左右区间重复第二步,直到各区间少于两个元素。
接下来通过图片展示一次这个步骤,相信剩下的应该也就理解了。
如下实例:
(1)以数组的第一个元素作为基准数,取出来,进行另存
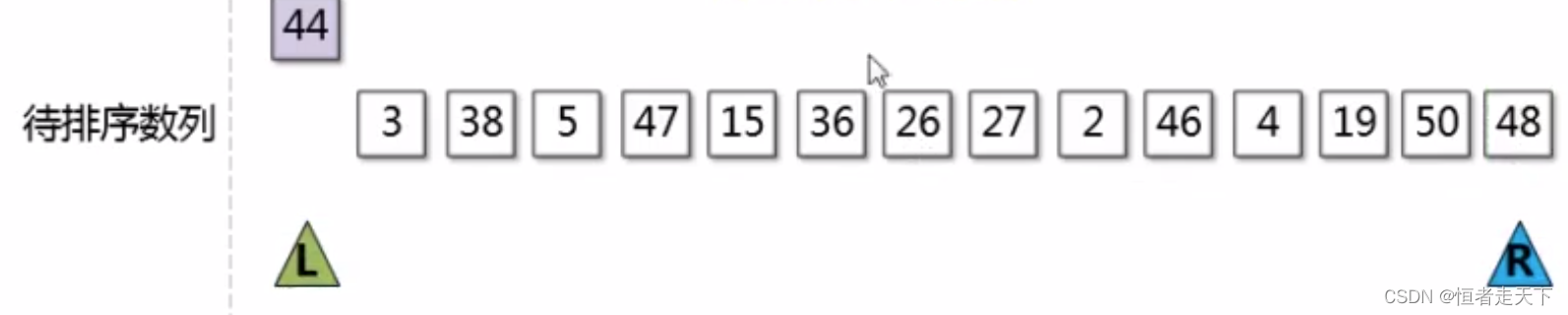
(2)从区间的最右边找个比这个基准数小 的数,放到 它这个位置,如下图是找到了19.

放到原基准数的位置

(3)然后再在区间的最左边开始找比基准数大的元素找到了就放到R空的那个位置
如下图是找到了47

放到R空的位置

(4)如此这么循环,直到L和R相遇,把这个基准数填到相遇的位置

这样基准数的左边都比基准数小,基准数右边的都比基准数大。
如此这么递归,把所有区间递归完,即排完序了。
接下来我们看下代码:
代码实例中,我特地没在数组的第一个位置存储元素,特地用它来存储这个移出来,等待插入的基准数
#include<stdio.h>
#include<stdlib.h>
#define MAX 9
//单个记录的结构
typedef struct
{
int key;
}SqNote;
//记录表的结构体
typedef struct
{
SqNote r[MAX];
int length;
}SqList;
int Partition(SqList *L,int low,int high)
{
L->r[0]=L->r[low]; //下标为0的位置存放提取出来的基节点
int pivotkey=L->r[low].key;
//直到两指针相遇,程序结束
while(low<high)
{
//high指针左移,直到遇到比pivotkey值小的记录,指针停止移动
while(low<high && L->r[high].key>=pivotkey)
{
high--;
}
//直接将high指向的小于支点的记录移动到low指针的位置
L->r[low]=L->r[high];
//low指针右移,直到遇到比pivotkey值大的记录,指针停止移动
while(low<high && L->r[low].key<=pivotkey)
{
low++;
}
//直接将low指向的大于支点的记录移动到high指针的位置
L->r[high]=L->r[low];
}
//将支点添加到准确的位置
L->r[low]=L->r[0];
return low;
}
void QSort(SqList *L,int low,int high)
{
if(low<high)
{
//找到支点的位置
int pivotloc=Partition(L,low,high);
//对支点左侧的子表进行排序
QSort(L,low,pivotloc-1);
//对支点右侧的子表 进行排序
QSort(L,pivotloc+1,high);
}
}
void QuickSort(SqList *L)
{
QSort(L,1,L->length);
}
int main()
{
SqList *L=(SqList*)malloc(sizeof(SqList));
L->length=8;
L->r[1].key=49;
L->r[2].key=38;
L->r[3].key=65;
L->r[4].key=97;
L->r[5].key=76;
L->r[6].key=13;
L->r[7].key=27;
L->r[8].key=49;
QuickSort(L);
for(int i=1;i<=L->length;i++)
printf("%d",L->r[i].key);
return 0;
}
快速排序算法的时间复杂度为O(nlogn),是所有时间复杂度相同的排序方法中性能最好的排序算法。