day35|01背包问题、416. 分割等和子集

news2024/12/24 0:01:24

01背包问题

有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

例：背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

一、二维dp数组01背包

1、确定dp数组以及下标的含义

dp[i][j]：在下标[0,i]的物品任取，放进容量为j的背包，价值总和最大是多少

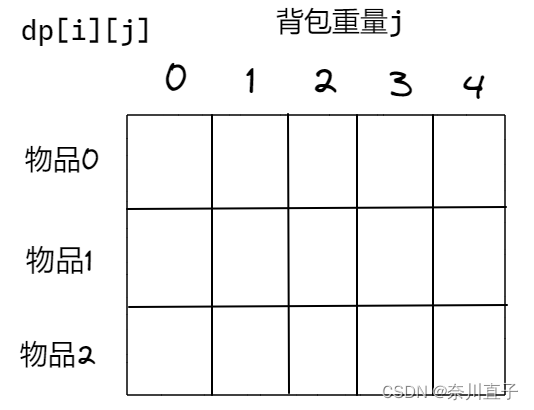
2、确定递推公式

如果背包重量小于物品 i 的重量，那么就不把 i 放进背包里，可得

所以递推公式为：

dp[i][j]=dp[i-1][j]

如果背包重量大于物品i的重量，分类讨论：
- 放物品i：dp[i][j]=dp[i-1][j-weight[i]]+value[i]
- 不放物品i：dp[i][j]=dp[i-1][j]

所以递推公式为：

dp[i][j]=Math.max(dp[i-1][j-weight[i]]+value[i],dp[i-1][j])

3、dp数组初始化

① 根据dp的递推公式dp[i-1][j]可知，i 由i-1推导出来(上面的元素)，所以要初始化i=0时的数组元素，即dp[0][j]，存放编号为0的物品时，放入各个重量的状态，最大价值总和。

当weight[0]>j 时，dp[0][j]=0。背包容量比编号0的物品重量还小

当weight[0]<=j 时，dp[0][j]=value[0]。背包容量放足够放编号0物品

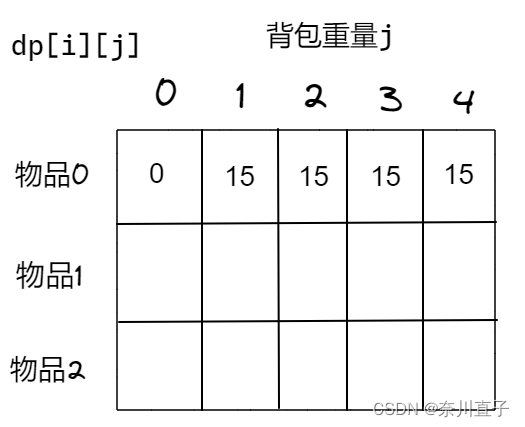
② 根据dp[i-1][j-weight[i]]+value[i]可知，j 由j-weight[i] 推导出来(左上角的元素)，所以要初始化j=0时的元素，即dp[i][0]=0，背包重量为0，放不进去，所以最大价值为0。

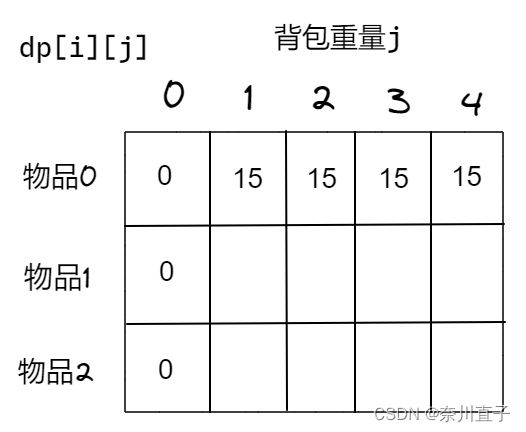
其它元素随意赋初始值，因为会被覆盖。

4、确定遍历顺序

先遍历物品（先横向遍历）或者先遍历重量（先遍历纵向）都可以，都可以保证左上方和上方已有值。

5、举例推导dp数组

public class Main {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 动态规划获得结果
     * @param weight  物品的重量
     * @param value   物品的价值
     * @param bagSize 背包的容量
     */
    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods][bagSize + 1];

        // 初始化dp数组
        // 创建数组后，其中默认的值就是0
        //i=0,dp[0][j]
        for (int j = 0; j <= bagSize; j++) {

            if (weight[0]>j){
                dp[0][j]=0;
            }
            else if (weight[0]<=j){
                dp[0][j]=value[0];
            }
        }
        
        //j=0,dp[i][0]
        for (int i = 0; i < goods; i++) {
            dp[i][0] = 0;
        }

        // 填充dp数组
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i-1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }

        // 打印dp数组
        for (int i = 0; i < goods; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}

二、一维dp数组01背包（滚动数组）

行覆盖。把dp[i - 1]那一层拷贝到dp[i]上，只用一维数组dp[j]

1、确定dp数组以及下标的含义

dp[j]：容量为j的背包，所背的物品价值可以最大为dp[j]。

2、一维dp数组的递推公式

不放物品 i 时，dp[j]=dp[j]（相当于dp[i-1][j]）
放物品 i 时，dp[j]=dp[j-weight[i]]+value[i]

递推公式为：

dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i])

3、一维dp数组初始化

题目给的价值都是正整数，那么非0下标都初始化为0。dp[j]=0

这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

4、一维dp数组遍历顺序

① 倒序，背包从大到小，为了保证物品i只被放入一次。

例：物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历，假设i=0时

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

倒序就是先算dp[2]

dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

dp[1] = dp[1 - weight[0]] + value[0] = 15

tips：假设目前有背包容量为10，可以装的最大价值，记为g[10]。即将进来的物品重量为6。价值为9。

如果不装该物品，显然背包容量无变化，这里对应二维数组，其实就是取该格子上方的格子复制下来，就是所说的滚动下来，直接g[10[ = g[10]，这两个g[10]要搞清楚，右边的g[10]是上一轮记录的，也就是对应二维数组里上一层的值，而左边是新的g[10]，也就是对应二维数组里下一层的值。

如果装该物品，则背包容量= g[10-6] = g[4] + 9 ，也就是 g[10] = g[4] + 6 ,这里的6显然就是新进来的物品的价值，g[10]就是新记录的，对应二维数组里下一层的值，而这里的g[4]是对应二维数组里上一层的值，通俗的来讲：你要找到上一层也就是上一状态下背包容量为4时的能装的最大价值，用它来更新下一层的这一状态，也就是加入了价值为9的物品的新状态。

这时候如果是正序遍历会怎么样？g[10] = g[4] + 6 ，这个式子里的g[4]就不再是上一层的了，因为你是正序啊，g[4] 比g[10]提前更新，那么此时程序已经没法读取到上一层的g[4]了，新更新的下一层的g[4]覆盖掉了，这里也就是为啥有题解说一件物品被拿了两次的原因。

② 先遍历物品再遍历背包容量

如果顺序反了，dp[j]就会一直为最大值，最终结果为30，30，30，30，30

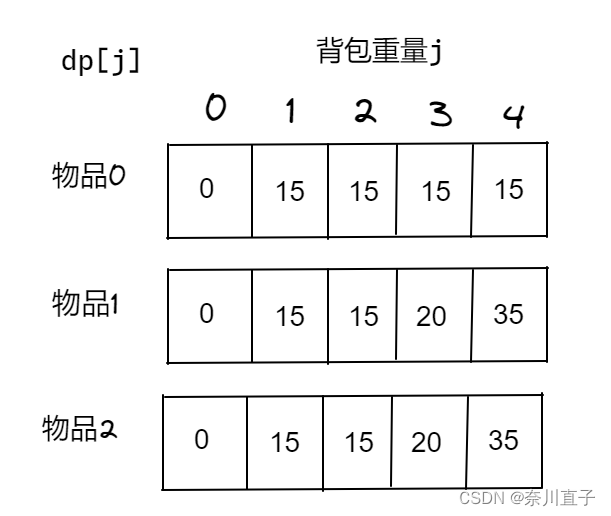
5、举例推导dp数组

一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下：

public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagWight = 4;
        testWeightBagProblem(weight, value, bagWight);
    }

    public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
        int wLen = weight.length;
        //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
        int[] dp = new int[bagWeight + 1];
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 0; i < wLen; i++){
            for (int j = bagWeight; j >= weight[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        //打印dp数组
        for (int j = 0; j <= bagWeight; j++){
            System.out.print(dp[j] + " ");
        }
    }