题目描述

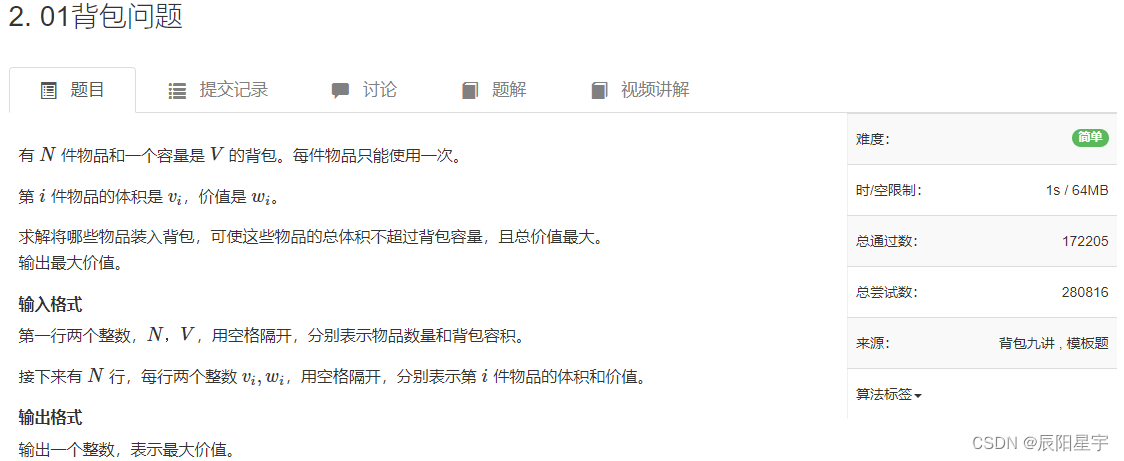
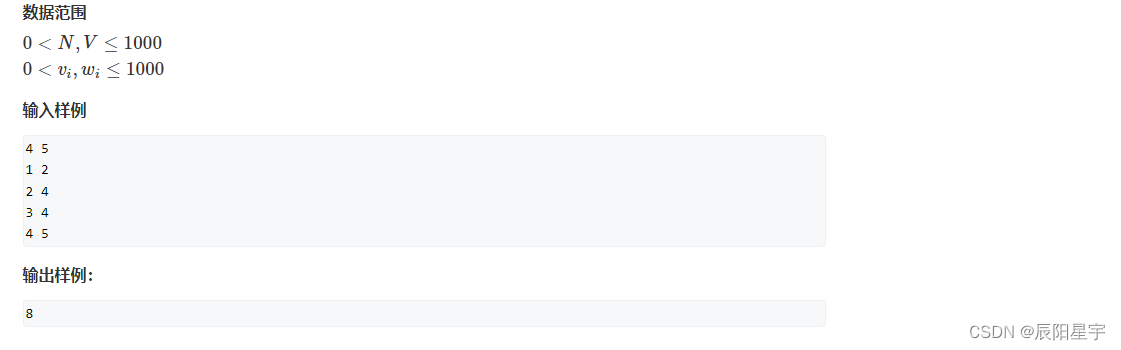
在这里插入图片描述

原题链接：2. 01背包问题

解题思路

（1）二维dp数组

动态规划五步曲：

（1）dp[i][j]的含义： 容量为j时，从物品1-物品i中取物品，可达到的最大价值

（2）递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])，其中dp[i - 1][j]表示不放物品i时的最大价值；j - v[i]表示给物品i留出空间，dp[i - 1][j - v[i]]表示给物品i留出空间后，放入其余物品可达到的最大价值（由于是按物品递增顺序遍历，因此为从1-i-1的物品），dp[i - 1][j - v[i]] + w[i]表示放入物品i和其余放入其余物品，可到达的最大价值。

（3）dp数组初始化： dp[0][j] = d[i][0] = 0, dp[0][j]中j >= v[i]的取w[i]

（4）遍历顺序： 从小到大，先背包后物品，或先物品后背包都可以。

（5）举例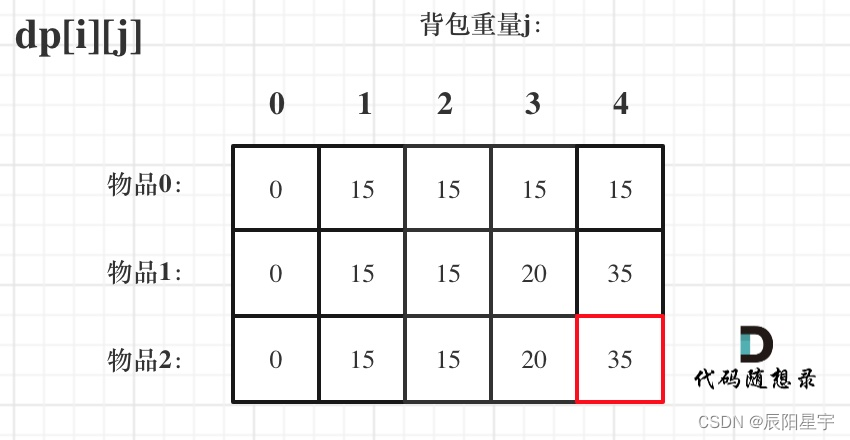： **加粗样式**

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int dp[N][N];

int main(){

    int n, m;
    int v[N], w[N];
    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            // 当前物品重量大于背包容量时，不放该物品
            if(j < v[i])        dp[i][j] = dp[i - 1][j];
            // 当前物品重量小于等于背包容量时，在放该物品后和不放该物品之间选择一个最大价值
            else                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
        }
    }
    
    cout << dp[n][m] << endl;
    
    return 0;
}

（2）优化为一维dp数组（滚动数组）

滚动数组含义：本轮所计算的数，需要用到上一轮的结果，依次类推，滚动计算。

优化成一维那就要在遍历上实现与二维相同的逻辑顺序，从而实现仅用一维就可以代替二维。

动态规划五步曲：

（1）dp[j]数组的含义： 容量为j时，装入的物品可达到的最大价值。

（2）递推公式： dp[j] = max(dp[j], dp[j - v[i]])

（3）dp数组初始化： dp[0] = 0

（4）遍历顺序： 两层for循环，先遍历物品，再遍历背包，内层按背包从大到小递减顺序遍历。
如果删除dp中的维度[i]后，还保持对j的从小到大遍历，那么此时的代码其实是等价于dp[i][j] = max(dp[i][j - 1], dp[i][j - v[i])，在一遍后续遍历中，因为j是从小到大与v[i]相减，在后续相减时，可能会出现本轮遍历中用过的数，会使之前使用过的数重复相加。

而如果以对j进行从大到小遍历，因为此时是j是从m到v[i]，以此顺序计算dp[j - v[i]]时，在一遍后续遍历中，都是会基于上一轮对i的遍历而进行判定，并且由于j变化而v[i]不变，在后续不会出现使用过的数重复相加。每次遍历到的j所对应dp[j - v[i]]都还没有被更新，就相当于是之前的状态dp[i - 1][j - v[i]]，从而得到dp[j] = dp[j - v[i]]就等价于dp[i][j] = dp[i - 1][j - v[i]]。

（5）举例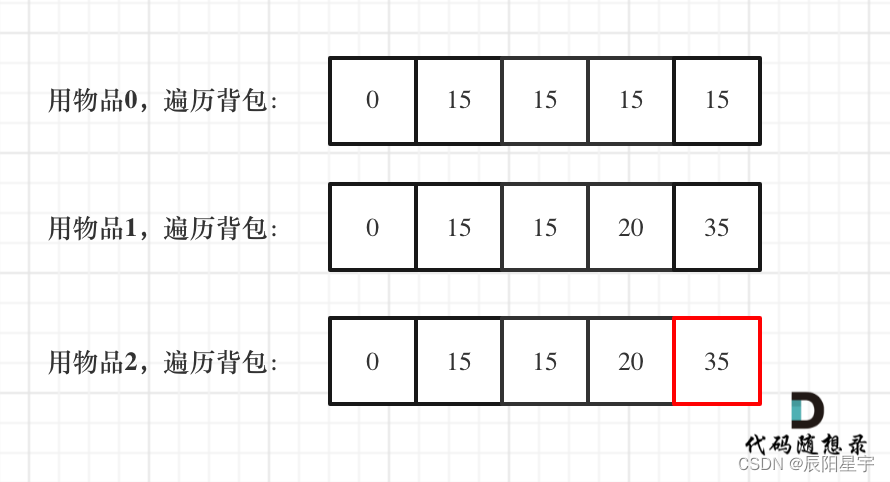： 在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int dp[N];

int main(){

    int n, m;
    int v[N], w[N];
    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        // 从后向前遍历，表示装入一个物品后，剩余的可装入容量达到的最大价值
        for(int j = m; j >= v[i]; j--) {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    
    return 0;
}