从0开始的秋招刷题路，记录下所刷每道题的题解，帮助自己回顾总结

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

示例 1：

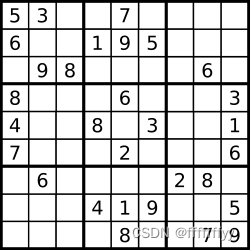
输入：board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出：[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

提示：
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解

用 DFS 的回溯法求解从树的根节点 []开始按照深度逐个遍历

回溯法算实际上就是一个决策树（因为在每个节点上都要做决策）的遍历过程：

路径：也就是已经做出的选择。
选择列表：也就是当前可以做的选择。
结束条件：也就是到达决策树底层(选择列表为空的时候)，无法再做出选择的条件。
算法对每一个空着的格子穷举 1 到 9，如果遇到不合法的数字（在同一行、同一列、同一个 3×3 的区域中存在相同的数字）则跳过，如果找到一个合法的数字，则继续穷举下一个空格子。

对于每个位置，从 1 到 9 就是做选择，全部试一遍即可（消耗时间太多）。

对第一行中的每个格子从 1 到 9 进行遍历，当 j 超过每一行的最后一个索引时，即 j==n 时，转为增加 iii 开始遍历下一行重新开始，并在 “做选择” 之前添加一个判断，跳过不满足条件的数字。

// 到达该行的末尾，则换到下一行重新开始
if (j == n) return backtrack(board, i + 1, 0);
若当前遍历的位置上是预先设置数字，即 board[i][j]!= ’ . ’ 时，此时不需要进行任何操作直接跳过该位置，进行下一个格子的判断。

// 当前遍历的位置上有预先设置好的数字，则继续遍历下一个位置
if (board[i][j] != ‘.’) return backtrack(board, i, j + 1);
剪枝
若当前遍历位置 board[row][col]在棋盘的 row 这一行中有相同的数字或在棋盘的 col 这一列中有相同的数字或 board[row][col] 所在的 3×3 的方框中有重复的数字，此时需要进行 <剪枝> 操作，直接跳过该数字，继续下一个数字的遍历即可。

public boolean isValid(char[][] board, int row, int col, char c) {

    for (int i=0;i<9;i++) {

        if (board[row][i] == c) return false; // row 
        if (board[i][col] == c) return false; // col
        if (board[(row / 3 * 3 + i / 3)][(col / 3) * 3 + i % 3] == c) { // 3 × 3

            return false;
        }
    }
    return true;
}

if (!isValid(board, i, j, c)) continue; // 剪枝

当在 “做选择” 时，就是从 “选择列表” 中拿出一个 “选择”，并将它放入到 “路径” 中。

遍历 111 到 999 的数字，若当前遍历的数字通过了 <剪枝> 操作，则令 board[i][j]=c 并且令 j+1 继续遍历下一个位置。

结束条件：当 i==m 时，说明已经遍历完了最后一行，完成了所有穷举，此时就是一个可行解，直接回溯到上一层，并将回溯之前位置上的数字拿掉，即 board[i][j]= ’ . '（回溯到上一层后，继续遍历选择列表，选择下一个分支）（“撤销选择”：就是从 “路径” 中拿出一个选择，将它恢复到 “选择列表” 中）即可。

注意：题目要求只有一个解而不是要所有合法的答案，为了减少时间复杂度，可以让 backtrack() 方法的返回值为 boolean类型，如果找了一个可行解就返回 true，这样就可以阻止后续的递归，最终只找到一个可行解并且会大大降低时间复杂度。

代码

class Solution {

    public void solveSudoku(char[][] board) {

        backtrack(board, 0, 0);
    }

    public boolean isValid(char[][] board, int row, int col, char c) {

        for (int i=0;i<9;i++) {

            if (board[row][i] == c) return false; // row 
            if (board[i][col] == c) return false; // col
            if (board[(row / 3 * 3 + i / 3)][(col / 3) * 3 + i % 3] == c) { // 3 × 3

                return false;
            }
        }
        return true;
    }

    public boolean backtrack(char[][] board, int i, int j) {

        int m = 9, n = 9;
        // 到达该行的末尾，则换到下一行重新开始
        if (j == n) return backtrack(board, i + 1, 0);

        if (i == m) return true; // 结束条件

        // 当前遍历的位置上有预先设置好的数字，则继续遍历下一个位置
        if (board[i][j] != '.') return backtrack(board, i, j + 1);

        for (char c='1';c<='9';c++) {

            if (!isValid(board, i, j, c)) continue; // 剪枝

            board[i][j] = c; // 做选择

            if (backtrack(board, i, j + 1)) return true;

            board[i][j] = '.'; // 撤销选择
        }
        return false;
    }
}