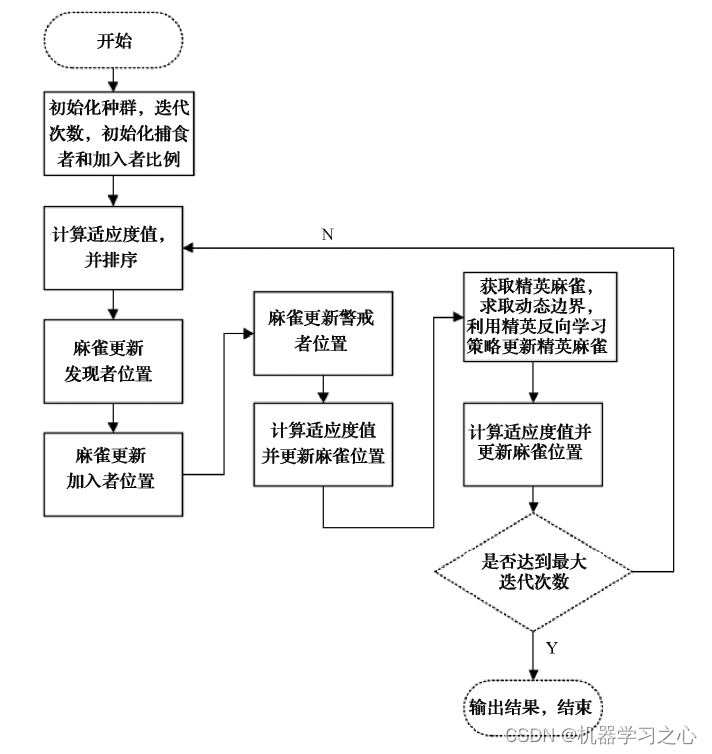
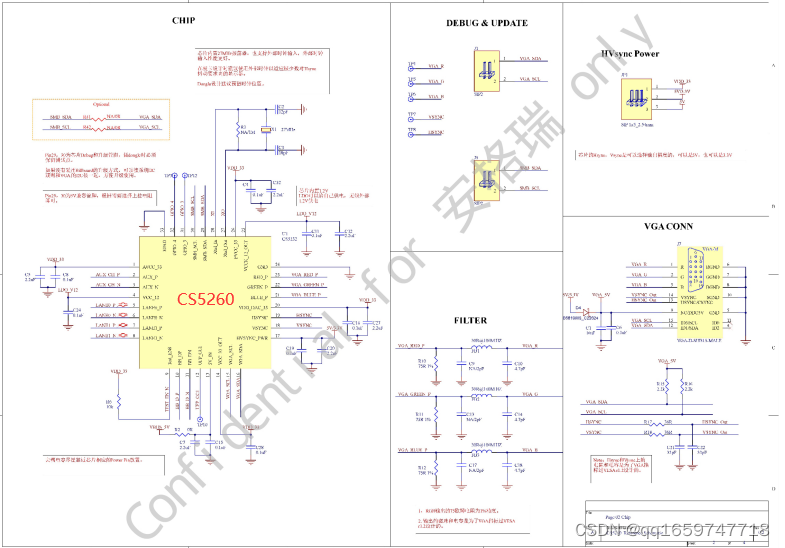
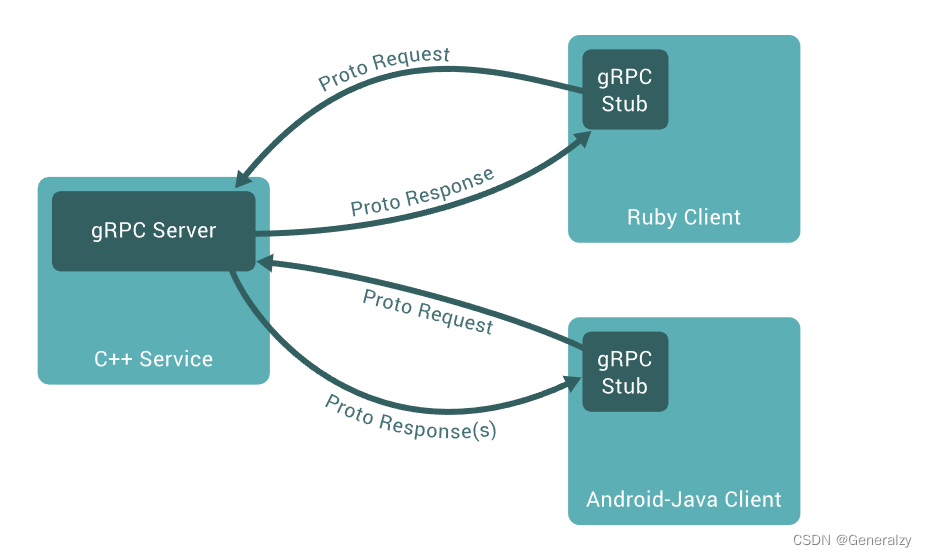
在看MSC-VO代码的过程中,大量出现了奇异值分解的内容,本身对这部分了解不多,这里补一下课,参考b站up主小旭学长的视频,链接为:PCA主成分分析和SVD主成分分析
PCA主成分分析
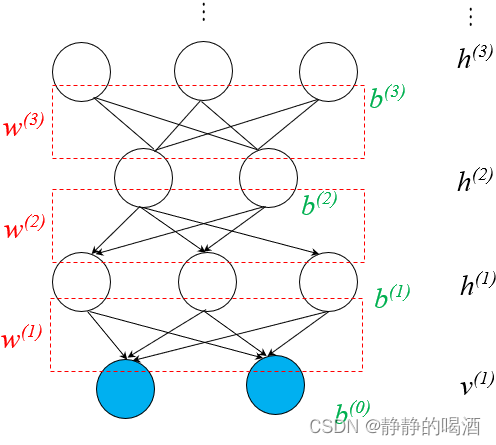
PCA根本目的在于让数据在损失尽可能小的前提下,降低数据的维度。比如将三维数据降低到二维,那么就是要在空间中找一个平面,让3d点在2d平面上的投影尽可能保持原来3d空间下的分布。将这个概念推广一下,PCA的任务也就是找一个新的坐标系,让原数据在新坐标系下的投影损失尽可能小,而这个新的坐标系的寻找方法,我们就要依赖于方差这一概念。这里我们可以这样去理解,方差衡量的是数据的密集程度,方差小意味着这一大堆数据几乎就是集中在一小撮,这样必然会导致数据的差异性变得很模糊,因此我们在进行降维时,需要寻找的坐标系最好是方差尽可能大的,从而能让数据降维后分布尽量分散。因此这里我们要寻找的这个坐标系,就是原数据中方差最大的方向。

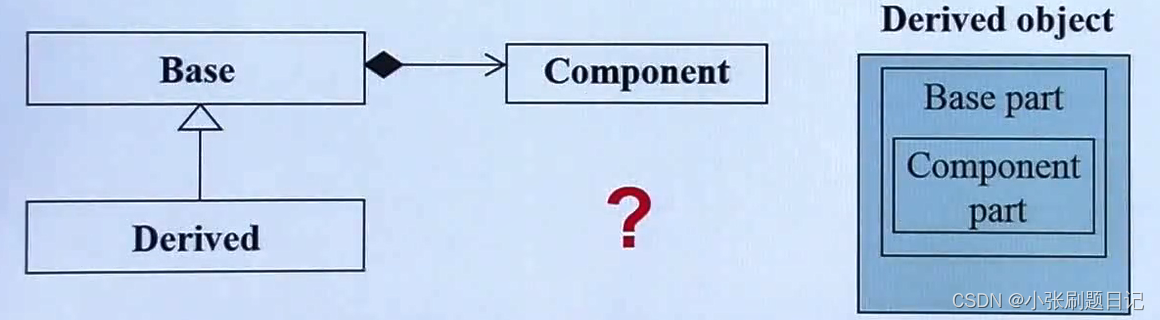
在进行坐标系的寻找之前,我们需要对原始数据做一个中心化的操作,也就是将坐标原点移动到数据的分布中心,这主要是为了更好地寻找方差最大的方向。移动到中心后,就需要进行一系列的推导,这里我们假定最后的处理结果数据符合高斯分布,根据线性代数中数据的拉伸和旋转的写法,拉伸等于左乘一个对角阵,旋转等于左乘一个三角函数构成的矩阵,数据的处理前后本身就可以用旋转和拉伸来表示。
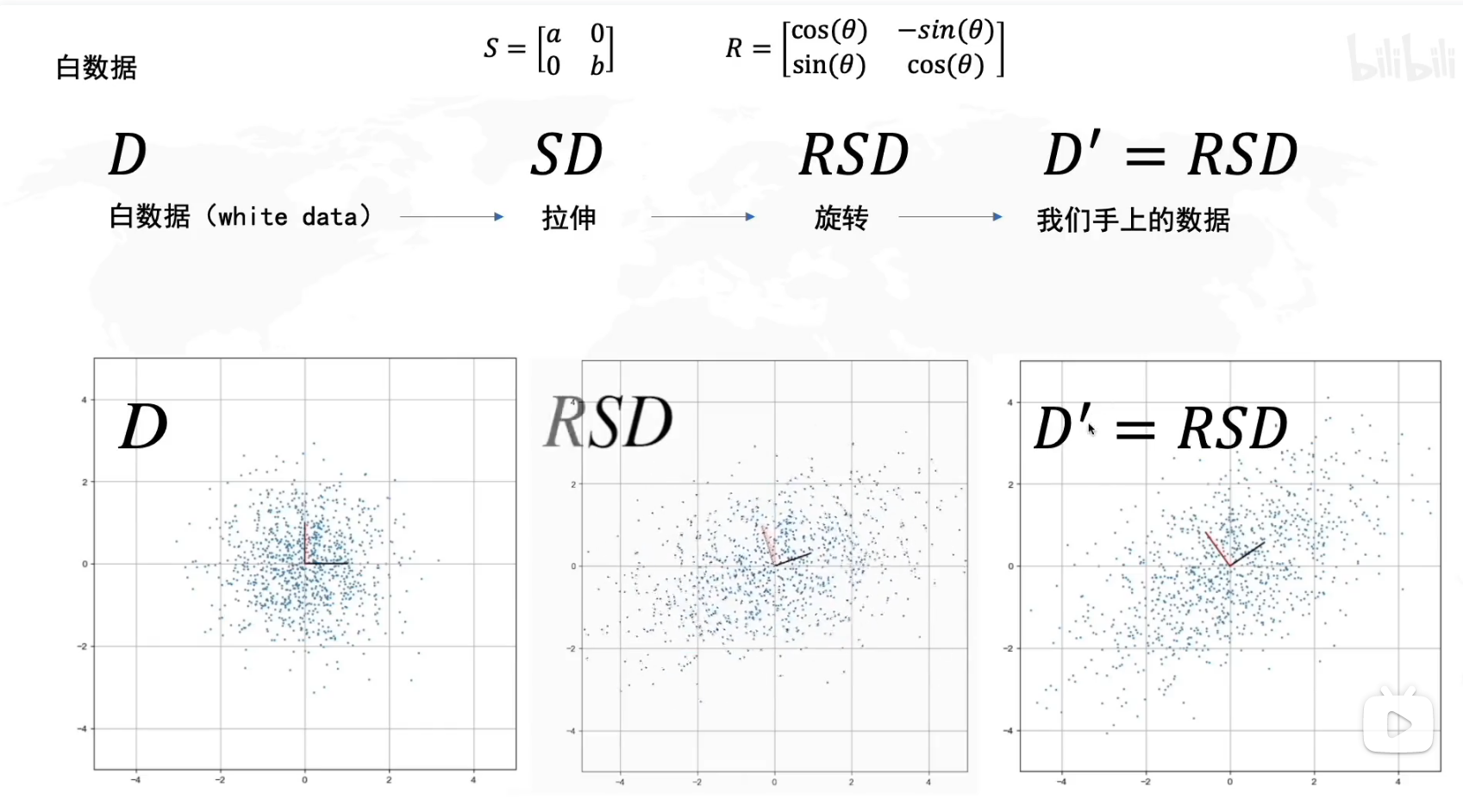
上图描述的是原始数据和最终结果之间通过旋转和拉伸的转换关系,在这个问题中,我们并不知道旋转和拉伸的幅度,所以问题变为如何求R和S。在求R和S的过程中,我们需要利用协方差矩阵COV,协方差用于表示两个变量在变化过程中的关联关系,协方差为正表示两个量是正相关,反之为负相关,如果为零则表示两个量相互无关。根据协方差矩阵的定义,我们可以得到下面的化简公式:
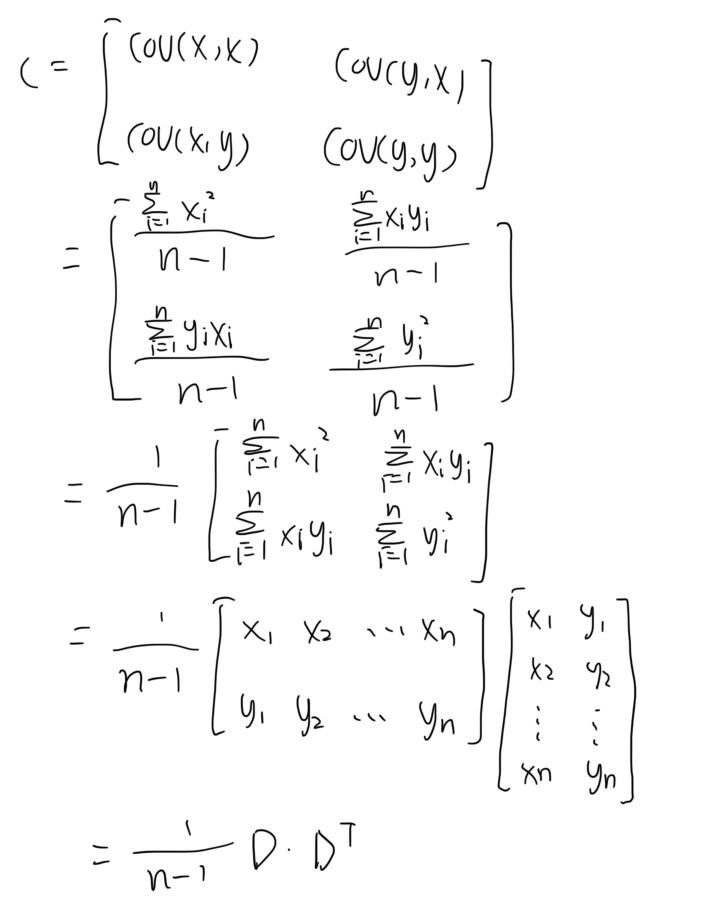
从这个公式可以看出,协方差矩阵的计算依赖于原数据构成的矩阵,这里为了方便我们统一以二维举例,那么最后的x1 x2 y1 y2表示的就是二维坐标下的点,我们将其记录为数据矩阵D。而在前面我们得到了原始数据和处理结果之间基于旋转R和拉伸S的转换关系,那么带入后可以继续往后写。
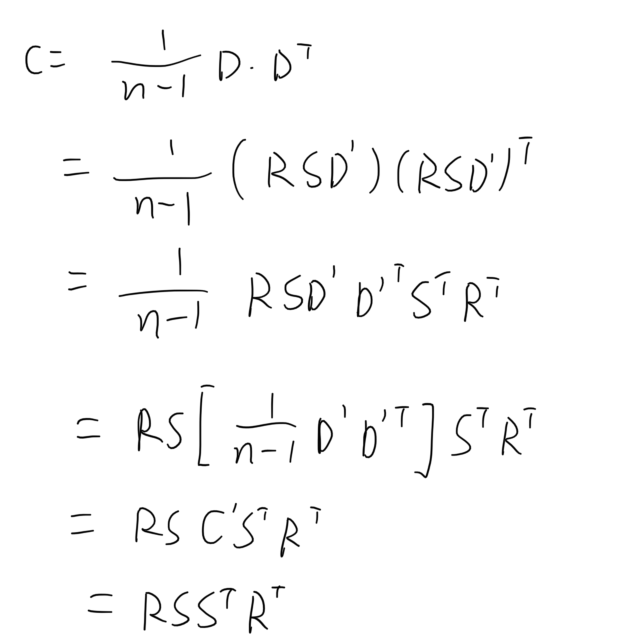
在这个过程中主要有这么几步需要解释一下,首先右上角加’表示的是最终结果,这个与前面的推导稍微有点不同但是一个意思。在第四行,括号内对应的刚好是目标坐标系的协方差矩阵,因此括号的内容在第五行合成为了C’,由于前面我们假定了目标坐标系的数据在两个方向都符合高斯分布,所以协方差矩阵为单位矩阵,所以在第六行可以直接消去C’,从而得到最后的计算结果。由于S本身是一个对角阵,因此转置与否都不发生变化,而且R本身是一个正交矩阵,R的转置与逆矩阵相等,所以我们进行如下的操作。
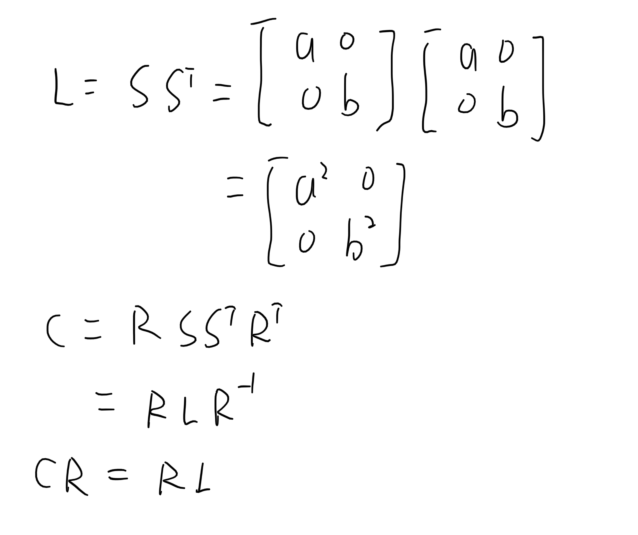
从最终结果来看,这个结果其实对应了考研数学中老生常谈的矩阵对角化,C表示的是原始数据的协方差矩阵,L本身为对角阵,因此就是由特征值组成的对角矩阵,R则为特征向量拼成的矩阵。所以我们要求R和S,就需要先计算原始数据的协方差矩阵,对这个矩阵做对角化,结果的特征向量组成的矩阵就是旋转R,特征值对角阵开方得到的就是拉伸S。
SVD奇异值分解
SVD本身和矩阵对角化是相通的,矩阵对角化要求矩阵必须是一个方阵,这个时候可以计算出特征值和特征向量,而当矩阵本身不是方阵时,我们就无法计算特征值与特征向量,与之相对应的就变成奇异值,当矩阵为方阵的时候,奇异值和特征值就是一个东西。类似于对角化,奇异值分解本身也是要寻找矩阵,由于不是方阵,这里目标变成了三个矩阵。
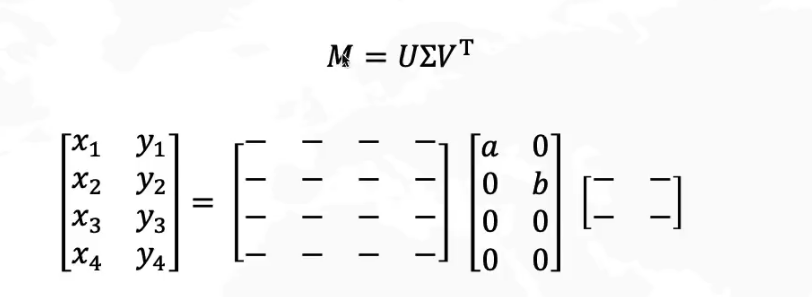
奇异值分解的过程本身也可以用拉伸旋转的理论来解释,我们将M看作是一个线性变换,我们希望找到一个基,这个基在线性变换前后依然可以保持正交,这个就是SVD的主要任务。假设V是原始域的标准正交基,U是经过M变换后的标准正交基,由于SVD本身要求变换前后保持正交即可,所以结果的U不一定是标准正交基,这里额外补充一个伸缩б1和б2用于实现这个正交的对齐。那么我们可以写出下面的等式:
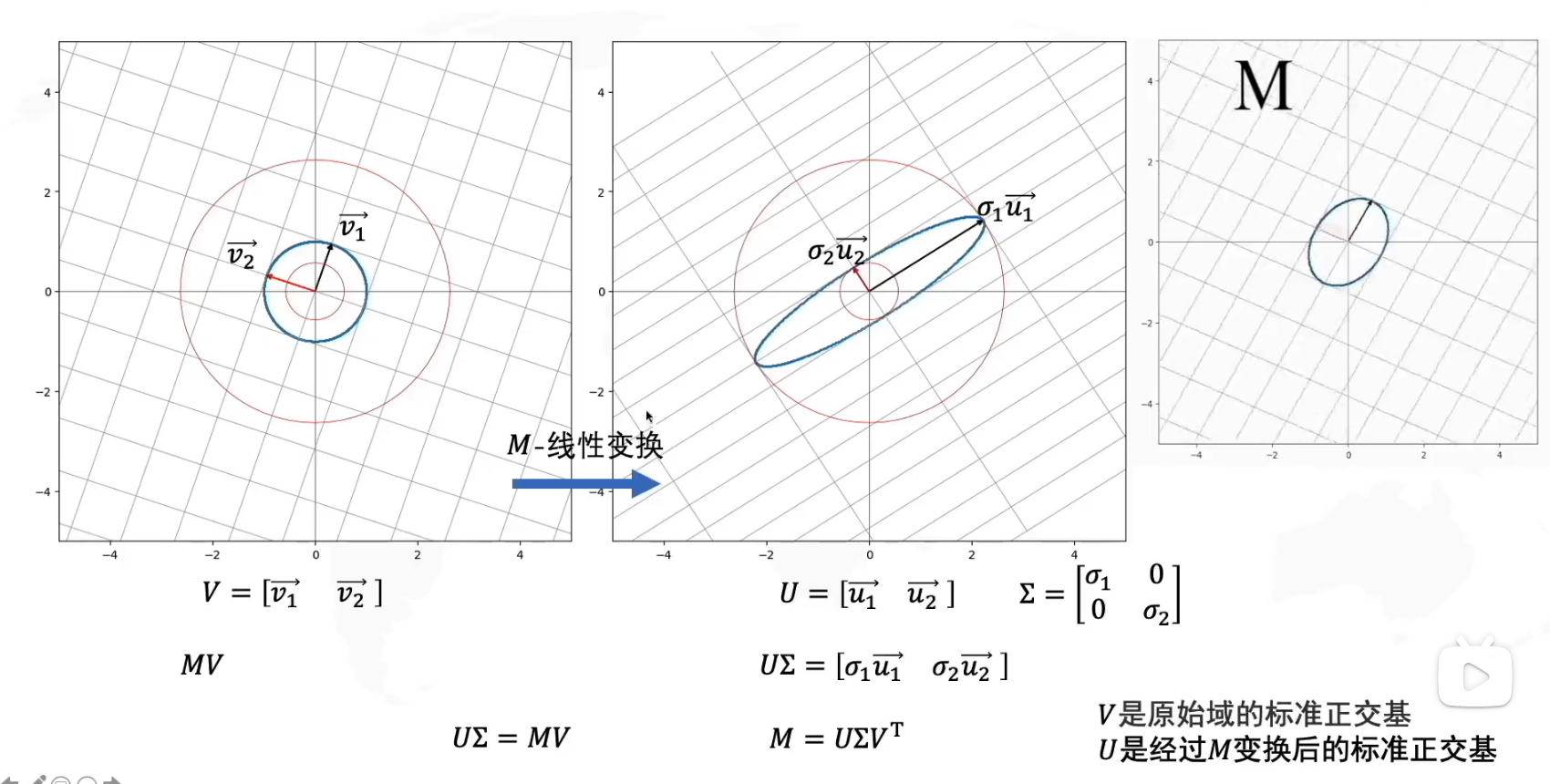
得到了M的表示,那么我们可以继续进行后续的推理:

在这部分公式中,左侧第三行到第四行中,由于U本身表示的是标准正交基组成的矩阵,其转置右乘原矩阵等于单位矩阵,因此在这一步中进行了消去,第四行中的操作和前面PCA的过程基本相似,∑本身不一定是方阵,但其依然符合主对角线上有元素其余位置均为零,所以依然可以整合为一个平方的矩阵,这里就是记作了L,也就是到了第五行的位置,在第五行中,L已经变成了一个方阵,公式左侧也是一个方阵,这时等式的形式就转变为了矩阵对角化的结果,左侧是原矩阵,右侧的L为特征值组成的对角矩阵,V表示特征向量组成的矩阵,所以对MTM和MMT分别进行对角化,就可以计算出线性变化前后的两个基底,对特征值矩阵进行开方,就可以得到伸缩系数。

PCA与SVD的关系
在PCA中我们需要的旋转R和SVD中的V是一样的,也就是说SVD的V就是PCA的主成分的方向。
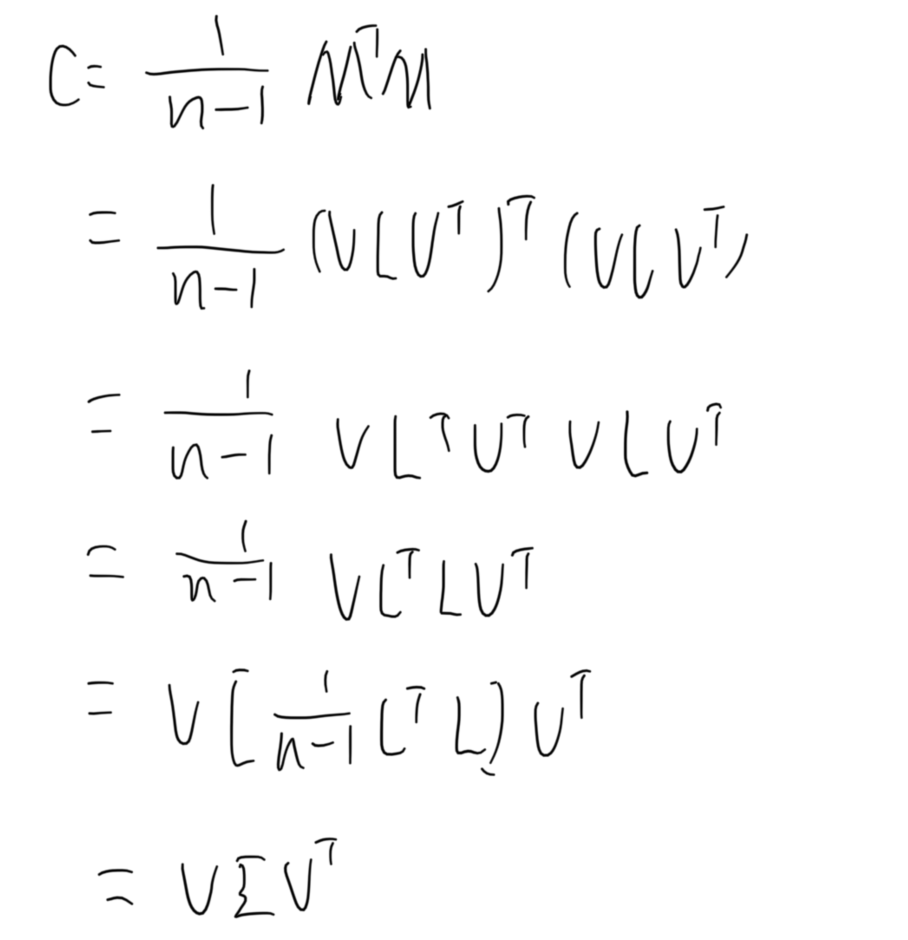
这二者之间的关系主要通过这个V矩阵进行联系,PCA需要先计算协方差矩阵,计算量可能会比较大,反过来用SVD的话,可以不计算协方差矩阵直接求出V。