引言

上一节介绍了从监督学习、无监督学习任务的角度介绍了经典模型。本节将从表示、推断、学习三个任务出发，继续介绍生成模型。

生成模型的表示任务

从形状的角度观察生成模型的表示任务

关于概率生成模型，从形状的角度，我们介绍更多的是概率图结构：

• 从概率图结构内部的随机变量结点出发，可以将随机变量划分为两种类型：

  • 离散型随机变量($\text{Discrete Random Variable}$)
  • 连续型随机变量($\text{Continuous Random Variable}$)

  例如高斯混合模型($\text{Gaussian Mixture Model,GMM}$)，它的概率图结构表示如下：
  
  其中隐变量$\mathcal{Z}$是一个一维、离散型随机变量，它的概率分布$\mathcal{P}(\mathcal{Z})$可表示为：
  这里假设$\mathcal{Z}$服从包含$\mathcal{K}$种分类的$\text{Categorial}$分布。
  P ( Z ) = { P 1 , P 2 , ⋯   , P K } ∑ k = 1 K P k = 1 \mathcal P(\mathcal Z) = \{\mathcal P_1,\mathcal P_{2},\cdots,\mathcal P_{\mathcal K}\} \quad \sum_{k=1}^{\mathcal K} \mathcal P_{k}= 1 P(Z)={P1​,P2​,⋯,PK​}k=1∑K​Pk​=1
  当隐变量$\mathcal{Z}$确定的条件下，对应的观测变量$\mathcal{X}$是一个服从高斯分布($\text{Gaussian Distribution}$)的连续型随机变量。
  关于$\mathcal{X}$的维度，有可能是一维，也有可能是高维。均可用高斯分布进行表示。
  P ( X ∣ Z ) ∼ N ( μ k , Σ k ) k ∈ { 1 , 2 , ⋯   , K } \mathcal P(\mathcal X \mid \mathcal Z) \sim \mathcal N(\mu_{k},\Sigma_{k}) \quad k \in \{1,2,\cdots,\mathcal K\} P(X∣Z)∼N(μk​,Σk​)k∈{1,2,⋯,K}

• 从连接随机变量结点的边观察，也可以将边划分为两种类型：

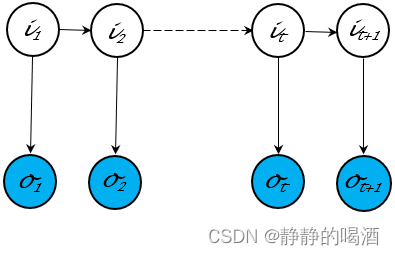
  • 有向图模型($\text{Directed Graphical Model}$)——由有向边构成的模型，也称贝叶斯网络($\text{Batessian Network}$)。代表模型有隐马尔可夫模型($\text{Hidden Markov Model,HMM}$)，其概率图结构表示如下：
    有向图的特点是：能够直接观察出随机变量结点之间的因果关系。仅凭概率图结构就可以描述其联合概率分布的因子分解。相反，有向图内部结点的结构关系比较复杂。共包含三种结构(传送门——贝叶斯网络的结构表示)
    
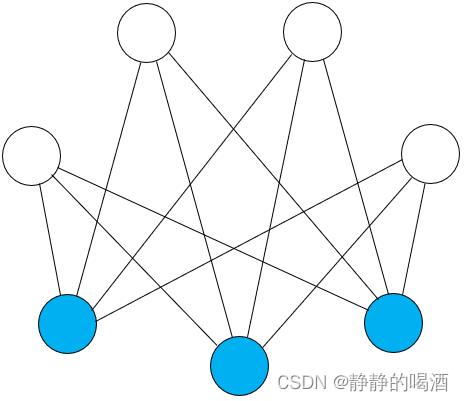
  • 无向图模型($\text{Undirected Graphical Model}$)——由无向边构成的模型，也称马尔可夫随机场($\text{Markov Random Field,MRF}$)。代表模型有受限玻尔兹曼机($\text{Restricted Boltzmann Machine,RBM}$)，其概率图结构表示如下：
    相比于有向图，无向图的特点是：结点内部结构关系简单，但仅能观察到结点之间存在关联关系而不是因果关系。通过极大团、势函数的方式描述联合概率分布(传送门——马尔可夫随机场的结构表示)
    

• 从随机变量结点类型的角度观察，可以将概率图模型分为两种类型：

  • 隐变量模型($\text{Latent Variable Model,LVM}$)：概率图结构中随机变量结点既包含隐变量、也包含观测变量。上面介绍的几种都属于隐变量模型。还有其他模型如$\text{Sigmoid}$信念网络等等。
    隐变量本身是被假设出来的随机变量，它本身可能不存在实际意义。
  • 完全观测变量模型($\text{Fully-Observed Model}$)：与隐变量模型相反，该模型结构中所有随机变量结点均是观测变量，例如朴素贝叶斯分类器($\text{Naive Bayes Classifier}$)：
    这意味着概率图结构中的所有随机变量结点均是有真实意义的。
    

• 从概率图结构的复杂程度角度观察，可以将其划分为：

  • 浅层模型($\text{Shallow Model}$)： 这里的浅层模型是指没有产生随机变量堆叠的现象。也就是说，没有构建新的随机变量去对原有设定的随机变量进行表示。上述所有介绍的模型均属于浅层模型。
    虽然$\text{Sigmoid}$信念网络也存在‘层级现象’，但这种层级现象中的隐变量结点也不属于深度生成模型。
例如：动态模型如隐马尔可夫模型，虽然它的随机变量结点是基于时间、空间角度无限延伸的，但它同样也是浅层模型。
    从浅层模型随机变量结点内部关联关系角度观察，浅层结点内部结点之间关联关系是高度固化的，或者说是稀疏($\text{Sparse}$)的。
    依然使用‘隐马尔可夫模型’举例，由于‘齐次马尔可夫假设’与‘观测独立性假设’的约束，某个隐变量结点只能与‘对应状态的观测变量、下个状态的隐变量’之间存在因果关系。而与其他结点无关。
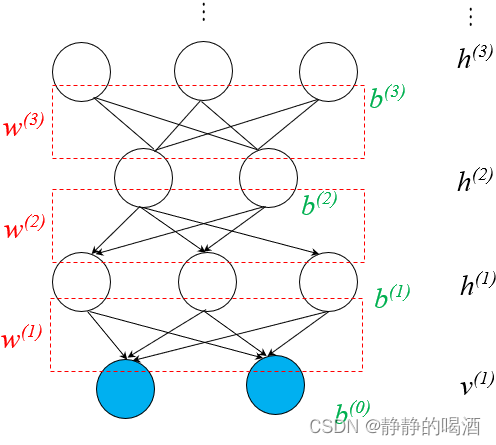
  • 深度生成模型($\text{Deep Generative Model}$)：这里的深度指的是深度学习。与上面描述相反，其主要特征是 假设新的随机变量对原有假设的随机变量进行表示。具有代表性的模型有深度信念网络($\text{Deep Belief Network,DBN}$)：
    相反，深度生成模型内部结构中，层与层之间的关联关系是稠密($\text{Dense}$)的。
    

从概率分布的角度观察生成模型的表示任务

在生成模型综述——生成模型介绍中介绍过，生成模型的关注点均在样本分布自身。那么关于样本分布的概率密度函数$\mathcal{P}(\mathcal{X})$内部的模型参数$\theta$可分为参数化与非参数化两种类型：

• 之前介绍过的绝大多数模型均属于参数化模型($\text{Parameteric Model}$)，可以将模型参数$\theta$看作是未知常量。通过对模型学习得到参数的 解或者是近似解。依然以隐马尔可夫模型为例：
  其中$\pi$表示初始状态$\mathcal{P}(i_1)$的概率分布;$\mathcal{A}$表示状态转移矩阵;$\mathcal{B}$表示发射矩阵。$\pi ,a_{ij},b_j(k)$均属于模型参数。
  λ = ( π , A , B ) { π = ( p 1 , p 2 , ⋯   , p K ) K × 1 T ∑ k = 1 K p k = 1 A = [ a i j ] K × K a i j = P ( i t + 1 = q j ∣ i t = q i ) ; i , j ∈ { 1 , 2 , ⋯   , K } B = [ b j ( k ) ] K × M b j ( k ) = P ( o t = v k ∣ i t = q j ) ; j ∈ { 1 , 2 , ⋯   , K } ; k ∈ { 1 , 2 , ⋯   , M } \begin{aligned} & \lambda = (\pi,\mathcal A,\mathcal B) \\ & \begin{cases} \pi = (p_1,p_2,\cdots,p_{\mathcal K})_{\mathcal K \times 1}^T \quad \sum_{k=1}^{\mathcal K} p_k = 1 \\ \mathcal A = [a_{ij}]_{\mathcal K \times \mathcal K} \quad a_{ij} = \mathcal P(i_{t+1} = q_j \mid i_t = q_i);i,j \in \{1,2,\cdots,\mathcal K\} \\ \mathcal B = [b_j(k)]_{\mathcal K \times \mathcal M} \quad b_j(k) = \mathcal P(o_t = v_k \mid i_t = q_j);j \in \{1,2,\cdots,\mathcal K\};k \in \{1,2,\cdots,\mathcal M\} \end{cases} \end{aligned} ​λ=(π,A,B)⎩ ⎨ ⎧​π=(p1​,p2​,⋯,pK​)K×1T​∑k=1K​pk​=1A=[aij​]K×K​aij​=P(it+1​=qj​∣it​=qi​);i,j∈{1,2,⋯,K}B=[bj​(k)]K×M​bj​(k)=P(ot​=vk​∣it​=qj​);j∈{1,2,⋯,K};k∈{1,2,⋯,M}​​
  再例如玻尔兹曼机($\text{Boltzmann Machine,BM}$)，它的概率密度函数可表示为：
  P ( v , h ) = 1 Z exp ⁡ { − E ( v , h ) } = 1 Z exp ⁡ [ v T W ⋅ h + 1 2 v T L ⋅ v + 1 2 h T J ⋅ h ] \begin{aligned} \mathcal P(v,h) & = \frac{1}{\mathcal Z} \exp \{-\mathbb E(v,h)\} \\ & = \frac{1}{\mathcal Z} \exp \left[v^T \mathcal W \cdot h + \frac{1}{2} v^T \mathcal L \cdot v + \frac{1}{2}h^T \mathcal J \cdot h\right] \end{aligned} P(v,h)​=Z1​exp{−E(v,h)}=Z1​exp[vTW⋅h+21​vTL⋅v+21​hTJ⋅h]​
  对应需要学习的模型参数可表示为：
  其中$\mathcal{W},\mathcal{L},\mathcal{J}$均以矩阵的形式表示。
  θ = { W , L , J } \theta = \{\mathcal W,\mathcal L,\mathcal J\} θ={W,L,J}

• 无参数化模型($\text{Non-Parameteric Model}$)主要有高斯过程($\text{Gaussian Process,GP}$)，由于高斯过程在连续域$\mathcal{T}$内的任意一个时刻均服从高斯分布，因而可以理解为它的模型参数是无限的：
  后续尝试介绍‘狄利克雷过程’~
  $${\xi }_{t_i}\sim \mathcal{N}({\mu }_{t_i},{\Sigma }_{t_i})t_i\in \mathcal{T}$$

除去参数的角度，从是否直接通过关注样本自身分布$\mathcal{P}(\mathcal{X})$对生成模型进行划分：

• 显式概率密度思想($\text{Explict Density}$)：无论是包含隐变量的生成模型如高斯混合模型：
  $$\begin{array}{rl}\mathcal{P}(\mathcal{X})& =\sum _{\mathcal{Z}}\mathcal{P}(\mathcal{X},\mathcal{Z})\\ & =\sum _{\mathcal{Z}}\mathcal{P}(\mathcal{Z})\cdot \mathcal{P}(\mathcal{X}\mid \mathcal{Z})\\ & =\sum _{k=1}^{\mathcal{K}}{p}_k\cdot \mathcal{N}({\mu }_k,{\Sigma }_k)\sum _{k=1}^{\mathcal{K}}{p}_k=1\end{array}$$
  还是完全观测变量模型如朴素贝叶斯分类器：

  • 需要注意的是，由于是监督学习任务，因此这里的$\mathcal{X},\mathcal{Y}$均属于观测变量。因而这里观测变量的概率密度函数是$\mathcal{P}(\mathcal{X},\mathcal{Y})$。以二分类为例：
  • 第一次转换使用‘贝叶斯定理’$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})=\frac{\mathcal{P}(\mathcal{X},\mathcal{Y})}{\mathcal{P}(\mathcal{X})}$由于$\mathcal{P}(\mathcal{X})={\int }_{\mathcal{Y}}\mathcal{P}(\mathcal{X},\mathcal{Y})d\mathcal{Y}$与$\mathcal{Y}$无关，被视作常量。因而有：$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})\propto \mathcal{P}(\mathcal{X},\mathcal{Y})$.
    $$\begin{array}{rl}& \mathcal{P}(\mathcal{Y}=0\mid \mathcal{X})\stackrel{\text{?}}{\iff }\mathcal{P}(\mathcal{Y}=1\mid \mathcal{X})\\ & \propto \mathcal{P}(\mathcal{X},\mathcal{Y}=0)\stackrel{\text{?}}{\iff }\mathcal{P}(\mathcal{X},\mathcal{Y}=1)\\ & \Rightarrow \mathcal{P}(\mathcal{Y}=1)\cdot \mathcal{P}(\mathcal{X}\mid \mathcal{Y}=1)\stackrel{\text{?}}{\iff }\mathcal{P}(\mathcal{Y}=0)\cdot \mathcal{P}(\mathcal{X}\mid \mathcal{Y}=0)\end{array}$$

  它们都属于对样本自身的概率密度函数进行建模。

• 隐式概率密度思想($\text{Implict Density}$)：相比之下，这种思路在建模的过程中，并不直接考虑样本自身分布$\mathcal{P}(\mathcal{X})$。例如样本生成任务中，目标是生成与$\mathcal{P}(\mathcal{X})$相似的幻想粒子，但并不是完全得到$\mathcal{P}(\mathcal{X})$之后才能生成，即便是不知道，也可以生成。例如生成对抗网络($\text{Generative Adversarial Networks,GAN}$)中的生成器部分：
  很明显，生成对抗网络将样本自身概率分布$\mathcal{P}(\mathcal{X})$视作一个复杂函数，使用神经网络的通用逼近定理完成。其输入$\mathcal{Z}$仅是一个简单分布，而该函数描述的是关于$\mathcal{X}$的后验概率$\mathcal{P}(\mathcal{X}\mid \mathcal{Z})$.
  $$\mathcal{X}=\mathcal{G}(\mathcal{Z},{\theta }_{gene})\Rightarrow \mathcal{P}(\mathcal{X}\mid \mathcal{Z})$$

生成模型的推断任务

关于生成模型推断任务，可以划分为：

• 容易求解($\text{Tractable}$)的。例如受限玻尔兹曼机的随机变量后验概率的推断任务：
  既然是推断任务，模型内部参数均已确定。其中$w_{li}$表示隐变量$h_l$和观测变量$v_i$的权重信息;$c_l$表示偏置信息。
  $$\mathcal{P}(h_l\mid v)=\{\begin{array}{l}\text{Sigmoid}({\sum }_{i=1}^n{\mathcal{W}}_{li}\cdot v_i+c_l)h_l=1\\ 1-\text{Sigmoid}({\sum }_{i=1}^n{\mathcal{W}}_{li}\cdot v_i+c_l)h_l=0\end{array}$$
  由于受限玻尔兹曼机的特殊结构假设，可以通过$\text{Sigmoid}$函数准确描述变量的后验信息。
• 难求解，计算代价极大($\text{Intractable}$)的。如积分难问题：
  $$\begin{array}{rl}\mathcal{P}(\mathcal{X})& ={\int }_{\mathcal{Z}}\mathcal{P}(\mathcal{X},\mathcal{Z})d\mathcal{Z}\\ & ={\int }_{\mathcal{Z}}\mathcal{P}(\mathcal{X}\mid \mathcal{Z})\cdot \mathcal{P}(\mathcal{Z})d\mathcal{Z}\\ & ={\int }_{z_1}\cdots {\int }_{z_{\mathcal{K}}}\mathcal{P}(\mathcal{X}\mid \mathcal{Z})\cdot \mathcal{P}(\mathcal{Z})d{z}_1,\cdots ,z_{\mathcal{K}}\end{array}$$

生成模型的学习任务

关于生成模型参数的学习任务主要使用极大似然估计($\text{Maximum Likelihood Estimate,MLE}$)。因而可划分为：

• 基于极大似然估计的模型($\text{Likelihood-based Model}$)：实际上，绝大多数模型均使用的极大似然估计方法。如以受限玻尔兹曼机为代表的能量模型($\text{Energy Model}$)：
  能量模型参数的学习思想是：基于极大似然估计，求解能量模型的对数似然梯度，最后使用‘梯度上升法’进行近似求解。
  log ⁡ P ( v ; θ ) = log ⁡ [ 1 Z ∑ h exp ⁡ { − E [ h , v ] } ] = log ⁡ [ ∑ h exp ⁡ { − E [ h , v ] } ] − log ⁡ [ ∑ h , v exp ⁡ { − E [ h , v ] } ] ∇ θ [ log ⁡ P ( v ; θ ) ] = ∑ h ( i ) , v ( i ) { P ( h ( i ) , v ( i ) ) ⋅ ∂ ∂ θ [ E ( h ( i ) , v ( i ) ) ] } − ∑ h ( i ) { P ( h ( i ) ∣ v ( i ) ) ⋅ ∂ ∂ θ [ E ( h ( i ) , v ( i ) ) ] } θ ( t + 1 ) ⇐ θ ( t ) + η ⋅ 1 N ∑ v ∈ V ∇ θ [ log ⁡ P ( v ; θ ) ] \begin{aligned} \log \mathcal P(v;\theta) & = \log \left[\frac{1}{\mathcal Z} \sum_{h} \exp \{- \mathbb E[h,v]\}\right] \\ & = \log \left[\sum_{h} \exp \{-\mathbb E[h,v]\}\right] - \log \left[\sum_{h,v} \exp \{-\mathbb E[h,v]\}\right] \\ \nabla_{\theta} \left[\log \mathcal P(v;\theta)\right] & = \sum_{h^{(i)},v^{(i)}} \left\{\mathcal P(h^{(i)},v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} - \sum_{h^{(i)}} \left\{\mathcal P(h^{(i)} \mid v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \\ \theta^{(t+1)} & \Leftarrow \theta^{(t)} + \eta \cdot \frac{1}{N} \sum_{v \in \mathcal V}\nabla_{\theta} \left[\log \mathcal P(v;\theta)\right] \end{aligned} logP(v;θ)∇θ​[logP(v;θ)]θ(t+1)​=log[Z1​h∑​exp{−E[h,v]}]=log[h∑​exp{−E[h,v]}]−log ​h,v∑​exp{−E[h,v]} ​=h(i),v(i)∑​{P(h(i),v(i))⋅∂θ∂​[E(h(i),v(i))]}−h(i)∑​{P(h(i)∣v(i))⋅∂θ∂​[E(h(i),v(i))]}⇐θ(t)+η⋅N1​v∈V∑​∇θ​[logP(v;θ)]​
• 与极大似然估计无关的模型($\text{Likelihood-free Model}$)：最典型的模型依然是生成对抗网络。它使用的是对抗学习思路：
  它对判别模型$\mathcal{D}(\mathcal{X};{\theta }_d)$进行建模，其策略可表示为：
  min ⁡ G max ⁡ D { E x ∼ P d a t a [ log ⁡ D ( x ; θ d ) ] + E Z ∼ P ( Z ) [ log ⁡ { 1 − D [ G ( Z ; θ g e n e ) ; θ d ] } ] } \mathop{\min}\limits_{\mathcal G} \mathop{\max}\limits_{\mathcal D} \{\mathbb E_{x \sim \mathcal P_{data}} \left[\log \mathcal D(x;\theta_d)\right] + \mathbb E_{\mathcal Z \sim \mathcal P(\mathcal Z)} \left[\log \{1 - \mathcal D[\mathcal G(\mathcal Z;\theta_{gene});\theta_d]\}\right]\} Gmin​Dmax​{Ex∼Pdata​​[logD(x;θd​)]+EZ∼P(Z)​[log{1−D[G(Z;θgene​);θd​]}]}

至此，关于生成模型从表示、推断、学习三个任务的区别介绍结束。

相关参考：
生成模型3-表示&推断&学习