分类预测 |Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测

分类效果

基本介绍

Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测（完整源码和数据）
1.Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测；
2.输入数据为多特征分类数据，即数据输入12个特征，输出分四类；
3.运行环境Matlab2018及以上,运行MainSSA_RF即可，其余为函数文件无需运行,所有程序放在一个文件夹,data为数据集；
4.麻雀算法优化随机森林树木棵树和森林深度，输入12个特征，分四类，可视化展示分类准确率，模型对比输出。

模型描述

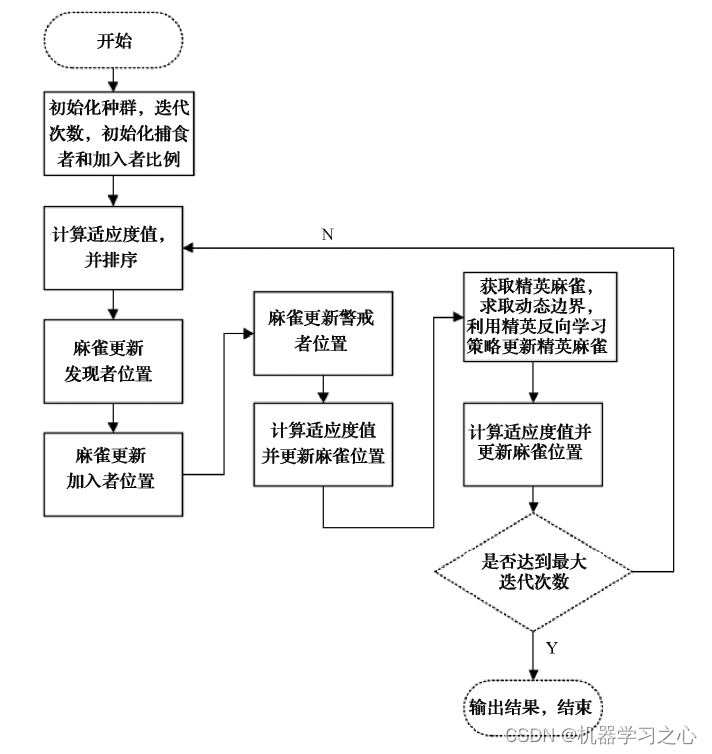
• 麻雀算法

SSA是于2020年提出的,比较新颖,具有寻优能力强,收敛速度快的优点。
首先,对种群初始化。设有n只麻雀组成的种群表示为:

在SSA 中,一部分麻雀作为发现者为种群搜索食物探路。种群中60%的个体作为加入者,依据发现者提供的觅食方向觅食,并且发现者和加入者的身份是动态变化的。最后剩下个体作为警戒者,观察食物周围环境是否有危险,一旦发现危险,立刻发出信号,所有麻雀作出反捕食行为。在每次迭代的过程中,发现者的位置更新描述，如下:

• 随机森林

集成学习常见的独立学习器生成方式有串行序列生成(Boosting)和并行序列生成(Bagging)两种,RF在思想上可以看作是Bagging的改进假设有一个样本集D = {(x1,y1),(x2,y2),…,(x3,y3)},通过自然采样法抽取若干小样本集1,D2,…,DK作为输入训练出C1,C2,…,CK 共K 个弱学习器。再把测试数据导入训练好的弱学习器进行预测分类,通过计算K个弱学习器预测结果的平均值得到最终决策结果。

程序设计

• 完整程序和数据下载方式1：同等价值程序兑换；
• 完整程序和数据下载方式2：Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测

%_________________________________________________________________________%
% 麻雀优化算法             %
%_________________________________________________________________________%
function [Best_pos,Best_score,curve]=SSA(pop,Max_iter,lb,ub,dim,fobj)

ST = 0.7;%预警值
PD = 0.4;%发现者的比列，剩下的是加入者0.7
SD = 0.2;%意识到有危险麻雀的比重

PDNumber = round(pop*PD); %发现者数量
SDNumber = round(SD*PD);%意识到有危险麻雀数量

%种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
%计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
   fitness(i) =  fobj(X(i,:));
end
[fitness, index]= sort(fitness);%升排序
BestF = fitness(1);
WorstF = fitness(end);
GBestF = fitness(1);%全局最优适应度值
for i = 1:pop
    X(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:);%全局最优位置
X_new = X;
for i = 1: Max_iter
    
    disp(['第',num2str(i),'次迭代'])
    BestF = fitness(1);
    WorstF = fitness(end);

    
    R2 = rand(1);
   for j = 1:PDNumber
      if(R2<ST)
          X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));
      else
          X_new(j,:) = X(j,:) + randn()*ones(1,dim);
      end     
   end
   for j = PDNumber+1:pop
%        if(j>(pop/2))
        if(j>(pop - PDNumber)/2 + PDNumber)
          X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);
        else
          %产生-1，1的随机数
          A = ones(1,dim);
          for a = 1:dim
            if(rand()>0.5)
                A(a) = -1;
            end
          end 
          AA = A'*inv(A*A');     
          X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';
       end
   end
   Temp = randperm(pop);
   SDchooseIndex = Temp(1:SDNumber); 
   for j = 1:SDNumber
       if(fitness(SDchooseIndex(j))>BestF)
           X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));
       elseif(fitness(SDchooseIndex(j))== BestF)
           K = 2*rand() -1;
           X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));
       end
   end
  %边界控制
   for j = 1:pop
       for a = 1: dim
           if length(ub)>1
               if(X_new(j,a)>ub(a))
                   X_new(j,a) =ub(a);
               end
               if(X_new(j,a)<lb(a))
                   X_new(j,a) =lb(a);
               end
           else
                if(X_new(j,a)>ub)
                   X_new(j,a) =ub;
               end
               if(X_new(j,a)<lb)
                   X_new(j,a) =lb;
               end
           end
       end
   end 
   %更新位置
   for j=1:pop
     fitness_new(j) = fobj(X_new(j,:));
   end
   for j = 1:pop
    if(fitness_new(j) < GBestF)
       GBestF = fitness_new(j);
        GBestX = X_new(j,:);   
    end
   end
   X = X_new;
   fitness = fitness_new;
    %排序更新
   [fitness, index]= sort(fitness);%排序
   BestF = fitness(1);
   WorstF = fitness(end);
   for j = 1:pop
      X(j,:) = X(index(j),:);
   end
   curve(i) = GBestF;
    disp(['current iteration is: ',num2str(i), ', best fitness is: ', num2str(GBestF)]);
end
Best_pos =GBestX;  %全局最优位置 K  Alpha值组合
Best_score = curve(end);%全局最优适应度值  熵值最小
end

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128589064?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5502