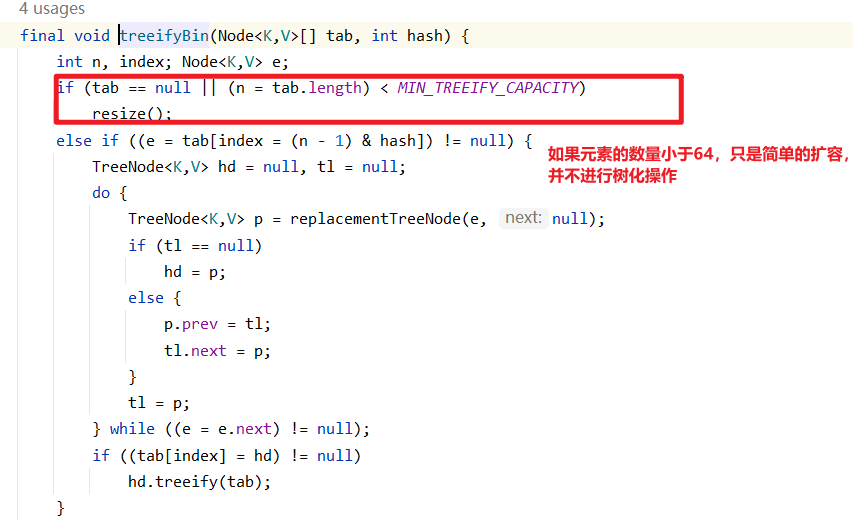
表格数据

表格中的每一行都独立于其他行，他们的顺序页没有任何关系。并且，没有提供有关行之前和行之后的列编码信息。

表格类型的数据是指通过表格的形式表示的数据，它以行和列的方式组织数据。表格中的每一行代表一个数据项，每一列代表数据项的一个属性。

表格类型的数据具有以下特点：

• 结构化：表格数据是结构化的，每一列代表相同类型的数据，易于整理和分析。

• 可视化：表格数据可以通过图形或图表的形式进行可视化，方便了数据的可视化分析。

• 易于管理：表格数据可以使用表格处理软件（如 Microsoft Excel）进行管理和分析，使用方便。

表格类型的数据的主要优势在于：

• 可读性强：表格数据以行和列的形式组织，易于理解。

• 数据分析方便：表格数据提供了丰富的分析功能，如排序、筛选、计算等，方便了数据分析。

• 数据共享方便：表格数据可以通过电子邮件或云端存储等方式进行共享，方便了数据共享。

时间序列数据

时间序列数据是指随着时间的推移而收集的数据。它们通常以时间为主题，可以是每天、每周、每月或每年的数据。例如，股票价格、气温、销售额、交通流量等都是时间序列数据。这些数据通常用于趋势分析、预测和模型构建。

这里我们通过将时间序列数据转换为张量，来作为我们的模型的输入。本次选取的是：华盛顿特区自行车共享系统中的数据，报告了2011年至2012年之间首都自行车共享系统中租用自行车的每小时计数以及相应的天气和季节性信息。

我们的目的是获取平面2D数据集并将其转换为3D数据集

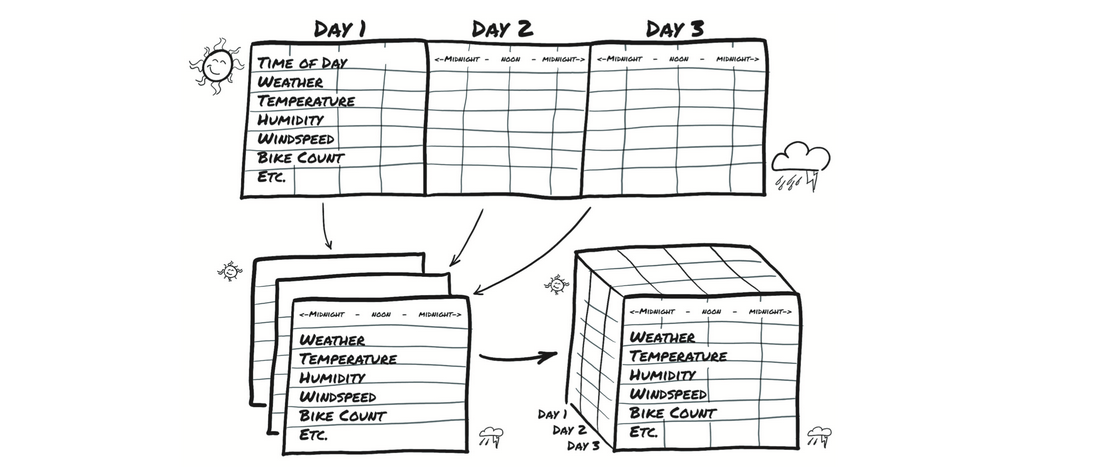
在源数据中，每一行是单独一个小时的数据，我们想改变行-小时的组织方式，这样你就可以使一个轴以天的速度增加，而另一个轴代表一天中的小时（与日期无关）。第三个轴每一列数据不同（天气，温度等）。这样就变成3维的一个数据。

使用numpy加载数据

bikes_numpy = np.loadtxt("./hour-fixed.csv",
                         dtype=np.float32,
                         delimiter=",",
                         skiprows=1,
                         converters={1: lambda x: float(x[8:10])})
bikes = torch.from_numpy(bikes_numpy) 
bikes

这段代码使用了 Numpy 库中的 loadtxt 函数来读取 “./hour-fixed.csv” 文件，并将其转换为 float32 类型的数组，以逗号分隔，跳过第 1 行，并使用 converters 参数将第 1 列的数据转换为从第 8 个字符开始的两个字符的浮点数。

然后，使用 PyTorch 中的 from_numpy 函数将 Numpy 数组转换为 PyTorch 张量。

最后，bikes 变量是 PyTorch 张量。

输出

tensor([[1.0000e+00, 1.0000e+00,  ..., 1.3000e+01, 1.6000e+01],         
        [2.0000e+00, 1.0000e+00,  ..., 3.2000e+01, 4.0000e+01],         
        ...,         
        [1.7378e+04, 3.1000e+01,  ..., 4.8000e+01, 6.1000e+01],         
        [1.7379e+04, 3.1000e+01,  ..., 3.7000e+01, 4.9000e+01]])

数据标签：

instant      # index of record #索引记录
day          # day of month #一个月中的某天
season       # season (1: spring, 2: summer, 3: fall, 4: winter) #季节（1：春天，2：夏天，3：秋天，4：冬天）
yr           # year (0: 2011, 1: 2012) #年份
mnth         # month (1 to 12) #月
hr           # hour (0 to 23) #小时
holiday      # holiday status #假期状态
weekday      # day of the week #一周的某天
workingday   # working day status #工作状态
weathersit   # weather situation #天气情况             
                         # (1: clear, 2:mist, 3: light rain/snow, 4: heavy rain/snow) #1：晴，2：薄雾，3：小雨/雪，4：大雨/雪
temp         # temperature in C #摄氏温度
atemp        # perceived temperature in C #感知温度（摄氏度）
hum          # humidity #湿度
windspeed    # windspeed #风速
casual       # number of causal users #因果用户数
registered   # number of registered users #注册用户数
cnt          # count of rental bikes #出租自行车数

在此类的时间序列数据集中，行表示连续的时间点：按其排序来制定维度。当然，你可以将每一行视为独立行，并尝试根据例如一天中的特定时间来预测循环的自行车数量，而不管之前发生的事情如何。

但是，这种排序使你有机会利用因果关系去跨越时间。例如，你可以根据先前下雨的情况来预测一次自行车的骑行次数。暂且将你的注意力放在学习如何将自行车共享数据集转化为你的神经网络可以以固定大小提取的数据块。

这个神经网络模型需要查看每种数据的值序列，例如乘车次数，一天中的时间，温度和天气状况，因此N个并行的大小为C的并行序列。C代表通道（channel），在神经网络中，它与此处所用的一维数据列（column）相同。 N维代表时间轴，这里是每小时输入一次。

你可能希望在更长的收集期内（例如天）拆分2年数据集。以这种方式，你将获得N个样本数（number of samples），样本由长度为L的C个序列的集合。换句话说，你的时间序列数据集是维度为3的张量，形状为N x C xL。C仍然是 17个通道，而L则是一天中的24个小时通道。

没有必要特别说明为什么我们必须使用24小时这一时间段，尽管一般的日常的生活节奏可能会给我们提供可用于预测的模式。如果需要，我们可以改为使用7 * 24 = 168个小时块来按周划分数据集。

这就是为啥我们可以将一个一维的数据变成2维或者3维的数据，可以通过维度转换将数据变成一个立体多维度的数据。

第一列是索引（数据的全局顺序）；第二个是日期；第六个是一天中的时间点。你拥有可以创建行驶计数和其他变量等日常序列数据集所需的一切。一般情况下你的数据集已经排好序，但是如果一旦没有排序，你可以在其上使用torch.sort进行适当排序。

要获取每日工作时间数据集，你要做的就是每隔24小时查看同一个张量。看看你的自行车（bikes）张量的形状和步幅：

bikes.shape, bikes.stride()

这里的步长也就是为什么前面我们花了大量的例子是时间来学习它的概念，因为在现实的处理中它也是比较多的一种方法。

(torch.Size([17520, 17]), (17, 1))

这是17,520小时，共17列。现在将数据重新排列为具有三个轴（日期，小时，然后是17列）。

daily_bikes = bikes.view(-1, 24, bikes.shape[1]) 
daily_bikes.shape, daily_bikes.stride()

首先定义了一个变量 daily_bikes，它是对变量 bikes 的视图（view）。这个视图操作实际上是对 bikes 进行重新 reshape（重塑）的操作，将其变为三维张量，形状为 (-1, 24, bikes.shape[1])。

其中，-1 表示的是第一维的大小是根据其他维度的大小自动计算出来的，24 表示第二维的大小为 24，bikes.shape[1] 表示第三维的大小是 bikes 的第二维的大小。

接下来，输出 daily_bikes 的形状（shape）和步长（stride）。步长（stride）是指在内存中相邻元素间的存储间隔，即元素间的距离。

(torch.Size([730, 24, 17]), (408, 17, 1))

bikes.shape [1]为17，它是自行车（bikes）张量中的列数

在张量上调用视图方法（view）返回一个新的张量，该张量可以更改维数和步幅信息，而无需更改存储。

结果，你可以以零成本重新布置张量因为根本没有数据被复制。你的视图（view）调用要求你为返回的张量提供新的形状。将-1用作占位符是为了“但是考虑到其他维度和元素的原始数量，还剩下很多索引”。

记住在这种情况下，存储（Storage）是连续的数字的线性容器——浮点数。你的自行车（bikes）张量在相应的存储中逐行存储，这一点已通过早期对bikes.stride()的调用输出确认。

对于daily_bikes，步幅告诉你沿小时维度（第二个）前进1个位置需要你将存储（或一组列）中的位置前进17个位置，而沿日期维度（第一个）前进则需要你在时间24小时中前进等于行长度的元素数（此处为408，即17 * 24）。

最右边的维度是原始数据集中的列数。在中间维度中，你将时间分为24个连续小时的块。换句话说，你现在每天有C个通道的N个L小时的序列。为了获得你所需的NxCxL顺序，你需要转置张量：

daily_bikes = daily_bikes.transpose(1, 2) 
daily_bikes.shape, daily_bikes.stride()

(torch.Size([730, 17, 24]), (408, 1, 17))

天气状况变量是有序数。实际上，它有4个等级：1表示最佳天气，而4表示最坏的天气。你可以将此变量视为分类变量，其级别解释为标签或者连续标签。

如果你选择分类，则将变量转换为独热编码的向量，并将列与数据集连接起来。为了使你的数据渲染更容易，现在暂时限制为第一天。首先，初始化一个零填充矩阵，其行数等于一天中的小时数，列数等于天气等级的数:

first_day = bikes[:24].long() 
weather_onehot = torch.zeros(first_day.shape[0], 4) 
first_day[:,9]

首先，取出 bikes 列表的前 24 行并转化为长整型：

复制 first_day = bikes[:24].long()

接着，创建一个用于保存天气类型的 one-hot 编码的张量：

复制 weather_onehot = torch.zeros(first_day.shape[0], 4)

最后，取出第一天数据中第 9 列的数据：

复制 first_day[:, 9]

tensor([1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 2, 2, 2, 2])

然后根据每一行的相应的等级将它们分散到我们的矩阵中。请记住，在之前需要使用取消压缩（unsqueeze）来添加单例尺寸：

weather_onehot.scatter_(
  dim=1,
  index=first_day[:,9].unsqueeze(1) - 1,
  value=1.0)

tensor([[1., 0., 0., 0.],
        [1., 0., 0., 0.],
        ...,
        [0., 1., 0., 0.],
        [0., 1., 0., 0.]])

这一天从1级天气开始到2级天气结束，所以这似乎是正确的。

最后，使用cat函数将矩阵连接到原始数据集。看你的第一个结果：

torch.cat((bikes[:24], weather_onehot), 1)[:1]

表示将前 24 行的 bikes 数据和 weather_onehot 数据在第一维上进行拼接，然后取出第一行数据。

tensor([[ 1.0000,  1.0000,  1.0000,  0.0000,  1.0000,  0.0000,  0.0000,  6.0000,
          0.0000,  1.0000,  0.2400,  0.2879,  0.8100,  0.0000,  3.0000, 13.0000,
          16.0000,  1.0000,  0.0000,  0.0000,  0.0000]])

在这里，你指定了原始自行车（bikes）数据集和独热编码的天气情况矩阵，这些矩阵将沿列维（例如1）连接在一起。换句话说，将两个数据集的列堆叠在一起，或者将新的独热编码列追加到原始数据集。为了使cat成功，张量必须与其他维度（行维度在这种情况也想通）有相同的大小。

请注意，你最后的新四列分别是1,0,0,0——这正是你所期望的天气等级1。

你也可以使用重新排列的daily_bikes张量完成相同的操作。请记住，它的形状为（B,C,L），其中L=24。首先创建零张量，有相同的B和L，但增加的列数与C：

daily_weather_onehot = torch.zeros(daily_bikes.shape[0], 4,
daily_bikes.shape[2]) 
daily_weather_onehot.shape

torch.Size([730, 4, 24])

然后将独热编码散布到C维中的张量中。由于操作是在原地执行的，因此仅张量的内容会更改：

daily_weather_onehot.scatter_(1, daily_bikes[:,9,:].long().unsqueeze(1) - 1,1.0) 
daily_weather_onehot.shape

将daily_bikes第9列的值作为索引，将daily_weather_onehot中这些索引对应的值设置为1.0

torch.Size([730, 4, 24])

沿C维度连接：

daily_bikes = torch.cat((daily_bikes, daily_weather_onehot), dim=1)

这种方法并不是处理天气情况变量的唯一方法。实际上，其标签具有序数关系因此你可以暂时认为它们是连续变量的特殊值。你可以转换变量，使其从0.0到1.0运行：

daily_bikes[:, 9, :] = (daily_bikes[:, 9, :] - 1.0) / 3.0

重新缩放变量为[0.0,1.0]区间或[-1.0,1.0]区间是你需要对所有的变量进行的操作，例如温度（temperature）（数据集中的第10列）。

方法1

temp = daily_bikes[:, 10, :]
temp_min = torch.min(temp)
temp_max = torch.max(temp)
daily_bikes[:, 10, :] = (daily_bikes[:, 10, :] - temp_min) / (temp_max -
     temp_min)

方法2

temp = daily_bikes[:, 10, :] 
daily_bikes[:, 10, :] = (daily_bikes[:, 10, :] - torch.mean(temp)) / 
     torch.std(temp)

变量的平均值为零并且标准差为零。如果取自高斯分布，则68％的样本将位于[-1.0,1.0]区间。

每文一语

有时候无聊也会惊醒